《機械》〈回転機〉[H22:問5]同期発電機のリアクタンスに関する空欄穴埋問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，同期発電機のリアクタンスに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な語句又は式を解答群の中から選びなさい。

無負荷で電圧を誘起している同期発電機の端子を三相短絡させたとき，短絡初期に大きな短絡電流が流れ，時間の経過とともに次第に減少して持続する短絡電流になる。初期の短絡電流の大きさは，回転子回路に制動作用を生じるものがない場合は直軸過渡リアクタンス\( \ X_{\mathrm {d}}^{\prime } \ \)によって支配されるが，制動作用を生じるものがある場合は直軸初期過渡リアクタンス\( \ X_{\mathrm {d}}^{\prime \prime } \ \)によって支配される。

同期リアクタンスを直軸同期リアクタンス\( \ X_{\mathrm {d}} \ \)と横軸同期リアクタンス\( \ X_{\mathrm {q}} \ \)とに分けて取り扱う場合，円筒形同期発電機のときには飽和の影響を無視すると\( \ X_{\mathrm {d}} \ \)と\( \ X_{\mathrm {q}} \ \)との大きさの関係は，\( \ \fbox {　 （１） 　} \ \)となるが，突極形同期発電機のときには直軸方向と横軸方向の\( \ \fbox {　 （２） 　} \ \)抵抗の大きさが異なるので\( \ \fbox {　 （３） 　} \ \)となる。

同期発電機に不平衡電流が流れる場合，不平衡電流を対称分に分けて取り扱うことができる。逆相電流に対する逆相リアクタンス\( \ X_{\mathrm {2}} \ \)は近似的に\( \ \fbox {　 （４） 　} \ \)として計算される。また，零相電流に対する零相リアクタンス\( \ X_{\mathrm {0}} \ \)の大きさを他のリアクタンスとの関係で表せば\( \ \fbox {　 （５） 　} \ \)とみなせる。

（注）\( \ X_{\mathrm {d}} \ \)：直軸同期リアクタンス　　　　 \( \ X_{\mathrm {q}} \ \)：横軸同期リアクタンス
　　　\( \ X_{\mathrm {d}}^{\prime } \ \)：直軸過渡リアクタンス　　　　\( \ X_{\mathrm {d}}^{\prime \prime } \ \)：直軸初期過渡リアクタンス
　　　\( \ X_{\mathrm {q}}^{\prime \prime } \ \)：横軸初期過渡リアクタンス　　 \( \ X_{\mathrm {ℓ}} \ \)：電機子漏れリアクタンス
　　　\( \ X_{\mathrm {2}} \ \)：逆相リアクタンス　　　　　　 \( \ X_{\mathrm {0}} \ \)：零相リアクタンス

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　X_{\mathrm {d}}≒2X_{\mathrm {q}}　　　　　&（ロ）&　\frac {X_{\mathrm {d}}^{\prime \prime }+X_{\mathrm {q}}^{\prime \prime }}{2}　　　　　&（ハ）&　\frac {X_{\mathrm {d}}^{\prime \prime }}{2} \\[ 5pt ] &（ニ）&　磁　気　　　　　&（ホ）&　飽　和　　　　　&（ヘ）&　X_{\mathrm {d}}=X_{\mathrm {q}}-X_{\mathrm {ℓ}} \\[ 5pt ] &（ト）&　X_{\mathrm {d}}＜\frac {X_{\mathrm {q}}}{2}　　　　　&（チ）&　X_{\mathrm {0}}＞X_{\mathrm {q}}^{\prime \prime }　　　　　&（リ）&　X_{\mathrm {0}}≒\sqrt {3}X_{\mathrm {ℓ}} \\[ 5pt ] &（ヌ）&　X_{\mathrm {d}}＞X_{\mathrm {q}}　　　　　&（ル）&　X_{\mathrm {0}}＜X_{\mathrm {ℓ}}　　　　　　　&（ヲ）&　X_{\mathrm {d}}≒X_{\mathrm {q}} \\[ 5pt ] &（ワ）&　\frac {X_{\mathrm {d}}^{\prime \prime }+X_{\mathrm {ℓ}}}{\sqrt {2}}　　　　　&（カ）&　X_{\mathrm {d}}＜X_{\mathrm {q}}　　　　　&（ヨ）&　電機子 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

同期発電機のリアクタンスに関する問題です。
かなり専門性の高い受験生にとっては厳しい問題であったかと思います。
近年の出題傾向からも再出題の可能性は低いかもしれませんが，\( \ \mathrm {d} \ \)軸と\( \ \mathrm {q} \ \)軸の概念等は理解しておくと良いでしょう。

1.同期機の\( \ \mathrm {d} \ \)軸成分等価回路と\( \ \mathrm {q} \ \)軸成分等価回路
同期機の回転子の磁極と同じ向きの軸を直軸(\( \ \mathrm {d} \ \)軸)，磁極と直角の向きの軸を横軸(\( \ \mathrm {q} \ \)軸)としたときの等価回路は図2及び図3のようになります。

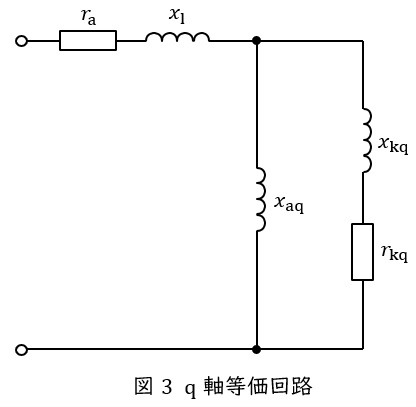
\( \ r_{\mathrm {a}} \ \)：電機子巻線抵抗，\( \ x_{\mathrm {l}} \ \)：電機子巻線漏れリアクタンス
\( \ x_{\mathrm {ad}}，x_{\mathrm {aq}} \ \)：電機子反作用リアクタンス，　\( \ r_{\mathrm {fd}} \ \)：界磁巻線抵抗
\( \ x_{\mathrm {fd}} \ \)：界磁巻線リアクタンス，　\( \ r_{\mathrm {kd}}，r_{\mathrm {kq}} \ \)：制動巻線抵抗
\( \ x_{\mathrm {kd}}，x_{\mathrm {kq}} \ \)：制動巻線リアクタンス

2.突極形同期発電機の直軸同期リアクタンスと横軸同期リアクタンスの違い
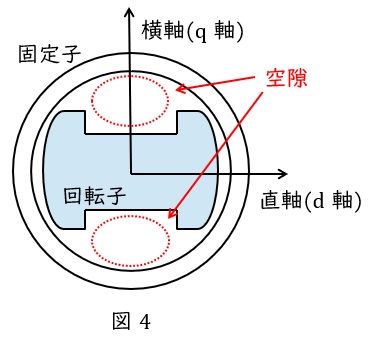
円筒形同期発電機は直軸方向と横軸方向の透磁率の違いはほとんどありませんが，突極形同期発電機は図4に示すように，横軸方向に空隙がある分横軸方向の方が透磁率は小さくなります。
透磁率が小さいと磁気抵抗\( \ \displaystyle R_{\mathrm {m}}\left( =\frac {l}{\mu S}\right) \ \)が大きくなります。
磁気抵抗\( \ \displaystyle R_{\mathrm {m}} \ \)が大きいと，インダクタンス\( \ \displaystyle L\left( =\frac {N^{2}}{R_{\mathrm {m}}}\right) \ \)は小さくなります。
よって，突極形同期発電機においては直軸同期リアクタンス\( \ X_{\mathrm {d}} \ \)の方が横軸同期リアクタンス \( \ X_{\mathrm {q}} \ \)より大きくなります。

【解答】

(1)解答：ヲ
題意より解答候補は，（イ）\( \ X_{\mathrm {d}}≒2X_{\mathrm {q}} \ \)，（ヘ）\( \ X_{\mathrm {d}}=X_{\mathrm {q}}-X_{\mathrm {ℓ}} \ \)，（ト）\( \ \displaystyle X_{\mathrm {d}}＜\frac {X_{\mathrm {q}}}{2} \ \)，（ヌ）\( \ \displaystyle X_{\mathrm {d}}＞X_{\mathrm {q}} \ \)，（ヲ）\( \ \displaystyle X_{\mathrm {d}}≒X_{\mathrm {q}} \ \)，（カ）\( \ \displaystyle X_{\mathrm {d}}＜X_{\mathrm {q}} \ \)，になると思います。
ワンポイント解説「2.突極形同期発電機の直軸同期リアクタンスと横軸同期リアクタンスの違い」の通り，円筒形同期発電機においては\( \ \displaystyle X_{\mathrm {d}}≒X_{\mathrm {q}} \ \)となります。

(2)解答：ニ
題意より解答候補は，（ニ）磁気，（ホ）飽和，（ヨ）電機子，になると思います。
ワンポイント解説「2.突極形同期発電機の直軸同期リアクタンスと横軸同期リアクタンスの違い」の通り，突極形同期発電機は直軸方向と横軸方向の磁気抵抗の大きさが異なります。

(3)解答：ヌ
題意より解答候補は，（イ）\( \ X_{\mathrm {d}}≒2X_{\mathrm {q}} \ \)，（ヘ）\( \ X_{\mathrm {d}}=X_{\mathrm {q}}-X_{\mathrm {ℓ}} \ \)，（ト）\( \ \displaystyle X_{\mathrm {d}}＜\frac {X_{\mathrm {q}}}{2} \ \)，（ヌ）\( \ \displaystyle X_{\mathrm {d}}＞X_{\mathrm {q}} \ \)，（ヲ）\( \ \displaystyle X_{\mathrm {d}}≒X_{\mathrm {q}} \ \)，（カ）\( \ \displaystyle X_{\mathrm {d}}＜X_{\mathrm {q}} \ \)，になると思います。
ワンポイント解説「2.突極形同期発電機の直軸同期リアクタンスと横軸同期リアクタンスの違い」の通り，突極形同期発電機においては\( \ \displaystyle X_{\mathrm {d}}＞X_{\mathrm {q}} \ \)となります。

(4)解答：ロ
題意より解答候補は，（ロ）\( \ \displaystyle \frac {X_{\mathrm {d}}^{\prime \prime }+X_{\mathrm {q}}^{\prime \prime }}{2} \ \)，（ハ）\( \ \displaystyle \frac {X_{\mathrm {d}}^{\prime \prime }}{2} \ \)，（ワ）\( \ \displaystyle \frac {X_{\mathrm {d}}^{\prime \prime }+X_{\mathrm {ℓ}}}{\sqrt {2}} \ \)，になると思います。
同期発電機の逆相電流に対する逆相リアクタンスは近似的に\( \ \displaystyle \frac {X_{\mathrm {d}}^{\prime \prime }+X_{\mathrm {q}}^{\prime \prime }}{2} \ \)で求められます。

(5)解答：ル
題意より解答候補は，（チ）\( \ X_{\mathrm {0}}＞X_{\mathrm {q}}^{\prime \prime } \ \)，（リ）\( \ X_{\mathrm {0}}≒\sqrt {3}X_{\mathrm {ℓ}} \ \)，（ル）\( \ X_{\mathrm {0}}＜X_{\mathrm {ℓ}} \ \)，になると思います。
零相電流に対する零相リアクタンス\( \ X_{\mathrm {0}} \ \)の大きさは電機子漏れリアクタンスよりも小さく\( \ X_{\mathrm {0}}＜X_{\mathrm {ℓ}} \ \)となります。