Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式,数値又は図を解答群の中から選び,その記号をマークシートに記入しなさい。
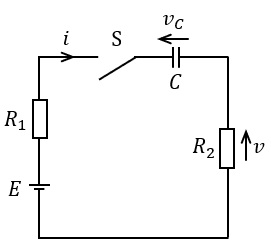
図のように,抵抗\( \ R_{1} \ \),\( \ R_{2} \ \),静電容量\( \ C \ \)及び電圧源\( \ E \ \)を接続した回路がある。この回路における抵抗\( \ R_{2} \ \)の電圧\( \ v \ \)及び静電容量\( \ C \ \)の電圧\( \ v_{C} \ \)の時間的変化を求めたい。
時間\( \ t<0 \ \)ではスイッチ\( \ \mathrm {S} \ \)は開放状態にあり,静電容量\( \ C \ \)の電圧\( \ v_{C} \ \)は\( \ V_{0} \ \)である。ただし,\( \ 0 < V_{0} < E \ \)である。
時刻\( \ t=0 \ \)において,スイッチ\( \ \mathrm {S} \ \)を閉じた。
回路に流れる電流を\( \ i \ \)とすると,抵抗\( \ R_{2} \ \)の電圧\( \ v \ \)は,
\[
\begin{eqnarray}
v&=&R_{2}i ・・・・・・・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
である。
時間\( \ t>0 \ \)における\( \ i \ \)の時間的変化を求める回路方程式は次式となる。
\[
\begin{eqnarray}
R_{1}i+ \ \fbox { (1) } \ +R_{2}i&=&E ・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
①,②式と初期条件より,\( \ v \ \)は次式で表される。
\[
\begin{eqnarray}
v&=& \ \fbox { (2) } \ \times e^{\displaystyle \ \fbox { (3) } \ } \ ・・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
したがって,時間が十分に経過すると\( \ v \ \)は\( \ \fbox { (4) } \ \)に近づく。
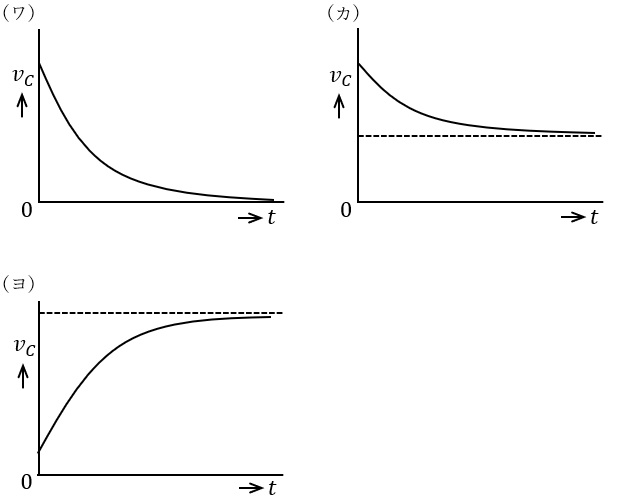
このことを考慮すると,静電容量\( \ C \ \)の電圧\( \ v_{C} \ \)の時間的変化を表す概略図は\( \ \fbox { (5) } \ \)である。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& \left( E-V_{0}\right) \frac {R_{2}}{R_{1}+R_{2}} &(ロ)& E &(ハ)& \frac {t}{C\left( R_{1}+R_{2}\right) } \\[ 5pt ]
&(ニ)& \frac {E}{R_{1}+R_{2}} &(ホ)& C\frac {\mathrm {d}i}{\mathrm {d}t} &(ヘ)& -C\left( R_{1}+R_{2}\right) t \\[ 5pt ]
&(ト)& -\frac {t}{C\left( R_{1}+R_{2}\right) } &(チ)& 0 &(リ)& \frac {1}{C}\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
&(ヌ)& \frac {1}{C}\int i \mathrm {d}t &(ル)& E\frac {R_{2}}{R_{1}+R_{2}} &(ヲ)& E-V_{0} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
抵抗とコンデンサを組み合わせた回路の過渡現象に関する問題です。
(2)がクリアできれば完答を目指すことが可能な問題です。微分方程式が解けるかどうかで点数差がつきやすいので,本番では過渡現象を得点源とできるように準備して下さい。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
過渡現象における\( \ RLC \ \)それぞれの電圧は,線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ v_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ v_{\mathrm{L}} \ \),リアクトル\( \ C \ \)の電圧\( \ v_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
v_{\mathrm{R}} &=& Ri \\[ 5pt ]
v_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
v_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,一般解\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチをオンまたはオフした直後の解で,直前の電圧や電流から変化する時の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left( \ln {x}\right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x &=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
\ln {x}&=&-\alpha t +C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となった場合,対数を外すと,
\[
\begin{eqnarray}
x&=&A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ヌ
回路方程式は,ワンポイント解説「1.過渡現象における\( \ RLC \ \)それぞれの電圧」の通り,
\[
\begin{eqnarray}
R_{1}i+ \frac {1}{C}\int i \mathrm {d}t +R_{2}i&=&E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:イ
(1)解答式の両辺を\( \ t \ \)で微分すると,
\[
\begin{eqnarray}
R_{1}\frac {\mathrm {d}i}{\mathrm {d}t}+ \frac {1}{C}i +R_{2}\frac {\mathrm {d}i}{\mathrm {d}t}&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となるので,変数分離して一般解\( \ i \ \)を求めれば,
\[
\begin{eqnarray}
\left( R_{1}+R_{2}\right) \frac {\mathrm {d}i}{\mathrm {d}t}+ \frac {1}{C}i &=&0 \\[ 5pt ]
\left( R_{1}+R_{2}\right) \frac {\mathrm {d}i}{\mathrm {d}t}&=&-\frac {1}{C}i \\[ 5pt ]
\frac {1}{i}\mathrm {d}i&=&-\frac {1}{C\left( R_{1}+R_{2}\right) }\mathrm {d}t \\[ 5pt ]
\ln i&=&-\frac {1}{C\left( R_{1}+R_{2}\right) }t+C \left( Cは積分定数\right) \\[ 5pt ]
i&=&Ae^{-\frac {1}{C\left( R_{1}+R_{2}\right) }t} \left( Aは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。初期条件\( \ \displaystyle i(0)=\frac {E-V_{0}}{R_{1}+R_{2}} \ \)より,
\[
\begin{eqnarray}
\frac {E-V_{0}}{R_{1}+R_{2}}&=&Ae^{-\frac {1}{C\left( R_{1}+R_{2}\right) }\times 0} \\[ 5pt ]
A&=&\frac {E-V_{0}}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
i&=&\frac {E-V_{0}}{R_{1}+R_{2}} e^{-\frac {1}{C\left( R_{1}+R_{2}\right) }t} \\[ 5pt ]
\end{eqnarray}
\]
となり,抵抗\( \ R_{2} \ \)の電圧\( \ v \ \)は,
\[
\begin{eqnarray}
v&=&R_{2}i \\[ 5pt ]
&=&\left( E-V_{0}\right) \frac {R_{2}}{R_{1}+R_{2}} e^{-\frac {1}{C\left( R_{1}+R_{2}\right) }t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
[別解]
\( \ \displaystyle i=\frac {\mathrm {d}q}{\mathrm {d}t} \ \)より,(1)解答式を変形すると,
\[
\begin{eqnarray}
R_{1}\frac {\mathrm {d}q}{\mathrm {d}t}+ \frac {q}{C} +R_{2}\frac {\mathrm {d}q}{\mathrm {d}t}&=&E \\[ 5pt ]
\left( R_{1}+R_{2}\right) \frac {\mathrm {d}q}{\mathrm {d}t}+ \frac {q}{C} &=&E \\[ 5pt ]
\end{eqnarray}
\]
となる。過渡解を\( \ q_{t} \ \)とすると,
\[
\begin{eqnarray}
\left( R_{1}+R_{2}\right) \frac {\mathrm {d}q_{t}}{\mathrm {d}t}+ \frac {q_{t}}{C} &=&0 \\[ 5pt ]
\left( R_{1}+R_{2}\right) \frac {\mathrm {d}q_{t}}{\mathrm {d}t} &=& -\frac {q_{t}}{C} \\[ 5pt ]
\frac {1}{q_{t}} \mathrm {d}q_{t} &=& -\frac {1}{C\left( R_{1}+R_{2}\right) }\mathrm {d}t \\[ 5pt ]
\ln q_{t} &=& -\frac {1}{C\left( R_{1}+R_{2}\right) }t+C \left( Cは積分定数\right) \\[ 5pt ]
q_{t} &=& Ae^{-\frac {1}{C\left( R_{1}+R_{2}\right) }t} \left( Aは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,定常解を\( \ q_{s} \ \)とすると,
\[
\begin{eqnarray}
\frac {q_{s}}{C} &=&E \\[ 5pt ]
q_{s}&=&CE \\[ 5pt ]
\end{eqnarray}
\]
となるので,一般解\( \ q \ \)は,
\[
\begin{eqnarray}
q &=&q_{s}+q_{t} \\[ 5pt ]
&=&CE+Ae^{-\frac {1}{C\left( R_{1}+R_{2}\right) }t} \\[ 5pt ]
\end{eqnarray}
\]
となる。初期条件\( \ q(0)=CV_{0} \ \)であるから,
\[
\begin{eqnarray}
CV_{0}&=&CE+Ae^{-\frac {1}{C\left( R_{1}+R_{2}\right) }\times 0} \\[ 5pt ]
CV_{0}-CE&=&A \\[ 5pt ]
A&=&C\left( V_{0}-E\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
q &=&CE+C\left( V_{0}-E\right) e^{-\frac {1}{C\left( R_{1}+R_{2}\right) }t} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ C \ \)の電圧\( \ v_{C} \ \)は,
\[
\begin{eqnarray}
v_{C} &=&\frac {q}{C} \\[ 5pt ]
&=&\frac {1}{C}\times \left\{ CE+C\left( V_{0}-E\right) e^{-\frac {1}{C\left( R_{1}+R_{2}\right) }t} \right\} \\[ 5pt ]
&=&E+\left( V_{0}-E\right) e^{-\frac {1}{C\left( R_{1}+R_{2}\right) }t} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,抵抗\( \ R_{2} \ \)の電圧\( \ v \ \)は,
\[
\begin{eqnarray}
v &=&\frac {R_{2}}{R_{1}+R_{2}}\left( E-v_{C}\right) \\[ 5pt ]
&=&\frac {R_{2}}{R_{1}+R_{2}} \left[ E-\left\{ E+\left( V_{0}-E\right) e^{-\frac {1}{C\left( R_{1}+R_{2}\right) }t}\right\} \right] \\[ 5pt ]
&=&\left( E-V_{0}\right) \frac {R_{2}}{R_{1}+R_{2}} e^{-\frac {1}{C\left( R_{1}+R_{2}\right) }t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ト
(2)解答式より,\( \ \displaystyle -\frac {t}{C\left( R_{1}+R_{2}\right) } \ \)と求められる。
(4)解答:チ
(2)解答式より,定常状態\( \ \left( t→\infty \right) \ \)における\( \ v \ \)は\( \ 0 \ \)と求められる。
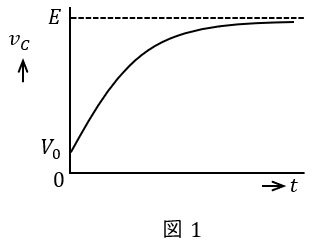
(5)解答:ヨ
(4)より,定常状態において\( \ v_{C}=E-v=E \ \)であるから,初期状態\( \ V_{0} \ \)から徐々に上昇していく。したがって,\( \ v_{C} \ \)の時間的変化は図1のようになる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは