《法規》〈電気施設管理〉[H19:問6]高圧需要家の電力需要設備に関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章，図及び表は，高圧需要家の電力需要設備に関するものである。文中及び表中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる数値を解答群の中から選び，その記号をマークシートに記入しなさい。ただし，\( \ 1 \ \)年間は\( \ 365 \ \)日，負荷\( \ \mathrm {A} \ \)，負荷\( \ \mathrm {B} \ \)及び負荷\( \ \mathrm {C} \ \)の力率はいずれも\( \ 1.0 \ \)とし，変圧器の損失は無視するものとする。

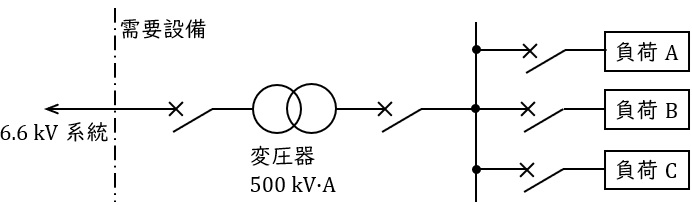
\( \ \mathrm {a.} \ \)電力需要設備は，図のように容量\( \ 500 \ \mathrm {[kV\cdot A]} \ \)の変圧器から，負荷\( \ \mathrm {A} \ \)，負荷\( \ \mathrm {B} \ \)及び負荷\( \ \mathrm {C} \ \)の三つの負荷に電力を供給しており，各負荷の電力使用実績等は表のとおりである。

\[
\begin{array}{|c|c|c|c|}
\hline
& 年間使用電力量 \ \mathrm {[MW\cdot h]} & 最大電力 \ \mathrm {[kW]} & 年負荷率 \ \mathrm {[％]} \\
\hline
負荷 \ \mathrm {A} \ & \ \fbox {　 （１） 　} \ & 167 & 82 \\
\hline
負荷 \ \mathrm {B} \ & 851 & \ \fbox {　 （２） 　} \ & 72 \\
\hline
負荷 \ \mathrm {C} \ & 1 \ 367 & 208 & \ \fbox {　 （３） 　} \ \\
\hline
\end{array}
\] 　　　注：表の値は小数第\( \ 1 \ \)位で四捨五入した値とする。

\( \ \mathrm {b.} \ \)一つの負荷相互間の不等率が\( \ 1.20 \ \)であるとき，合成最大電力は\( \ \fbox {　 （４） 　} \ \mathrm {[kW]} \ \)であり，このときの変圧器の利用率は\( \ \fbox {　 （５） 　} \ \mathrm {[％]} \ \)である。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　70　　　　　&（ロ）&　74　　　　　&（ハ）&　75 \\[ 5pt ] &（ニ）&　79　　　　　&（ホ）&　85　　　　　&（ヘ）&　92 \\[ 5pt ] &（ト）&　97　　　　　&（チ）&　133　　　　　&（リ）&　135 \\[ 5pt ] &（ヌ）&　370　　　　　&（ル）&　393　　　　　&（ヲ）&　425 \\[ 5pt ] &（ワ）&　1 \ 200　　　　　　　&（カ）&　1 \ 463　　　　　　　&（ヨ）&　1 \ 785 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

需要家の需要電力と不等率，負荷率の関係を問う問題です。
\( \ 3 \ \)種の頃からよく出題されているような内容で，\( \ 2 \ \)種では二次試験でも出題される可能性がある内容です。
ヒントがないので，定義式を覚えていないと大きな得点ロスとなってしまいます。需要率，不等率，負荷率の定義式は本番前に必ず見直すようにしましょう。

1.需要率，不等率，負荷率の定義
①需要率
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

②不等率（常に1以上となる)
\[
\begin{eqnarray}
不等率&=&\frac {各最大需要電力の和}{合成した最大需要電力} \\[ 5pt ] \end{eqnarray}
\]

③負荷率
\[
\begin{eqnarray}
負荷率&=&\frac {平均需要電力}{最大需要電力}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)解答：ワ
負荷\( \ \mathrm {A} \ \)の最大電力が\( \ 167 \ \mathrm {[kW]} \ \)，年負荷率が\( \ 82 \ \mathrm {[％]} \ \)なので，平均電力\( \ P_{\mathrm {aA}} \ \mathrm {[kW]} \ \)は，ワンポイント解説「1.需要率，不等率，負荷率の定義」の通り，
\[
\begin{eqnarray}
82&=&\frac {P_{\mathrm {aA}}}{167}\times 100 \\[ 5pt ] P_{\mathrm {aA}}&=&\frac {82\times 167}{100} \\[ 5pt ] &=&136.94 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となるから，年間使用電力量\( \ W_{\mathrm {A}} \ \mathrm {[MW\cdot h]} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {A}}&=&P_{\mathrm {aA}}\times 24 \times 365 \\[ 5pt ] &=&136.94\times 24 \times 365 \\[ 5pt ] &≒&1 \ 199 \ 600 \ \mathrm {[kW\cdot h]}　→　1 \ 200 \ \mathrm {[MW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：リ
負荷\( \ \mathrm {B} \ \)の年間使用電力量が\( \ 851 \ \mathrm {[MW\cdot h]} \ \)なので，平均電力\( \ P_{\mathrm {aB}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {aB}}&=&\frac {851\times 10^{3}}{365\times 24} \\[ 5pt ] &≒&97.146 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となり，年負荷率が\( \ 72 \ \mathrm {[％]} \ \)なので，最大電力\( \ P_{\mathrm {mB}} \ \mathrm {[kW]} \ \)は，ワンポイント解説「1.需要率，不等率，負荷率の定義」の通り，
\[
\begin{eqnarray}
72&=&\frac {P_{\mathrm {aB}}}{P_{\mathrm {mB}}}\times 100 \\[ 5pt ] 72&=&\frac {97.146}{P_{\mathrm {mB}}}\times 100 \\[ 5pt ] P_{\mathrm {mB}}&=&\frac {97.146}{72}\times 100 \\[ 5pt ] &≒&134.93　→　135 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ハ
負荷\( \ \mathrm {C} \ \)の年間使用電力量が\( \ 1 \ 367 \ \mathrm {[MW\cdot h]} \ \)なので，平均電力\( \ P_{\mathrm {aC}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {aC}}&=&\frac {1 \ 367\times 10^{3}}{365\times 24} \\[ 5pt ] &≒&156.05 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] であり，最大電力が\( \ 208 \ \mathrm {[kW]} \ \)なので，年負荷率は，ワンポイント解説「1.需要率，不等率，負荷率の定義」の通り，
\[
\begin{eqnarray}
{年負荷率}_{\mathrm {C}}&=&\frac {P_{\mathrm {aC}}}{208}\times 100 \\[ 5pt ] &=&\frac {156.05}{208}\times 100 \\[ 5pt ] &=&75.024　→　75 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヲ
不等率が\( \ 1.20 \ \)なので，合成最大需要電力\( \ P_{\mathrm {m}} \ \mathrm {[kW]} \ \)は，ワンポイント解説「1.需要率，不等率，負荷率の定義」の通り，
\[
\begin{eqnarray}
P_{\mathrm {m}}&=&\frac {P_{\mathrm {mA}}+P_{\mathrm {mB}}+P_{\mathrm {mC}}}{1.20} \\[ 5pt ] &=&\frac {167+135+208}{1.20} \\[ 5pt ] &=&425 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
変圧器の容量が\( \ 500 \ \mathrm {[kV\cdot A]} \ \)，負荷の力率が\( \ 1 \ \)なので，変圧器の利用率\( \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
利用率&=&\frac {P_{\mathrm {m}}}{500}\times 100 \\[ 5pt ] &=&\frac {425}{500}\times 100 \\[ 5pt ] &=&85 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。