《電力・管理》〈火力〉[H19:問1]故障点に流入する三相短絡電流に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

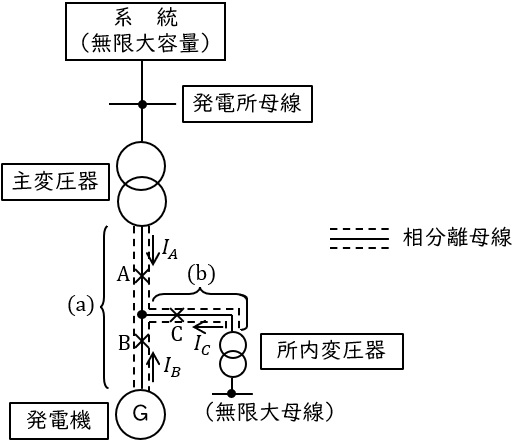
図は，火力発電所の主回路を示したものである。図中\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)，\( \ \mathrm {C} \ \)の各点で三相完全短絡がそれぞれ単独で発生した直後に，図に示す各故障点へ流入する対称短絡電流実効値\( \ I_{A} \ \mathrm {[kA]} \ \)，\( \ I_{B} \ \mathrm {[kA]} \ \)及び\( \ I_{C} \ \mathrm {[kA]} \ \)を算出せよ。次に，これらの電流値をもとに，主回路用相分離母線\( \ \mathrm {(a)} \ \)と所内回路用相分離母線\( \ \mathrm {(b)} \ \)が，短絡電磁力に耐えるために必要な機械的強度設計のベースとなる短絡電流強度（非対称短絡電流実効値）\( \ \mathrm {[kA]} \ \)を求めよ。

なお，計算に際し，系統は無限大容量とする。また，所内変圧器二次側には所内母線があり，短絡事故直後には補機電動機から故障点に短絡電流が供給されるが，簡単のために所内母線は無限大母線として計算せよ。

非対称係数（非対称係数＝非対称短絡電流実効値／対称短絡電流実効値）は\( \ 1.6 \ \)とし，各機器の定数は，次のとおりとする。

〇発電機：\( \ 500 \ \mathrm {[MV\cdot A]} \ \)，\( \ 20 \ \mathrm {[kV]} \ \)，初期過渡リアクタンス\( \ X_{d}^{\prime \prime }=15 \ \mathrm {[％]} \ \)
〇主変圧器：\( \ 480 \ \mathrm {[MV\cdot A]} \ \)，\( \ 20 \ \mathrm {[kV]} / 154 \ \mathrm {[kV]} \ \)，％リアクタンス\( \ Z=12 \ \mathrm {[％]} \ \)
〇所内変圧器：\( \ 70 \ \mathrm {[MV\cdot A]} \ \)，\( \ 20 \ \mathrm {[kV]} / 6.9 \ \mathrm {[kV]} \ \)，％リアクタンス\( \ Z=11 \ \mathrm {[％]} \ \)

【ワンポイント解説】

相分離母線の短絡電流強度設計に関する問題です。
例年問1では火力発電所の論述問題や水力発電の計算問題が出題されやすいですが，本問はかなり特殊な出題形式の問題でした。
今後，類題の再出題の可能性は低いと考えられますが，知識としては送配電分野でも役立つ内容も多いので，理解しておくことをお勧めします。

1.オーム法から百分率インピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると，\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス（パーセントインピーダンス）\( \ ％Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.百分率インピーダンスの容量換算
「1.オーム法からパーセントインピーダンス法への変換」の通り，百分率インピーダンスは基準容量に比例します。したがって，基準容量\( \ P_{\mathrm {A}} \ \mathrm {[V\cdot A]} \ \)から\( \ P_{\mathrm {B}} \ \mathrm {[V\cdot A]} \ \)へ変換する場合の百分率インピーダンスは，
\[
\begin{eqnarray}
％Z_{\mathrm {B}}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}％Z_{\mathrm {A}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.百分率インピーダンスの短絡電流計算
百分率インピーダンスを\( \ ％Z \ \mathrm {[％]} \ \)とすると，三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は，基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)を用いて，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{％Z／100} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z} \\[ 5pt ] \end{eqnarray}
\] で求められます。

※百分率インピーダンスの定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが，試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}I_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}}\times I_{\mathrm {n}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}\times 100}\times 100I_{\mathrm {n}} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

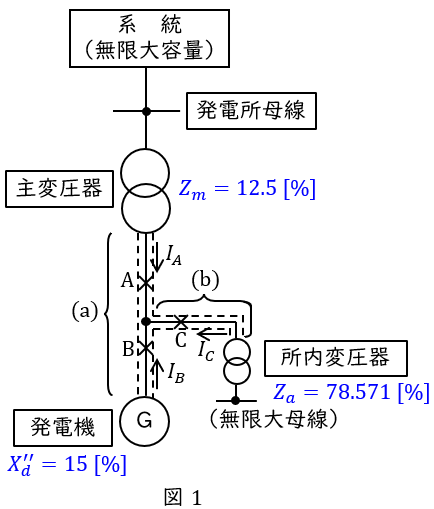
主変圧器，所内変圧器の％インピーダンスを\( \ 500 \ \mathrm {[MV\cdot A]} \ \)換算した％リアクタンス\( \ Z_{m} \ \mathrm {[％]} \ \)及び\( \ Z_{a} \ \mathrm {[％]} \ \)は，ワンポイント解説「2.百分率インピーダンスの容量換算」の通り，
\[
\begin{eqnarray}
Z_{m}&=&\frac {500}{480}\times 12 \\[ 5pt ] &=&12.5 \ \mathrm {[％]} \\[ 5pt ] Z_{a}&=&\frac {500}{70}\times 11 \\[ 5pt ] &≒&78.571 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となる。

よって，故障点からみたインピーダンス\( \ Z_{0} \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
Z_{0}&=&\frac {1}{\displaystyle \frac {1}{X_{d}^{\prime \prime }}+\frac {1}{Z_{m}}+\frac {1}{Z_{a}}} \\[ 5pt ] &=&\frac {1}{\displaystyle \frac {1}{15}+\frac {1}{12.5}+\frac {1}{78.571}} \\[ 5pt ] &≒&\frac {1}{0.159 \ 394} \\[ 5pt ] &≒&6.273 \ 8 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となる。また，基準電流\( \ I_{n} \ \mathrm {[kA]} \ \)は，
\[
\begin{eqnarray}
I_{n}&=&\frac {500\times 10^{6}}{\sqrt {3}\times 20\times 10^{3}} \\[ 5pt ] &≒&14 \ 434 \ \mathrm {[A]}　→　14.434 \ \mathrm {[kA]} \\[ 5pt ] \end{eqnarray}
\] であるから，合成短絡電流\( \ I_{s} \ \mathrm {[kA]} \ \)は，ワンポイント解説「3.百分率インピーダンスの短絡電流計算」の通り，
\[
\begin{eqnarray}
I_{s}&=&\frac {100I_{n}}{Z_{0}} \\[ 5pt ] &=&\frac {100\times 14.434}{6.273 \ 8} \\[ 5pt ] &≒&230.07 \ \mathrm {[kA]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，各故障点へ流入する対称短絡電流実効値\( \ I_{A} \ \mathrm {[kA]} \ \)，\( \ I_{B} \ \mathrm {[kA]} \ \)及び\( \ I_{C} \ \mathrm {[kA]} \ \)は，
\[
\begin{eqnarray}
I_{A}&=&\frac {\displaystyle \frac {1}{Z_{m}}}{\displaystyle \frac {1}{Z_{0}}}I_{s} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{12.5}}{\displaystyle \frac {1}{6.273 \ 8}}\times 230.07 \\[ 5pt ] &=&\frac {6.273 \ 8}{12.5}\times 230.07 \\[ 5pt ] &≒&115.47　→　115 \ \mathrm {[kA]} \\[ 5pt ] I_{B}&=&\frac {\displaystyle \frac {1}{X_{d}^{\prime \prime }}}{\displaystyle \frac {1}{Z_{0}}}I_{s} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{15}}{\displaystyle \frac {1}{6.273 \ 8}}\times 230.07 \\[ 5pt ] &=&\frac {6.273 \ 8}{15}\times 230.07 \\[ 5pt ] &≒&96.228　→　96.3 \ \mathrm {[kA]} \\[ 5pt ] I_{C}&=&\frac {\displaystyle \frac {1}{Z_{a}}}{\displaystyle \frac {1}{Z_{0}}}I_{s} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{78.571}}{\displaystyle \frac {1}{6.273 \ 8}}\times 230.07 \\[ 5pt ] &=&\frac {6.273 \ 8}{78.571}\times 230.07 \\[ 5pt ] &≒&18.371　→　18.4 \ \mathrm {[kA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

\( \ \mathrm {A} \ \)点での事故発生時には主変圧器側から\( \ I_{A}=115.47 \ \mathrm {[kA]} \ \)，発電機及び所内変圧器側から\( \ I_{B}+I_{C} \ \mathrm {[kA]} \ \)が流れ込むので，大小比較すると，
\[
\begin{eqnarray}
I_{B}+I_{C}&=&96.228+18.371≒114.60＜115.47 \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \mathrm {A} \ \)点においては，\( \ 115.47 \ \mathrm {[kA]} \ \)の短絡電流が流れると考えればよい。同様に，\( \ \mathrm {B} \ \)点での事故発生時には発電機側から\( \ I_{B}=96.228 \ \mathrm {[kA]} \ \)，主変圧器及び所内変圧器側から\( \ I_{A}+I_{C} \ \mathrm {[kA]} \ \)が流れ込むので，大小比較すると，
\[
\begin{eqnarray}
I_{A}+I_{C}&=&115.47+18.371≒133.84＞96.228 \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \mathrm {B} \ \)点においては，\( \ 133.84 \ \mathrm {[kA]} \ \)の短絡電流が流れると考えればよく，\( \ \mathrm {C} \ \)点での事故発生時には所内変圧器側から\( \ I_{C}=18.371 \ \mathrm {[kA]} \ \)，主変圧器及び発電機側から\( \ I_{A}+I_{B} \ \mathrm {[kA]} \ \)が流れ込むので，大小比較すると，
\[
\begin{eqnarray}
I_{A}+I_{B}&=&115.47+96.228≒211.70＞18.371 \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \mathrm {C} \ \)点においては，\( \ 211.70 \ \mathrm {[kA]} \ \)の短絡電流が流れると考えればよい。

したがって，主回路用相分離母線\( \ \mathrm {(a)} \ \)については短絡電流の大きい\( \ \mathrm {B} \ \)点での電流値及び所内回路用相分離母線\( \ \mathrm {(b)} \ \)については\( \ \mathrm {C} \ \)点での電流値から考えれば良いので，短絡電磁力に耐えるために必要な機械的強度設計のベースとなる短絡電流強度（非対称短絡電流実効値）\( \ I_{a} \ \mathrm {[kA]} \ \)及び\( \ I_{b} \ \mathrm {[kA]} \ \)は，非対称係数が\( \ 1.6 \ \)であるから，
\[
\begin{eqnarray}
I_{a}&=&1.6\left( I_{A}+I_{C}\right) \\[ 5pt ] &=&1.6\times 133.84 \\[ 5pt ] &≒&214 \ \mathrm {[kA]} \\[ 5pt ] I_{b}&=&1.6\left( I_{A}+I_{B}\right) \\[ 5pt ] &=&1.6\times 211.70 \\[ 5pt ] &≒&339 \ \mathrm {[kA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。