《理論》〈電気回路〉[R07:問6]複数の抵抗とコンデンサを組み合わせた回路の過渡現象に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，複数のコンデンサを持つ電気回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

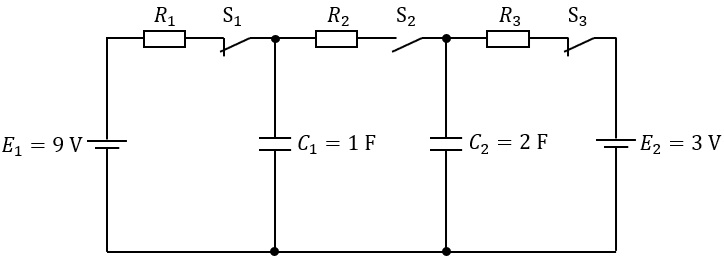
図の回路において，最初スイッチ\( \ \mathrm {S_{1}} \ \)と\( \ \mathrm {S_{3}} \ \)は閉，スイッチ\( \ \mathrm {S_{2}} \ \)は開の状態であり，回路は定常状態にあるとする。\( \ R_{1} \ \)，\( \ R_{2} \ \)，\( \ R_{3} \ \)は抵抗，\( \ E_{1} \ \)，\( \ E_{2} \ \)は直流電圧源である。このとき静電容量\( \ C_{1} \ \)，\( \ C_{2} \ \)のコンデンサの電荷\( \ q_{1} \ \)，\( \ q_{2} \ \)（上側極板が正の場合を正とする）はそれぞれ\( \ \fbox {　 （１） 　} \ \mathrm {C} \ \)及び\( \ \fbox {　 （２） 　} \ \mathrm {C} \ \)である。ここで，\( \ \mathrm {S_{1}} \ \)と\( \ \mathrm {S_{3}} \ \)を開き，次いで時刻\( \ t=0 \ \)で\( \ \mathrm {S_{2}} \ \)を閉じた後のコンデンサ電圧の定常値（両者共通）を求めたい。

\( \ t＞0 \ \)において\( \ q_{1} \ \)と\( \ q_{2} \ \)の和は一定に保たれるので，次の関係がある。
\[
\begin{eqnarray}
\ \fbox {　 （３） 　} \ \ ·················································　① \\[ 5pt ] \end{eqnarray}
\] また，回路中央部の\( \ C_{1} \ \)，\( \ C_{2} \ \)，\( \ R_{2} \ \)からなる閉路で成り立つ閉路方程式は
\[
\begin{eqnarray}
\frac {q_{1}}{C_{1}}&=&\frac {q_{2}}{C_{2}}+R_{2}\frac {\mathrm {d}q_{2}}{\mathrm {d}t} ·······································　② \\[ 5pt ] \end{eqnarray}
\] となる。

②式に①式を代入，整理して\( \ q_{2} \ \)に関する方程式の形で表せば，\( \ \fbox {　 （４） 　} \ \)となる。これを解いて\( \ t \ \)を無限大とすることで\( \ q_{2} \ \)の定常値を知ることができる。これと\( \ C_{2} \ \)からコンデンサ電圧の定常値は\( \ \fbox {　 （５） 　} \ \mathrm {V} \ \)と分かる。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　1　　　　　&（ロ）&　2　　　　　&（ハ）&　3 \\[ 5pt ] &（ニ）&　4　　　　　&（ホ）&　5　　　　　&（ヘ）&　6 \\[ 5pt ] &（ト）&　7　　　　　&（チ）&　8　　　　　&（リ）&　9 \\[ 5pt ] &（ヌ）&　\frac {\mathrm {d}q_{1}}{\mathrm {d}t}=\frac {\mathrm {d}q_{2}}{\mathrm {d}t}　　　　　&（ル）&　q_{1}+q_{2}=C_{1}E_{1}+C_{2}E_{2} 　　　　&（ヲ）&　R_{2}\frac {\mathrm {d}q_{2}}{\mathrm {d}t}+\frac {q_{2}}{C_{2}}=0 \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&（ワ）&　\frac {q_{1}}{C_{1}}+\frac {q_{2}}{C_{2}}=0　　　 \ \ &（カ）&　R_{2}\frac {\mathrm {d}q_{2}}{\mathrm {d}t}+\frac {q_{2}}{C_{1}+C_{2}}=\frac {C_{1}E_{1}+C_{2}E_{2}}{C_{1}} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&（ヨ）&　R_{2}\frac {\mathrm {d}q_{2}}{\mathrm {d}t}+\left( \frac {1}{C_{1}}+\frac {1}{C_{2}}\right) q_{2}=\frac {C_{1}E_{1}+C_{2}E_{2}}{C_{1}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

抵抗とコンデンサを組み合わせた回路の過渡現象に関する問題です。
微分方程式を用いず，計算量もさほど多くないため，例年の過渡現象の問題と比較すると解きやすい問題かと思います。
令和\( \ 7 \ \)年度試験の理論科目は難易度が高めの問題も多かったため，本問はできれば\( \ 4 \ \)つ以上正答しておきたい問題となります。

1.過渡現象におけるリアクトルの過渡状態と定常状態
① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって，リアクトルに電圧を印加した瞬間はほとんど電流は流れないので，開放として考えます。

② 定常状態
電圧を印加して十分時間が経過した後は，リアクトルの抵抗はほぼ零になります。したがって，短絡として考えます。

2.過渡現象におけるコンデンサの過渡状態と定常状態
① 過渡状態
コンデンサに蓄えられている電荷が零であるので，コンデンサに電圧を印加した瞬間は電流がものすごく流れやすい状態，すなわち短絡として考えます。

② 定常状態
コンデンサに電圧を印加しし，十分に時間が経過するとコンデンサに電荷が蓄えられているので，電流をこれ以上蓄えようとしない，すなわち開放として考えます。

【解答】

(1)解答：リ
定常状態\( \ \left( t=0 \right) \ \)において，静電容量\( \ C_{1}=1 \ \mathrm {[F]} \ \)のコンデンサに蓄えられる電荷\( \ q_{1} \ \mathrm {[C]} \ \)は，
\[
\begin{eqnarray}
q_{1}&=&C_{1}E_{1} \\[ 5pt ] &=&1\times 9 \\[ 5pt ] &=&9 \ \mathrm {[C]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヘ
定常状態\( \ \left( t=0 \right) \ \)において，静電容量\( \ C_{2}=2 \ \mathrm {[F]} \ \)のコンデンサに蓄えられる電荷\( \ q_{2} \ \mathrm {[C]} \ \)は，
\[
\begin{eqnarray}
q_{2}&=&C_{2}E_{2} \\[ 5pt ] &=&2\times 3 \\[ 5pt ] &=&6 \ \mathrm {[C]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ル
(1)及び(2)解答式より，\( \ t=0 \ \)において両コンデンサに蓄えられる合計電荷は\( \ C_{1}E_{1}+C_{2}E_{2} \ \mathrm {[C]} \ \)であり，\( \ \mathrm {S_{1}} \ \)と\( \ \mathrm {S_{3}} \ \)を開き，\( \ \mathrm {S_{2}} \ \)を閉じた後の合計電荷は変わらないので，
\[
\begin{eqnarray}
q_{1}+q_{2}&=&C_{1}E_{1}+C_{2}E_{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヨ
(3)解答式より，
\[
\begin{eqnarray}
q_{1}&=&C_{1}E_{1}+C_{2}E_{2}-q_{2} \\[ 5pt ] \end{eqnarray}
\] となるので，これを②式に代入して整理すると，
\[
\begin{eqnarray}
\frac {C_{1}E_{1}+C_{2}E_{2}-q_{2}}{C_{1}}&=&\frac {q_{2}}{C_{2}}+R_{2}\frac {\mathrm {d}q_{2}}{\mathrm {d}t} \\[ 5pt ] \frac {C_{1}E_{1}+C_{2}E_{2}}{C_{1}}-\frac {q_{2}}{C_{1}}&=&\frac {q_{2}}{C_{2}}+R_{2}\frac {\mathrm {d}q_{2}}{\mathrm {d}t} \\[ 5pt ] R_{2}\frac {\mathrm {d}q_{2}}{\mathrm {d}t}+\frac {q_{2}}{C_{1}}+\frac {q_{2}}{C_{2}}&=&\frac {C_{1}E_{1}+C_{2}E_{2}}{C_{1}} \\[ 5pt ] R_{2}\frac {\mathrm {d}q_{2}}{\mathrm {d}t}+\left( \frac {1}{C_{1}}+\frac {1}{C_{2}}\right) q_{2}&=&\frac {C_{1}E_{1}+C_{2}E_{2}}{C_{1}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
(4)解答式において，定常状態では\( \ \displaystyle \frac {\mathrm {d}q_{2}}{\mathrm {d}t}=0 \ \)であるため，これと各値を代入すると，
\[
\begin{eqnarray}
R_{2}\frac {\mathrm {d}q_{2}}{\mathrm {d}t}+\left( \frac {1}{C_{1}}+\frac {1}{C_{2}}\right) q_{2}&=&\frac {C_{1}E_{1}+C_{2}E_{2}}{C_{1}} \\[ 5pt ] R_{2}\times 0+\left( \frac {1}{1}+\frac {1}{2}\right) q_{2}&=&\frac {1\times 9+2\times 3}{1} \\[ 5pt ] \frac {3}{2}q_{2}&=&15 \\[ 5pt ] q_{2}&=&10 \ \mathrm {[C]} \\[ 5pt ] \end{eqnarray}
\] となるので，コンデンサ電圧の定常値\( \ V \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V&=&\frac {q_{2}}{C_{2}} \\[ 5pt ] &=&\frac {10}{2} \\[ 5pt ] &=&5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。