《理論》〈電気回路〉[H23:問5]電流源と抵抗からなる直流回路の電圧に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，電流源と抵抗とからなる直流回路の電圧に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまるものを解答群の中から選びなさい。

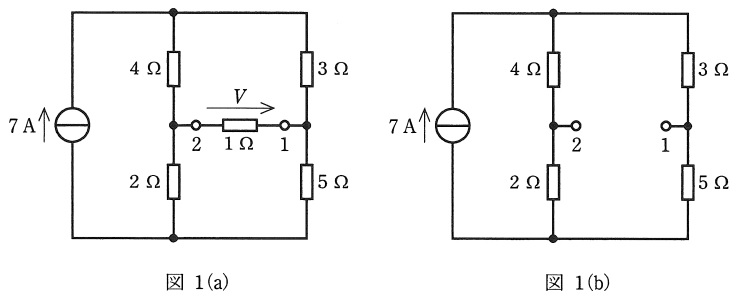
図1(a)の回路において，端子$ \ 1 \ – \ 2 \ $間に現れる電圧$ \ V \ $（端子$ \ 2 \ $を基準にした端子$ \ 1 \ $の電圧）をノートンの定理を使って求めたい。

まず，図1(b)の回路において，端子$ \ 1 \ $，$ \ 2 \ $を短絡したときに端子$ \ 1 \ $から端子$ \ 2 \ $に向かって流れる電流$ \ I \ $は，各抵抗に流れる電流から求めることができる。例えば，$ \ 3 \ \mathrm {[\Omega ]} \ $の抵抗に下向きに流れる電流は$ \ \fbox {　（１）　} \ \mathrm {[A]} \ $であり，その他の抵抗に流れる電流をそれぞれ求めることにより，$ \ I= \ \fbox {　（２）　} \ \mathrm {[A]} \ $となる。次に電流源の大きさを零として，端子$ \ 1 \ $，$ \ 2 \ $よりみたコンダクタンス$ \ g_{\mathrm {i}} \ $を求める。電流源の大きさを零にするということは電流源を$ \ \fbox {　（３）　} \ $することを意味している点に注意すると，$ \ g_{\mathrm {i}}= \ \fbox {　（４）　} \ \mathrm {[S]} \ $となる。以上より，ノートンの定理により$ \ V= \ \fbox {　（５）　} \ \mathrm {[V]} \ $となる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {2}{7}　　　　　　　&（ロ）&　1　　　　　&（ハ）&　そのまま保持 \\[ 5pt ] &（ニ）&　2　　　　&（ホ）&　3　　　　&（ヘ）&　\frac {7}{3} \\[ 5pt ] &（ト）&　\frac {14}{9}　　　　&（チ）&　短絡除去　　　　　　　&（リ）&　\frac {15}{8} \\[ 5pt ] &（ヌ）&　5　　　　&（ル）&　開放除去　　　　&（ヲ）&　\frac {77}{24} \\[ 5pt ] &（ワ）&　4　　　　&（カ）&　\frac {7}{9}　　　　&（ヨ）&　\frac {1}{2} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

ノートンの定理を利用した回路演算に関する問題です。
ノートンの定理自体は受験生でも知らない方も多いかもしれませんが，(1)～(4)はノートンの定理を知らなくても解ける問題，(5)はテブナンの定理を駆使すれば解ける問題となります。
公式や解法を忘れても，自分の持っている知識で点数を加点していくことが重要となります。

1.テブナンの定理
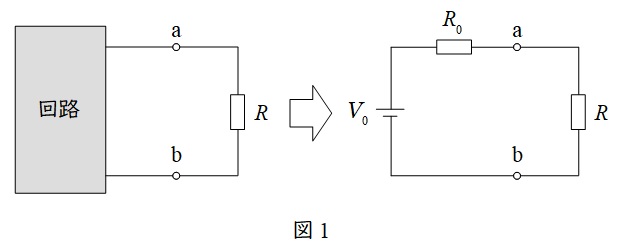
図1のように複雑な回路を電圧源$ \ V_{0} \ $と抵抗$ \ R_{0} \ $に置き換える方法です。
$ \ V_{0} \ $は端子$ \ \mathrm {a} \ – \ \mathrm {b} \ $の開放電圧，$ \ R_{0} \ $は端子$ \ \mathrm {a} \ – \ \mathrm {b} \ $から電源側回路を見た合成抵抗となります。
ただし，$ \ R_{0} \ $を求める際，電圧源は短絡，電流源は開放します。

2.ノートンの定理
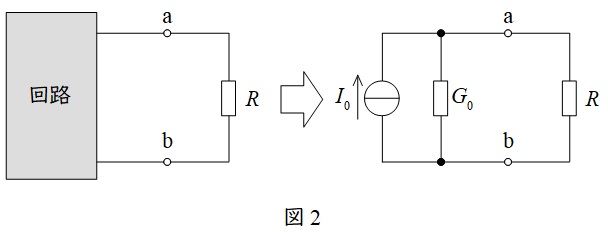
図2のように複雑な回路を電流源$ \ I_{0} \ $とコンダクタンス$ \ G_{0} \ $（抵抗の逆数）に置き換える方法です。
$ \ I_{0} \ $は端子$ \ \mathrm {a} \ – \ \mathrm {b} \ $を短絡したときの短絡電流，$ \ G_{0} \ $は端子$ \ \mathrm {a} \ – \ \mathrm {b} \ $から電源側回路を見た合成コンダクタンスとなります。
ただし，$ \ G_{0} \ $を求める際，電圧源は短絡，電流源は開放します。

【解答】

(1)解答：ワ
図1(b)の回路において，端子$ \ 1 \ $，$ \ 2 \ $を短絡したとき，$ \ 3 \ \mathrm {[\Omega ]} \ $の抵抗に下向きに流れる電流$ \ I_{3} \ \mathrm {[A]} \ $は，分流の法則より，
\[
\begin{eqnarray}
I_{3}&=& \frac {4}{3+4}\times 7 \\[ 5pt ] &=& 4 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ニ
(1)と同様に，端子$ \ 1 \ $，$ \ 2 \ $を短絡したとき，$ \ 4 \ \mathrm {[\Omega ]} \ $，$ \ 2 \ \mathrm {[\Omega ]} \ $，$ \ 5 \ \mathrm {[\Omega ]} \ $の抵抗に下向きに流れる電流$ \ I_{4} \ \mathrm {[A]} \ $，$ \ I_{2} \ \mathrm {[A]} \ $，$ \ I_{5} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I_{4}&=& \frac {3}{3+4}\times 7 \\[ 5pt ] &=& 3 \ \mathrm {[A]} \\[ 5pt ] I_{2}&=& \frac {5}{2+5}\times 7 \\[ 5pt ] &=& 5 \ \mathrm {[A]} \\[ 5pt ] I_{5}&=& \frac {2}{2+5}\times 7 \\[ 5pt ] &=& 2 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，短絡したときに$ \ 1 \ – \ 2 \ $間に流れる電流$ \ I \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I&=&I_{3}-I_{5} \\[ 5pt ] &=&4-2 \\[ 5pt ] &=& 2 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ル
電流源の大きさを零とすることは，電流が流れないようにする，すなわち開放除去することである。

(4)解答：イ
電流源を開放したときに端子$ \ 1 \ – \ 2 \ $から見た合成抵抗$ \ R_{0} \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
R_{0}&=&\frac {\left( 3+4\right) \times \left( 2+5\right) }{\left( 3+4\right) +\left( 2+5\right) } \\[ 5pt ] &=& \frac {7}{2} \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるから，端子$ \ 1 \ – \ 2 \ $から見たコンダクタンス$ \ g_{\mathrm {i}} \ \mathrm {[S]} \ $は，
\[
\begin{eqnarray}
g_{\mathrm {i}}&=&\frac {1}{R_{0}} \\[ 5pt ] &=& \frac {2}{7} \ \mathrm {[S]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

※元の各抵抗の逆数をとって，合成コンダクタンスを求める方法が所謂「模範的な解答」と思いますが，ここでは合成抵抗を求めてから逆数をとる方法の方が速いと考えられるため，こちらを採用しています。

(5)解答：ト
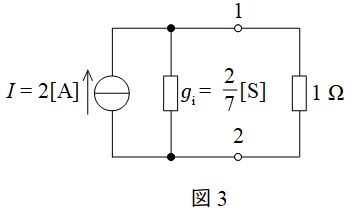
ワンポイント解説「2.ノートンの定理」の通り，(1)～(4)に沿って図1(a)を書き換えると図3のようになる。
図3に分流の法則を適用すると，$ \ 1 \ \mathrm {[\Omega ]} \ $の抵抗に流れる電流$ \ I_{1} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I_{1}&=&\frac {\displaystyle \frac {1}{g_{\mathrm {i}}}}{\displaystyle \frac {1}{g_{\mathrm {i}}}+1}I \\[ 5pt ] &=&\frac {\displaystyle \frac {7}{2}}{\displaystyle \frac {7}{2}+1}\times 2 \\[ 5pt ] &=& \frac {14}{9} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，電圧$ \ V \ \mathrm {[V]} \ $は，
\[
\begin{eqnarray}
V&=&1\times I_{1} \\[ 5pt ] &=&1\times \frac {14}{9} \\[ 5pt ] &=& \frac {14}{9} \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。