【質問】
平成29年度電力管理問5で零相電圧と対地静電容量の関係を記述する問いがあったと思います。
その中で系統が長くなると対地静電容量が大きくなり、充電電流が多くなり零相電圧が小さくなるとありました。
系統が長くなることで対地静電容量と充電電流が大きくなることは理解できるのですがそれに伴って零相電圧が小さくなるのは何故でしょうか。
お忙しいところ大変申し訳ございませんがご回答のほど宜しくお願い致します。
【回答】
お問い合わせありがとうございました。
言葉でお伝えするのは非常に難しいのですが,地絡電流のうち対地静電容量に還流する電流の量があまり変化せず,\(\displaystyle V= \frac {I}{j\omega C}\)の関係があるため,対地静電容量\(C\)が大きくなると各相の電圧が下がるためです。
零相電圧\(\displaystyle V_{0}=\frac {1}{3} ( V_{\mathrm {a}}+V_{\mathrm {b}}+V_{\mathrm {c}})\)の関係がありますので各相の電圧に比例して零相電圧が下がります。
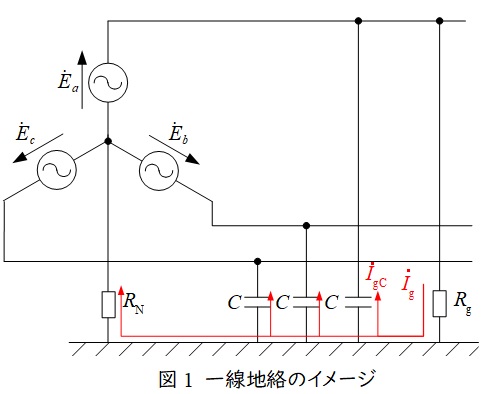
図1のイメージで言いますと,(本来無視できませんが)簡単の為に\(R_{\mathrm {N}}\)と線路の抵抗やリアクタンスを無視すると,対地静電容量を通じて各相へ流れる電流\(\displaystyle I_{\mathrm {gC}}≒\frac {1}{3}I_{\mathrm {g}}\)となるので,各相の電圧\(\displaystyle V_{\mathrm {a}}=V_{\mathrm {b}}=V_{\mathrm {c}}=\frac {I_{\mathrm {gC}}}{j\omega C}=\frac {I_{\mathrm {g}}}{j3\omega C}\)となります。
したがって,零相電圧\(V_{0}\)は対称座標法の定義から,
\[
\begin{eqnarray}
V_{0}&=&\frac {1}{3}\left( V_{\mathrm {a}}+V_{\mathrm {b}}+V_{\mathrm {c}}\right) \\[ 5pt ]
&=&\frac {1}{3}\left( \frac {I_{\mathrm {g}}}{j3\omega C}+\frac {I_{\mathrm {g}}}{j3\omega C}+\frac {I_{\mathrm {g}}}{j3\omega C}\right) \\[ 5pt ]
&=&\frac {I_{\mathrm {g}}}{j3\omega C} \\[ 5pt ]
\end{eqnarray}
\]
となるため,対地静電容量が大きいほど,零相電圧は小さくなることになります。
正確に零相電圧の導出するには対称座標法を用いる必要があります。外部ホームーページになりますが,下記URLの中段のところに対称座標法による零相電圧の導出の式があります。
ご参考になさって頂ければ幸いです。




 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは