《機械》〈パワーエレクトロニクス〉[H30:問3]チョッパ回路に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，チョッパ回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

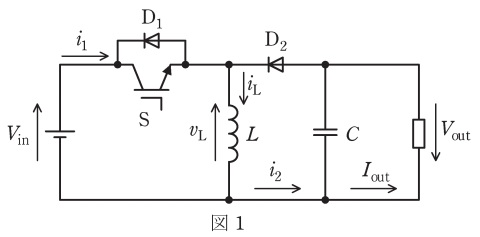
図1は，$ \ \fbox {　（１）　} \ $チョッパの回路図である。平滑コンデンサ$ \ C \ $の静電容量は十分に大きく，出力電圧$ \ V_{\mathrm {out}} \ $及び出力電流$ \ I_{\mathrm {out}} \ $のリプルは無視できるものとする。図2，3は，定常状態におけるインダクタの電圧$ \ v_{\mathrm {L}} \ $及び電流$ \ i_{\mathrm {L}} \ $の波形であり，スイッチ$ \ \mathrm {S} \ $がオンの期間を$ \ T_{\mathrm {on}} \ $，オフの期間を$ \ T_{\mathrm {off}} \ $とする。

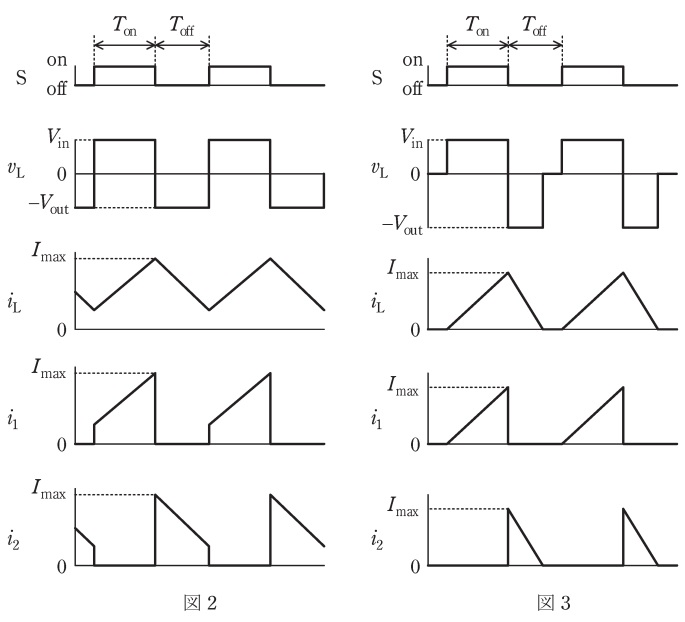
図2は出力電流$ \ I_{\mathrm {out}} \ $が大きく，インダクタ電流$ \ i_{\mathrm {L}} \ $が常に正の場合で，電流連続モードと呼び，このときの出力電圧が，$ \ V_{\mathrm {out}}=\fbox {　（２）　} \ $となることは，よく知られている。ここで，デューティ比$ \ \displaystyle D=\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ $を用いると，$ \ V_{\mathrm {out}}=\fbox {　（３）　}V_{\mathrm {in}} \ $と表すこともできる。

一方，出力電流$ \ I_{\mathrm {out}} \ $を低減すると，図3のようにインダクタ電流$ \ i_{\mathrm {L}} \ $に零となる期間が現れる。図3の場合を電流断続モード(電流不連続モード)と呼ぶ。定常状態では，インダクタ電圧$ \ v_{\mathrm {L}} \ $の1周期の平均値は常に$ \ \fbox {　（４）　} \ $でなければならない。電流連続モードと電流断続モードとでスイッチ$ \ \mathrm {S} \ $のゲート信号が同じであれば，$ \ V_{\mathrm {out}} \ $は$ \ \fbox {　（５）　} \ $なる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　昇降圧　　　&（ロ）&　正　　　&（ハ）&　\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ] &（ニ）&　降圧　　　&（ホ）&　両者で等しく　　　&（ヘ）&　\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ] &（ト）&　負　　　&（チ）&　D　　　&（リ）&　電流断続モードの方が高く \\[ 5pt ] &（ヌ）&　\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}V_{\mathrm {in}} 　　　&（ル）&　1-D　　　&（ヲ）&　\frac {D}{1-D} \\[ 5pt ] &（ワ）&　零　　　&（カ）&　昇圧　　　&（ヨ）&　電流連続モードの方が高く \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

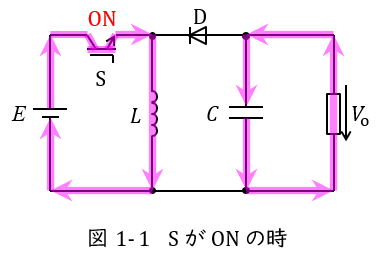
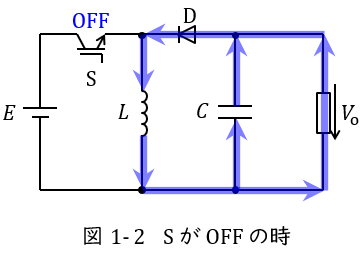
昇圧チョッパや降圧チョッパの内容は電験三種からよく出題されていたと思います。パワーエレクトロニクスの場合はオンの時回路がどうなるか，オフの時回路がどうなるか考えることが肝要です。この問題図の場合は図1-1，1-2のような動作電流の流れとなります。

1.昇降圧チョッパの動作
問題図は昇降圧チョッパの例となります。
スイッチ$ \ \mathrm {S} \ $がオンになると，図1-1のように電源からの電流はスイッチ$ \ \mathrm {S} \ $を通り，リアクトル$ \ L \ $側に電流が流れますが，ダイオードは逆向きなので電流が流れません。また，コンデンサに蓄えられている電荷が出力側に流れます。
スイッチ$ \ \mathrm {S} \ $がオフになると，図1-2のように電源から電流は流れず，リアクトルとコンデンサから出力側に電流が流れます。
昇降圧チョッパは昇圧と降圧の両方ができ，デューティ比$ \ \displaystyle D=\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ $が50％より大きいと昇圧，50％より小さいと降圧となります。また，定常状態では$ \ v_{\mathrm {L}} \ $の平均電圧が零となる必要があります。

【関連する「電気の神髄」記事】

　　昇降圧チョッパ回路の理論

【解答】

(1)解答：イ
題意より，解答候補は（イ）昇降圧，（ニ）降圧，（カ）昇圧，になると思います。問題図の回路は典型的な昇降圧チョッパの回路図です。

(2)解答：ハ
昇降圧チョッパでは，$ \ v_{\mathrm {L}} \ $の平均電圧が零であるから，
\[
\begin{eqnarray}
V_{\mathrm {in}}T_{\mathrm {on}}&=&V_{\mathrm {out}}T_{\mathrm {off}} \\[ 5pt ] \end{eqnarray}
\] が成立しなければならない。よって，上式を$ \ V_{\mathrm {out}} \ $について整理すると，
\[
\begin{eqnarray}
V_{\mathrm {out}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヲ
$ \ \displaystyle D=\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ $を整理すると，
\[
\begin{eqnarray}
T_{\mathrm {on}}&=&D\left( T_{\mathrm {on}}+T_{\mathrm {off}}\right) \\[ 5pt ] \left( 1-D\right) T_{\mathrm {on}}&=&DT_{\mathrm {off}} \\[ 5pt ] T_{\mathrm {on}}&=&\frac {D}{1-D}T_{\mathrm {off}} \\[ 5pt ] \end{eqnarray}
\] となるので，(2)の解答式に代入すると，
\[
\begin{eqnarray}
V_{\mathrm {out}}&=&\frac {\displaystyle T_{\mathrm {on}}}{T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ] &=&\frac {\displaystyle \frac {D}{1-D}T_{\mathrm {off}}}{T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ] &=&\frac {D}{1-D}V_{\mathrm {in}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ワ
ワンポイント解説「1.昇降圧チョッパの動作」の通り，インダクタ電圧$ \ v_{\mathrm {L}} \ $は定常状態において平均電圧が零となる必要があります。

(5)解答：リ
インダクタ電圧$ \ v_{\mathrm {L}} \ $は定常状態において平均電圧が零となり，インダクタ電流$ \ i_{\mathrm {L}} \ $が零となる期間は$ \ v_{\mathrm {L}} \ $は零となるので，図2，図3で描かれている通り，$ \ V_{\mathrm {out}} \ $は電流断続モードの方が高くなります。