《機械》〈パワーエレクトロニクス〉[H29:問3] 電圧形インバータに関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，電圧形インバータに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

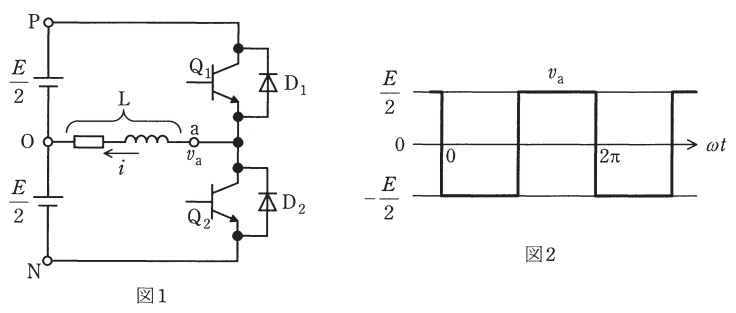
図1には電圧形ハーフブリッジインバータを示す。負荷は誘導性負荷$ \ \mathrm {L} \ $で，今$ \ \mathrm {Q_{1}} \ $がオンして負荷電流が$ \ \mathrm {P-Q_{1}-L-O} \ $の経路で流れているとする。その後のある時刻で，$ \ \mathrm {Q_{1}} \ $をオフして$ \ \mathrm {Q_{2}} \ $にオン信号を与えた。この直後に流れる電流の経路は$ \ \fbox {　（１）　} \ $となる。実際の電圧形インバータでは，$ \ \mathrm {Q_{1}} \ $にオフ信号を与えてから$ \ \mathrm {Q_{2}} \ $にオン信号を与えるまでに所定の時間をとっている。この時間を$ \ \fbox {　（２）　} \ $といい，ターンオフの遅れなどによって短絡電流が流れるのを未然に防止する目的で設けている。電圧形インバータでは，直流電源とインバータからなる回路の$ \ \fbox {　（３）　} \ $してあるので，もし短絡すると大きな短絡電流が流れてしまう。
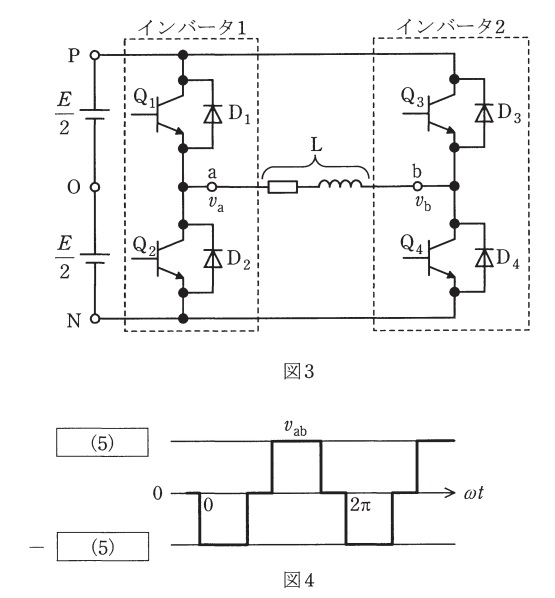
図1のインバータの出力電圧波形を図2に示す。この電圧$ \ v_{\mathrm {a}}$は，直流電源の$ \ \fbox {　（４）　} \ $端子から$ \ \mathrm {a} \ $端子を見たときの電圧である。図1のハーフブリッジインバータを$ \ 2 \ $台使用したのが，図3の電圧形フルブリッジインバータである。このときの出力電圧$ \ v_{\mathrm {ab}} \ $は，$ \ v_{\mathrm {ab}}=v_{\mathrm {a}}-v_{\mathrm {b}} \ $と表せる。インバータ$ \ 1 \ $とインバータ$ \ 2 \ $が位相差$ \ 120° \ $で運転したときの出力電圧波形は図4となり，この電圧$ \ v_{\mathrm {ab}} \ $の波高値は$ \ \fbox {　（５）　} \ $となる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　\mathrm {O-L-Q_{2}-N}　　　　　&（ロ）&　プラス母線 \ \mathrm {P}　　　　　&（ハ）&　キャパシタンスを小さく \\[ 5pt ] &（ニ）&　デッドタイム　　　　　&（ホ）&　\mathrm {O-L-D_{1}-P}　　　　　&（ヘ）&　インダクタンスを小さく \\[ 5pt ] &（ト）&　マイナス母線 \ \mathrm {N}　　　　　&（チ）&　\frac {E}{2}　　　　　&（リ）&　\mathrm {N-D_{2}-L-O} \\[ 5pt ] &（ヌ）&　電流零期間　　　　　&（ル）&　ターンオフタイム　　　　　&（ヲ）&　インダクタンスを大きく \\[ 5pt ] &（ワ）&　中間電位点 \ \mathrm {O}　　　　　&（カ）&　E　　　　　&（ヨ）&　\frac {\sqrt {3}}{2}E
\end{eqnarray}
\]

【ワンポイント解説】

電圧形インバータは二次試験でよく出題される内容です。電圧形インバータと電流形インバータの比較は頻出なので，本問とは関係なくよく理解しておく必要があります。

1.電圧形インバータと電流形インバータ
\[
\begin{array}{|c|c|c|}
\hline
& 電圧形インバータ & 電流形インバータ \\
\hline
動作 & 電圧源 & 電流源 \\
\hline
電圧波形 & 方形波 & 正弦波 \\
\hline
電流波形 & ほぼ正弦波 & 方形波 \\
\hline
\end{array}
\]

【関連する「電気の神髄」記事】

　　単相電圧形ハーフブリッジインバータ
　　単相電圧形フルブリッジインバータ

【解答】

(1)解答：リ
題意より，解答候補は$（イ）\mathrm {O-L-Q_{2}-N}$，$（ホ）\mathrm {O-L-D_{1}-P}$，$（リ）\mathrm {N-D_{2}-L-O}$，となります。逆の電圧がかかるため，電流の向きが逆になりそうですが，$ \ \mathrm {L} \ $にリアクトルがあるため，切替え直後に$ \ \mathrm {L} \ $に流れる電流は，切替え前と同方向になります。よって解答は$（リ）\mathrm {N-D_{2}-L-O}$となります。

(2)解答：ニ
題意より，解答候補は（ニ）デッドタイム，（ヌ）電流零期間，（ル）ターンオフタイム，となります。リアクトルがある以上，電流零となる期間ほとんどありません。また，ターンオフタイムはオン状態からオフ状態になる間の時間となります。よって解答は（ニ）デッドタイムとなります。

(3)解答：ヘ
題意より，解答候補は（ハ）キャパシタンスを小さく，（ヘ）インダクタンスを小さく，（ヲ）インダクタンスを大きく，となります。電圧形インバータでは，出力波形を方形波に近づけるため，直流電源とインバータの回路のインダクタンスを小さくしています。そのため，短絡すると大きな過電流が流れます。解答の選択肢のうち，（ハ）キャパシタンスを小さくと（ヲ）インダクタンスを大きくでは短絡電流が小さくなります。

(4)解答：ワ
題意より，解答候補は（ロ）プラス母線$ \ \mathrm {P} \ $，（ト）マイナス母線$ \ \mathrm {N} \ $，（ワ）中間電位点$ \ \mathrm {O} \ $，となります。出力波形の波高値は$ \ \displaystyle \frac{E}{2} \ $であり，該当するのは$ \ \mathrm {O} \ $端子のみになります。

(5)解答：カ
題意より，解答候補は$ \ \displaystyle （チ）\frac {E}{2} \ $，$ \ （カ）E \ $，$ \ \displaystyle （ヨ）\frac {\sqrt {3}}{2}E \ $，となります。
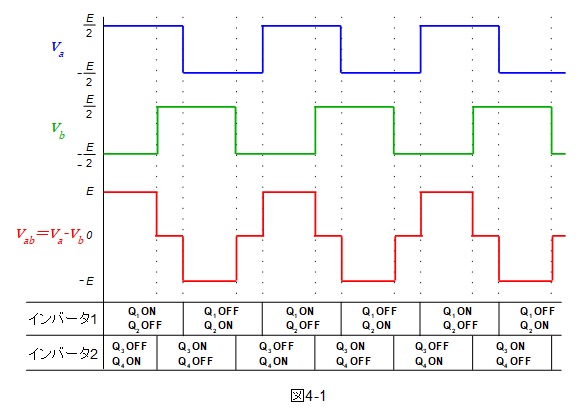
題意の通り，インバータ$ \ 1 \ $とインバータ$ \ 2 \ $を位相差$ \ 120° \ $で運転した時の出力は図4-1の通りとなります。したがって，解答は$ \ （カ）E \ $となります。