Contents
【問題】
【難易度】★★★☆☆(普通)
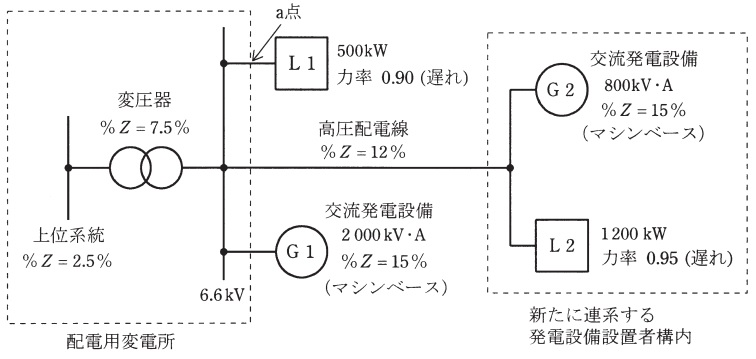
図のように,\( \ 2 \ 000 \ \mathrm {[kV\cdot A]} \ \)の発電設備が連系されている配電用変電所において,新たに\( \ 800 \ \mathrm {[kV\cdot A]} \ \)の発電設備を連系する際の\( \ \ \mathrm {a} \ \)点における三相短絡電流計算について,次の問に答えよ。
なお,各地点の\( \ %Z \ \)は図中に示したとおりの値であり,特に断りのない場合は,\( \ 10 \ \mathrm {[MV\cdot A]} \ \)ベースである。また,線路の抵抗は無視できるものとし,配電用変電所から\( \ \mathrm {L1} \ \)及び\( \ \mathrm {G1} \ \)までの高圧配電線はこう長が短いことから\( \ %Z \ \)は無視できるものとする。
(1) 連系する\( \ 800 \ \mathrm {[kV\cdot A]} \ \)の発電設備の\( \ %Z \ \)(\( \ 10 \ \mathrm {[MV\cdot A]} \ \)ベース)を求めよ。
(2) \( \ 800 \ \mathrm {[kV\cdot A]} \ \)の発電設備を連系した後における\( \ \ \mathrm {a} \ \)点の三相短絡インピーダンス\( \ %Z \ \)(\( \ 10 \ \mathrm {[MV\cdot A]} \ \)ベース)を求めよ。
(3) \( \ 800 \ \mathrm {[kV\cdot A]} \ \)の発電設備を連系した後における\( \ \ \mathrm {a} \ \)点の三相短絡電流値\( \ \mathrm {[kA]} \ \)を求めよ。
(4) (3)において,\( \ \ \mathrm {a} \ \)点の三相短絡電流値\( \ \mathrm {[kA]} \ \)を遮断器の定格遮断電流(\( \ 10 \ \mathrm {[kA]} \ \))以下に抑制するために,新たに連系する発電設備設置者構内に限流リアクトルを設置する場合におけるリアクトルの最低インピーダンス\( \ %Z \ \)(\( \ 10 \ \mathrm {[MV\cdot A]} \ \)ベース)を求めよ。
【ワンポイント解説】
百分率インピーダンスの導出から三相短絡電流の導出をする計算問題です。
非常によくあるパターンの百分率インピーダンスを用いた計算なので,勉強が進んでいる受験生であれば完答できる方もいると思いますが,(4)は計算に時間がかかるので試験本番においては敢えて後回しにする方法等も検討する必要があります。
百分率インピーダンスに慣れるまでは,少し壁を感じるかもしれませんが,慣れてしまえばオーム法の計算と変わらずに計算ができるようになります。
1.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \),基準電流を\( \ I_{\mathrm {n}} \ \)とすると,
\[
\begin{eqnarray}
%Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.百分率インピーダンス容量換算
「1.オーム法からパーセントインピーダンス法への変換」の通り,百分率インピーダンスは基準容量に比例します。したがって,基準容量\( \ P_{\mathrm {A}} \ \)から\( \ P_{\mathrm {B}} \ \)へ変換する場合の百分率インピーダンスは,
\[
\begin{eqnarray}
%Z_{\mathrm {B}}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}%Z_{\mathrm {A}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.百分率インピーダンスの短絡電流計算
百分率インピーダンスを\( \ %Z \ \)とすると,三相短絡電流\( \ I_{\mathrm {s}} \ \)は,基準電流\( \ I_{\mathrm {n}} \ \)を用いて,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{%Z/100} \\[ 5pt ]
&=&\frac {100I_{\mathrm {n}}}{%Z} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
※百分率インピーダンスの定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}}} \ \)から上式を求めることはできますが,試験時には暗記しておいた方が良いと思います。
【解答】
(1)連系する\( \ 800 \ \mathrm {[kV\cdot A]} \ \)の発電設備の\( \ %Z \ \)(\( \ 10 \ \mathrm {[MV\cdot A]} \ \)ベース)
連系する交流発電設備\( \ \mathrm {G2} \ \)は\( \ %Z_{\mathrm {G2}}=15 \ \mathrm {[%]} \ \)(\( \ 800 \ \mathrm {[kV\cdot A]} \ \)ベース)であるから,ワンポイント解説「2.百分率インピーダンス容量換算」により\( \ 10 \ \mathrm {[MV\cdot A]} \ \)ベースに容量換算すると,
\[
\begin{eqnarray}
%Z_{\mathrm {G2}}^{\prime }&=&\frac {10\times 10^{6}}{800\times 10^{3}}%Z_{\mathrm {G2}} \\[ 5pt ]
&=&\frac {10\times 10^{6}}{800\times 10^{3}}\times 15 \\[ 5pt ]
&=&187.5 → 188 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ 800 \ \mathrm {[kV\cdot A]} \ \)の発電設備を連系した後における\( \ \ \mathrm {a} \ \)点の三相短絡インピーダンス\( \ %Z \ \)(\( \ 10 \ \mathrm {[kV\cdot A]} \ \)ベース)
交流発電設備\( \ \mathrm {G1} \ \)の\( \ %Z_{\mathrm {G1}}=15 \ \mathrm {[%]} \ \)(\( \ 2000 \ \mathrm {[kV\cdot A]} \ \)ベース)を\( \ 10 \ \mathrm {[MV\cdot A]} \ \)ベースに容量換算すると,
\[
\begin{eqnarray}
%Z_{\mathrm {G1}}^{\prime }&=&\frac {10\times 10^{6}}{2000\times 10^{3}}%Z_{\mathrm {G1}} \\[ 5pt ]
&=&\frac {10\times 10^{6}}{2000\times 10^{3}}\times 15 \\[ 5pt ]
&=&75 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
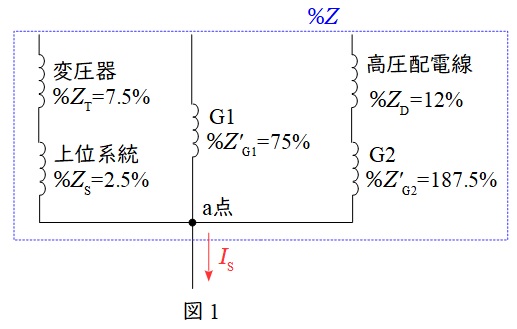
となる。三相短絡事故時には,上位系統,交流発電設備\( \ \mathrm {G1} \ \),交流発電設備\( \ \mathrm {G2} \ \)から,\( \ \mathrm {a} \ \)点に向かい事故電流が流れるので,三相短絡事故時の\( \ \mathrm {a} \ \)点から見た等価回路は図1のようになる。
図1より,\( \ \mathrm {a} \ \)点の短絡インピーダンス\( \ %Z \ \)(\( \ 10 \ \mathrm {[kV\cdot A]} \ \)ベース)は,
\[
\begin{eqnarray}
%Z&=&\frac {1}{\displaystyle \frac {1}{7.5+2.5}+\frac {1}{75}+\frac {1}{12+187.5}} \\[ 5pt ]
&≒&\frac {1}{0.118346} \\[ 5pt ]
&≒&8.4498 → 8.45 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ 800 \ \mathrm {[kV\cdot A]} \ \)の発電設備を連系した後における\( \ \ \mathrm {a} \ \)点の三相短絡電流値\( \ \mathrm {[kA]} \ \)
\( \ \ \mathrm {a} \ \)点での定格電流\( \ \ I_{\mathrm {n}} \ \)の大きさは,
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ]
&≒&\frac {10\times 10^{6}}{\sqrt {3}\times 6.6\times 10^{3}} \\[ 5pt ]
&≒&874.77 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,ワンポイント解説「3.百分率インピーダンスの短絡電流計算」より,\( \ \ \mathrm {a} \ \)点における三相短絡電流値\( \ I_{\mathrm {S}} \ \mathrm {[kA]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {S}}&=&\frac {100I_{\mathrm {n}}}{%Z} \\[ 5pt ]
&=&\frac {100\times 874.77}{8.4498} \\[ 5pt ]
&≒&10353 \ \mathrm {[A]} → 10.4 \ \mathrm {[kA]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)新たに連系する発電設備設置者構内に設置する限流リアクトルの最低インピーダンス\( \ %Z \ \)(\( \ 10 \ \mathrm {[MV\cdot A]} \ \)ベース)
限流リアクトルを設置した場合の等価回路は図2のようになる。(2),(3)と同様に\( \ \mathrm {a} \ \)点から見た短絡インピーダンス\( \ %Z^{\prime } \ \)(\( \ 10 \ \mathrm {[kV\cdot A]} \ \)ベース)を求める式を導出すると,
\[
\begin{eqnarray}
%Z^{\prime }&=&\frac {1}{\displaystyle \frac {1}{7.5+2.5}+\frac {1}{75}+\frac {1}{12+%Z_{\mathrm {L}}+187.5}} \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
I_{\mathrm {S}}&=&\frac {100I_{\mathrm {n}}}{%Z^{\prime }} \\[ 5pt ]
%Z^{\prime }&=&\frac {100I_{\mathrm {n}}}{I_{\mathrm {S}}} \\[ 5pt ]
&=&\frac {100\times 874.77}{10\times 10^{3}} \\[ 5pt ]
&=&8.7477 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
であるので,
\[
\begin{eqnarray}
8.7477&=&\frac {1}{\displaystyle \frac {1}{7.5+2.5}+\frac {1}{75}+\frac {1}{12+%Z_{\mathrm {L}}+187.5}} \\[ 5pt ]
\frac {1}{10}+\frac {1}{75}+\frac {1}{12+%Z_{\mathrm {L}}+187.5}&=&\frac {1}{8.7477} \\[ 5pt ]
\frac {1}{12+%Z_{\mathrm {L}}+187.5}&=&\frac {1}{8.7477}-\frac {1}{10}-\frac {1}{75} \\[ 5pt ]
&≒&0.00098243 \\[ 5pt ]
12+%Z_{\mathrm {L}}+187.5&≒&1017.9 \\[ 5pt ]
%Z_{\mathrm {L}}&≒&818 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※ 上式の計算途中に非常に小さい値が出てくるので,有効数字や計算方法により多少の誤差が生じます。試験センターにおいても複数の正答ありと説明されています。













 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは