《電力》〈送電〉[H25:問3]電力系統に生じる電力動揺に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，電力系統に生じる電力動揺に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。ただし，発電機の$ \ \mathrm {AVR} \ $の効果は考慮しないものとする。

遠隔地電源から無限大母線へ遅れ力率で送電している超高圧並行$ \ 2 \ $回線送電線において，その片回線が開放され，生じた電力動揺が収まった後に投入された。片回線開放直後，発電端電圧は急に$ \ \fbox {　（１）　} \ $し，その後ある周期で振動する。投入時もやはり発電機電圧は投入に伴って急変した後，ある周期で振動する。通常，開放後の動揺周期と投入後の動揺周期を比べると$ \ \fbox {　（２）　} \ $が，これは以下の理由による。

超高圧架空送電系統では送電線の抵抗，静電容量成分はリアクタンス成分に比べて小さいので，送電電力$ \ P \ $は発電機内部電圧及び無限大母線電圧の大きさ$ \ V_{1} \ $，$ \ V_{2} \ $とそれらの位相差$ \ \delta \ $並びに発電機から送電線にかけてのリアクタンスの総和$ \ X \ $を用いて近似的に$ \ \fbox {　（３）　} \ $と表すことができる。両電圧及びリアクタンスをパラメータとし，$ \ \delta \ $を横軸，$ \ P \ $を縦軸として表した曲線を$ \ P-\delta \ $カーブとも呼んでいる。片回線開放後は$ \ X \ $の値が大きくなるので，定常状態で比較すると，投入時に対して開放後の$ \ \delta \ $の値の方が$ \ \fbox {　（４）　} \ $。

このため，開放後並びに投入時の定常状態における$ \ P-\delta \ $カーブの接線の傾きを比較すると開放後の方が小さい。これは電力動揺によって$ \ \delta \ $が変化しても，それを戻そうとする作用が弱い，すなわち$ \ \fbox {　（５）　} \ $が小さいことを意味し，このため電力動揺周期を開放後と投入後で比べると$ \ \fbox {　（２）　} \ $。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　後者の方が長い　　　　　&（ロ）&　同期化力係数　　　　　&（ハ）&　系統定数 \\[ 5pt ] &（ニ）&　P=\frac {V_{1}\cos \delta -V_{2}}{X}V_{2}　　　&（ホ）&　P=\frac {V_{1}\sin \delta -V_{2}}{X}V_{2}　　　&（ヘ）&　P=\frac {V_{1}V_{2}}{X}\cos \delta \\[ 5pt ] &（ト）&　上　昇　　　　　&（チ）&　P=\frac {V_{1}V_{2}}{X}\sin \delta　　　&（リ）&　小さい \\[ 5pt ] &（ヌ）&　大きい　　　　　&（ル）&　低　下　　　　　&（ヲ）&　消　失 \\[ 5pt ] &（ワ）&　制動力係数　　　　　&（カ）&　慣性定数　　　　　&（ヨ）&　前者の方が長い \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

系統の安定度に関する問題で，一次二次問わず非常に出題されやすい問題と言えます。文章で追うとなかなか難しくなってしまうので，こういう問題の場合は図を描いてどうなるかを考えることが大事であると思います。

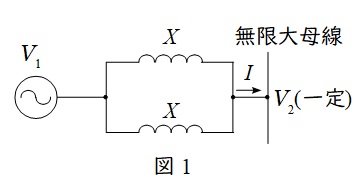
1.並行$ \ 2 \ $回線送電線での開放前後の発電機電圧
本問の場合は並行$ \ 2 \ $回線送電線で開放前後の発電電圧がどうなるかという問題なので，一定である無限大母線電圧を基準に考えると図1のようなイメージとなります。
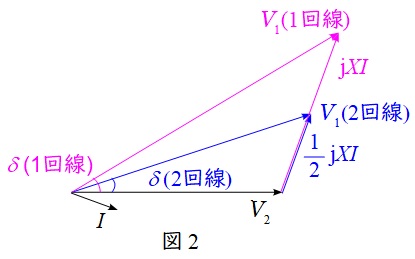
図1において，片回線開放前後でリアクタンスが$ \ \displaystyle \frac {1}{2}\mathrm {j}X \ $→$ \ \displaystyle \mathrm {j}X \ $と変わるので，図2のようなベクトル図を描くことができると思います。
このベクトル図を基に考えて見ると良いと思います。

2.送電電力と同期化力
送電線の抵抗が無視できる送電線において，発電機内部電圧及び無限大母線電圧の大きさ$ \ V_{1} \ $，$ \ V_{2} \ $とそれらの位相差$ \ \delta \ $並びに発電機から送電線にかけてのリアクタンスの総和$ \ X \ $を用いると，送電電力$ \ P \ $は，
\[
\begin{eqnarray}
P&=&\frac {V_{1}V_{2}}{X}\sin \delta \\[ 5pt ] \end{eqnarray}
\] となり，同期化力$ \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta } \ $は，
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}\delta }&=&\frac {V_{1}V_{2}}{X}\cos \delta \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　一機無限大母線系統の定態安定性

【解答】

(1)解答：ト
題意より，解答候補は（ト）上昇，（ル）低下，になると思います。ワンポイント解説「1.並行$ \ 2 \ $回線送電線での開放前後の発電機電圧」の通り，片回線が開放されると，リアクタンスが大きくなるので，発電機電圧は大きく上昇することになります。

(2)解答：ヨ
題意より，解答候補は（イ）後者の方が長い，（ヨ）前者の方が長い，になると思います。ワンポイント解説「2.送電電力と同期化力」の通り，同期化力は相差角$ \ \delta \ $が小さい方が大きくなるので，位相差が大きくなる開放時の方が同期化力は小さくなり，電力動揺は大きくなります。

(3)解答：チ
題意より，解答候補は（ニ）$\displaystyle P=\frac {V_{1}\cos \delta -V_{2}}{X}V_{2}$，（ホ）$\displaystyle P=\frac {V_{1}\sin \delta -V_{2}}{X}V_{2}$，（ヘ）$\displaystyle P=\frac {V_{1}V_{2}}{X}\cos \delta $，（チ）$\displaystyle P=\frac {V_{1}V_{2}}{X}\sin \delta $，になると思います。ワンポイント解説「2.送電電力と同期化力」の通り，送電電力は$\displaystyle P=\frac {V_{1}V_{2}}{X}\sin \delta $で求められます。

(4)解答：ヌ
題意より，解答候補は（リ）小さい，（ヌ）大きい，になると思います。ワンポイント解説「1.並行$ \ 2 \ $回線送電線での開放前後の発電機電圧」の通り，定常状態で比較すると，投入時に対して開放後の$ \ \delta \ $の値の方が大きくなります。

(5)解答：ロ
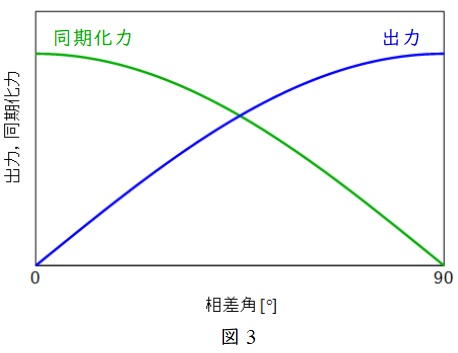
題意より，解答候補は（ロ）同期化力係数，（ハ）系統定数，（ワ）制動力係数，（カ）慣性定数，になると思います。図3に示すように開放後並びに投入時の定常状態における$ \ P-\delta \ $カーブの接線の傾きとは同期化力と言います。