【問題】
【難易度】★★★★★(難しい)
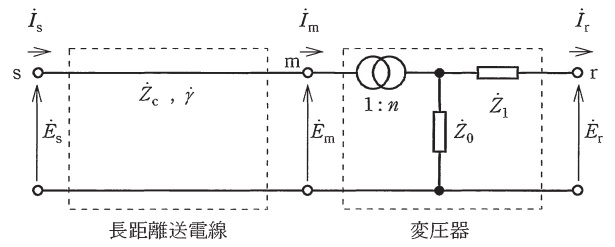
次の文章は,図に示す長距離送電線と変圧器が直列に接続された送電系統の四端子定数に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
長距離送電線の四端子定数は\( \ \fbox { (1) } \ \)モデルから求められる。長距離送電線の\( \ \fbox { (2) } \ \)を\( \ {\dot Z}_{\mathrm {c}} \ \),\( \ \fbox { (3) } \ \)を\( \ \dot \gamma \ \),送電線路の長さを\( \ l \ \)とし,変圧器は変圧比を\( \ 1 : n \ \),励磁インピーダンスを\( \ {\dot Z}_{0} \ \),漏れインピーダンスを\( \ {\dot Z}_{1} \ \)とする。
また,\( \ {\dot E}_{\mathrm {S}} \ \)及び\( \ {\dot I}_{\mathrm {S}} \ \),\( \ {\dot E}_{\mathrm {m}} \ \)及び\( \ {\dot I}_{\mathrm {m}} \ \),\( \ {\dot E}_{\mathrm {r}} \ \)及び\( \ {\dot I}_{\mathrm {r}} \ \)はそれぞれ端子\( \ \mathrm {s} \ \),\( \ \mathrm {m} \ \),\( \ \mathrm {r} \ \)の相電圧及び電流であり,
\[
\begin{bmatrix} {\dot E}_{\mathrm {s}} \\ {\dot I}_{\mathrm {s}} \end{bmatrix} = \begin{bmatrix} {\dot A}_{1} & {\dot B}_{1} \\ {\dot C}_{1} & {\dot D}_{1} \end{bmatrix} \begin{bmatrix} {\dot E}_{\mathrm {m}} \\ {\dot I}_{\mathrm {m}} \end{bmatrix},\begin{bmatrix} {\dot E}_{\mathrm {m}} \\ {\dot I}_{\mathrm {m}} \end{bmatrix} = \begin{bmatrix} {\dot A}_{2} & {\dot B}_{2} \\ {\dot C}_{2} & {\dot D}_{2} \end{bmatrix} \begin{bmatrix} {\dot E}_{\mathrm {r}} \\ {\dot I}_{\mathrm {r}} \end{bmatrix},\begin{bmatrix} {\dot E}_{\mathrm {s}} \\ {\dot I}_{\mathrm {s}} \end{bmatrix} = \begin{bmatrix} \dot A & \dot B \\ \dot C & \dot D \end{bmatrix} \begin{bmatrix} {\dot E}_{\mathrm {r}} \\ {\dot I}_{\mathrm {r}} \end{bmatrix}
\]
である。
長距離送電線の四端子定数のうち\( \ {\dot A}_{1} \ \),\( \ {\dot B}_{1} \ \)は
\[
{\dot A}_{1}=\cosh \dot \gamma l,{\dot B}_{1}=\fbox { (4) }
\]
となる。次に変圧器の四端子定数のうち\( \ {\dot B}_{2} \ \),\( \ {\dot D}_{2} \ \)は
\[
{\dot B}_{2}=\frac {{\dot Z}_{1}}{n},{\dot D}_{2}=\fbox { (5) }
\]
となる。次に送電系統全体の四端子定数のうち\( \ \dot C \ \)は
\[
\dot C =\frac {\sinh \dot \gamma l}{n\times {\dot Z}_{\mathrm {c}}}+\frac {n \times \cosh \dot \gamma l}{{\dot Z}_{0}}
\]
となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {1}{n}\left( 1+ \frac {{\dot Z}_{0}}{{\dot Z}_{1}}\right) &(ロ)& 分布定数 &(ハ)& -{\dot Z}_{\mathrm {c}}\cosh \dot \gamma l \\[ 5pt ]
&(ニ)& n\left( 1+ \frac {{\dot Z}_{1}}{{\dot Z}_{0}}\right) &(ホ)& 線路インピーダンス &(ヘ)& 伝搬定数 \\[ 5pt ]
&(ト)& 特性インピーダンス &(チ)& {\dot Z}_{\mathrm {c}}\sinh \dot \gamma l &(リ)& n\left( 1+ \frac {{\dot Z}_{0}}{{\dot Z}_{1}}\right) \\[ 5pt ]
&(ヌ)& {\dot Z}_{\mathrm {c}}\cosh \dot \gamma l &(ル)& 伝達インピーダンス &(ヲ)& 位相速度 \\[ 5pt ]
&(ワ)& 伝搬速度 &(カ)& 集中定数 &(ヨ)& 非線形 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
この問題はこれまで慣例的に二種では分布定数回路は出題されないとされてきたものを覆すような問題となっています。一種受験者であれば難なく解ける問題となりますが,二種受験者にとってはとても厳しい問題となったと思います。
1.基本的な回路の四端子定数
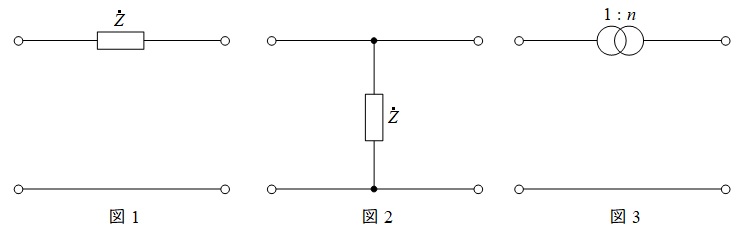
図1~図3の四端子定数は以下の通りとなります。
\[
\begin{eqnarray}
\begin{bmatrix} 1 & \dot Z \\ 0 & 1 \end{bmatrix} (図1) \\[ 5pt ]
\begin{bmatrix} 1 & 0 \\ \frac {1}{\dot Z} & 1 \end{bmatrix} (図2) \\[ 5pt ]
\begin{bmatrix} \frac {1}{n} & 0 \\ 0 & n \end{bmatrix} (図3) \\[ 5pt ]
\end{eqnarray}
\]
※それぞれの送電端電圧と受電端電圧の関係を求めれば導出することができますが,試験では暗記しておいた方が良いと思います。
2.分布定数回路の送電端電圧・電流と受電端電圧・電流の関係
長距離送電線では線路の特性インピーダンスや伝搬定数を無視することはできず,分布定数回路として扱います。線路の特性インピーダンスを\( \ {\dot Z}_{\mathrm {c}} \ \),伝搬定数を\( \ \dot \gamma \ \),線路の長さを\( \ l \ \)とすると,
\[
\begin{eqnarray}
\begin{bmatrix} {\dot E}_{\mathrm {s}} \\ {\dot I}_{\mathrm {s}} \end{bmatrix} &=& \begin{bmatrix} \cosh \dot \gamma l & {\dot Z}_{\mathrm {c}}\sinh \dot \gamma l \\ \displaystyle \frac {1}{{\dot Z}_{\mathrm {c}}}\sinh \dot \gamma l & \cosh \dot \gamma l \end{bmatrix} \begin{bmatrix} {\dot E}_{\mathrm {r}} \\ {\dot I}_{\mathrm {r}} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ロ
長距離送電線では,短距離送電線で用いられる一般的な集中定数回路の計算を用いず,分布定数回路にて求めます。
(2)解答:ト
長距離送電線の\( \ {\dot Z}_{\mathrm {c}} \ \)は特性インピーダンスと言います。
(3)解答:ヘ
長距離送電線の\( \ \dot \gamma \ \)を伝搬定数と言います。
(4)解答:チ
ワンポイント解説「2.分布定数回路の送電端電圧・電流と受電端電圧・電流の関係」の通り,長距離送電線の\( \ {\dot B}_{1} \ \)は,
\[
{\dot Z}_{\mathrm {c}}\sinh \dot \gamma l
\]
となります。
(5)解答:ニ
ワンポイント解説「1.基本的な回路の四端子定数」の通り,問題図の変圧器部の四端子定数は,
\[
\begin{eqnarray}
\begin{bmatrix} \frac {1}{n} & 0 \\ 0 & n \end{bmatrix}\begin{bmatrix} 1 & 0 \\ \frac {1}{\dot Z_{0}} & 1 \end{bmatrix} \begin{bmatrix} 1 & {\dot Z}_{1} \\ 0 & 1 \end{bmatrix} &=& \begin{bmatrix} \frac {1}{n} & 0 \\ \frac {n}{{\dot Z}_{0}} & n \end{bmatrix} \begin{bmatrix} 1 & {\dot Z}_{1} \\ 0 & 1 \end{bmatrix} \\[ 5pt ]
&=& \begin{bmatrix} \frac {1}{n} & \frac {{\dot Z}_{1}}{n} \\ \frac {n}{{\dot Z}_{0}} & n\left( \frac {{\dot Z}_{1}}{{\dot Z}_{0}}+1\right) \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは