《機械》〈自動制御〉[H19:問3]一巡伝達関数のベクトル軌跡に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，一巡伝達関数$ \ \displaystyle G(s)=\frac {K}{s\left( s+1\right) \left( s+4\right) } \ $のベクトル軌跡に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる語句，式又は数値を解答群の中から選び，その記号をマークシートに記入しなさい。

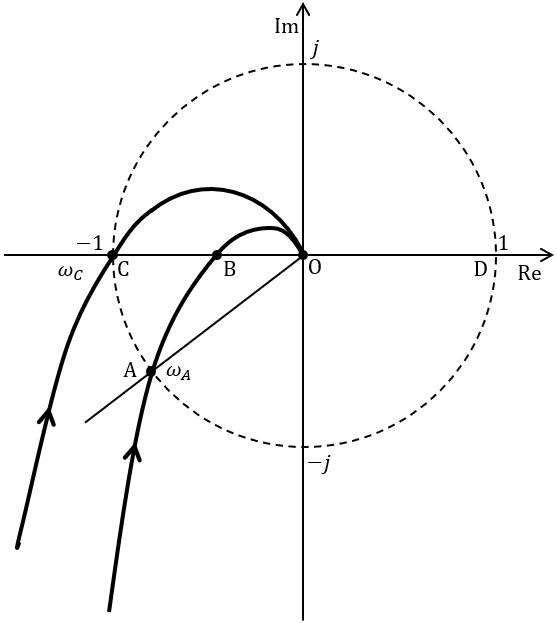
図のベクトル軌跡において，位相余裕は図中の角，$ \ \fbox {　（１）　} \ [ $度$ ] \ $で与えられ，ゲイン余裕は$ \ \fbox {　（２）　} \ \mathrm {[dB]} \ $で与えられる。位相余裕とゲイン余裕は，閉ループ制御系設計において$ \ \fbox {　（３）　} \ $に関する設計指標であり，これらが小さくなるようにゲイン$ \ K \ $を変化させると，閉ループ制御系のゲイン特性のピーク値（$ \ \mathrm {M} \ $ピーク）は$ \ \fbox {　（４）　} \ $。$ \ K \ $が$ \ \fbox {　（５）　} \ $のとき，ベクトル軌跡は実軸上の$ \ \mathrm {C} \ $点$ \ \left( -1+j0 \right) \ $と交差する。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　\angle \mathrm {OCA}　　　　　&（ロ）&　\overline {\mathrm {OB}}　　　　　&（ハ）&　安定性 \\[ 5pt ] &（ニ）&　減少する　　　　　&（ホ）&　20　　　　　&（ヘ）&　速応性 \\[ 5pt ] &（ト）&　\angle \mathrm {AOC}　　　　　&（チ）&　40　　　　　&（リ）&　-20 \log \overline {\mathrm {OB}} \\[ 5pt ] &（ヌ）&　変化しない　　　　　　　&（ル）&　定常特性　　　　　　　&（ヲ）&　増大する \\[ 5pt ] &（ワ）&　10　　　　　　　&（カ）&　\angle \mathrm {DOA}　　　　　&（ヨ）&　20 \log \overline {\mathrm {OB}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

ナイキスト線図を用いた安定性評価に関する問題です。
どちらかというと二次試験で出題されやすい内容で一次試験で出題されることは少ない分野です。二次試験の勉強を事前にされていた方であれば高得点が狙えた可能性がありますが，全くされていない方であると厳しい問題であったかもしれません。

1.システムの安定性と速応性
システムの安定性と速応性は，読んで字のごとくどれだけシステムが安定しているか，どれだけ速く応答するかの指標です。ゲイン余裕や位相余裕，ゲイン交差角周波数や位相交差角周波数は，開ループ周波数伝達関数を用いたボード線図とナイキスト線図により理解することができます。
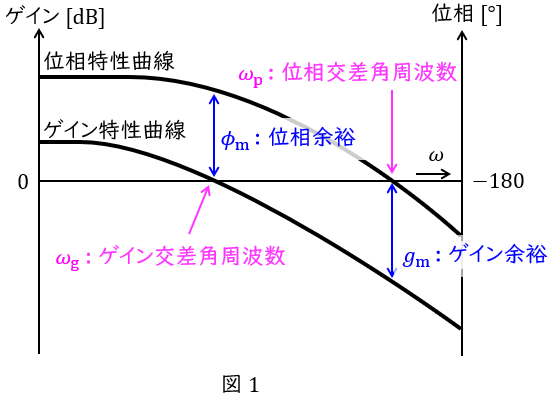
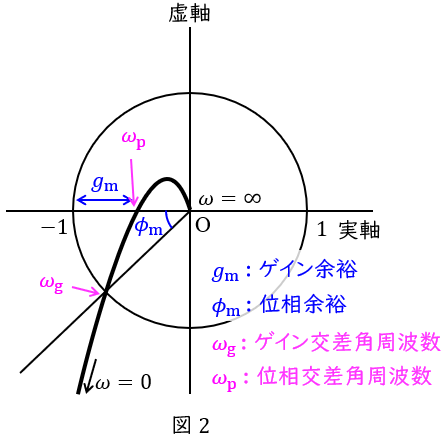
ボード線図は，横軸に角周波数，縦軸にゲインと位相の二軸としたグラフで図1のように描くことができ，ナイキスト線図は実軸と虚軸の平面において，角周波数を$ \ 0 \ $から$ \ \infty \ $まで変化させたときのベクトル軌跡で図2のように描くことができます。
安定性の仕様を与える尺度としてはゲイン余裕$ \ g_{\mathrm {m}} \ $と位相余裕$ \ \phi _{\mathrm {m}} \ $があり，ゲイン余裕は位相が$ \ -180 \ [°] \ $のときの$ \ 0 \ \mathrm {[dB]} \ $との差で，位相余裕はゲインが$ \ 0 \ \mathrm {[dB]} \ $のときの$ \ -180 \ [°] \ $との位相差となります。ボード線図とナイキスト線図においては図1及び図2に示すような相互関係があります。
速応性の仕様を与える尺度としてはゲイン交差角周波数$ \ \omega _{\mathrm {g}} \ $と位相交差角周波数$ \ \omega _{\mathrm {p}} \ $があり，ゲイン交差角周波数はゲインが$ \ 0 \ \mathrm {[dB]} \ $のときの角周波数，位相交差角周波数は位相が$ \ -180 \ [°] \ $のときの角周波数となります。ボード線図とナイキスト線図においては図1及び図2に示すような相互関係になります。

【解答】

(1)解答：ト
題意より，解答候補は（イ）$ \ \angle \mathrm {OCA} \ $，（ト）$ \ \angle \mathrm {AOC} \ $，（カ）$ \ \angle \mathrm {DOA} \ $，になると思います。
ワンポイント解説「1.システムの安定性と速応性」の通り，位相余裕は$ \ \angle \mathrm {AOC} \ [ $度$ ] \ $で与えられます。

(2)解答：リ
題意より，解答候補は（ロ）$ \ \overline {\mathrm {OB}} \ $，（リ）$ \ -20 \log \overline {\mathrm {OB}} \ $，（ヨ）$ \ 20 \log \overline {\mathrm {OB}} \ $，になると思います。
ワンポイント解説「1.システムの安定性と速応性」の通り，ゲイン余裕は線分$ \ \overline {\mathrm {BC}}=\overline {\mathrm {OC}}-\overline {\mathrm {OB}} \ $になりますが，$ \ \mathrm {dB} \ $で表すと，
\[
\begin{eqnarray}
20\log _{10} \left| \overline {\mathrm {OC}}\right| -20\log _{10} \left| \overline {\mathrm {OB}}\right| &=&20\log _{10} 1 -20\log _{10} \left| \overline {\mathrm {OB}}\right| \\[ 5pt ] &=&0-20\log _{10} \left| \overline {\mathrm {OB}}\right| \\[ 5pt ] &=&-20\log _{10} \left| \overline {\mathrm {OB}}\right| \ \mathrm {[dB]} \\[ 5pt ] \end{eqnarray}
\] と求められます。

(3)解答：ハ
題意より，解答候補は（ハ）安定性，（ヘ）速応性，（ル）定常特性，になると思います。
ワンポイント解説「1.システムの安定性と速応性」の通り，位相余裕とゲイン余裕は安定性に関する指標となります。

(4)解答：ヲ
題意より，解答候補は（ニ）減少する，（ヌ）変化しない，（ヲ）増大する，になると思います。
ワンポイント解説「1.システムの安定性と速応性」の通り，位相余裕やゲイン余裕が小さくなるとシステムとしてはやや不安定なシステムと変化するため，閉ループ制御系のゲイン特性のピーク値（$ \ \mathrm {M} \ $ピーク）は増大するようになります。

(5)解答：ホ
題意より，解答候補は（ホ）$ \ 20 \ $，（チ）$ \ 40 \ $，（ワ）$ \ 10 \ $，になると思います。
$ \ \displaystyle G(s)=\frac {K}{s\left( s+1\right) \left( s+4\right) } \ $の周波数伝達関数$ \ G(j\omega ) \ $は，
\[
\begin{eqnarray}
G(j\omega ) &=&\frac {K}{j\omega \left( 1+j\omega \right) \left( 4+j\omega \right) } \\[ 5pt ] &=&\frac {K}{j\omega \left( 4-\omega ^{2}+j5\omega \right) } \\[ 5pt ] &=&\frac {K}{-5\omega ^{2}+j\omega \left( 4-\omega ^{2}\right) } \\[ 5pt ] \end{eqnarray}
\] となり，実軸上の$ \ \mathrm {C} \ $点$ \ \left( -1+j0 \right) \ $と交差するとき，虚部は$ \ 0 \ $ですから，
\[
\begin{eqnarray}
\omega _{C} \left( 4-\omega _{C}^{2}\right) &=&0 \\[ 5pt ] 4-\omega _{C}^{2} &=&0　\left( ∵\omega _{C}＞0 \right) \\[ 5pt ] \left( 2+\omega _{C} \right) \left( 2-\omega _{C} \right) &=&0 \\[ 5pt ] \omega _{C} &=&2 \ \mathrm {[rad / s]}　\left( ∵\omega _{C}＞0 \right) \\[ 5pt ] \end{eqnarray}
\] となり，このときの実部は$ \ -1 \ $なので，
\[
\begin{eqnarray}
\frac {K}{-5\omega _{C} ^{2} } &=&-1 \\[ 5pt ] K&=&5\omega _{C} ^{2} \\[ 5pt ] &=&5\times 2 ^{2} \\[ 5pt ] &=&20 \\[ 5pt ] \end{eqnarray}
\] と求められます。