Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,三相誘導電動機の不平衡運転に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な語句又は式を解答群の中から選び,その記号をマークシートに記入しなさい。
誘導電動機に接続されている三相電源の供給電圧が不平衡になった場合,対称座標法を用いて正相分と逆相分とに分けて電流を計算し,重ねの理(重ね合わせの理)によって実際の電流を求めることができる。
正相電圧に対して誘導電動機が滑り\( \ s \ \)で運転しているとき,逆相電圧に対しては滑り\( \ \fbox { (1) } \ \)で運転している。したがって,誘導電動機の\( \ \fbox { (2) } \ \)等価回路は,\( \ \fbox { (3) } \ \)等価回路における滑り\( \ s \ \)を滑り\( \ \fbox { (1) } \ \)に置き換えたものとなる。
また,電動機トルクについては,正相電流によるトルクに対して逆相電流によるトルクは\( \ \fbox { (4) } \ \)であるから,三相電源の供給電圧が平衡である場合のトルクに比して,不平衡である場合にはその大きさは減少する。
通常は三相運転であるが,もし三相電源と誘導電動機を接続する線路の\( \ 1 \ \)線が断線した異常な場合には,他の\( \ 2 \ \)線から電圧・電流の供給を受けて,\( \ \fbox { (5) } \ \)として運転を継続する。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& 2-s &(ロ)& 直 軸 &(ハ)& 逆方向 \\[ 5pt ]
&(ニ)& 単相同期電動機 &(ホ)& 常に零 &(ヘ)& 単相誘導電動機 \\[ 5pt ]
&(ト)& 1-s &(チ)& 正 相 &(リ)& 静止座標 \\[ 5pt ]
&(ヌ)& -s &(ル)& 零 相 &(ヲ)& 同じ方向 \\[ 5pt ]
&(ワ)& 逆 相 &(カ)& 横 軸 &(ヨ)& 二重給電誘導電動機 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
三相誘導電動機の不平衡運転に関する問題です。
対称座標法の理解は二次試験で稀に出題される内容です。勉強効率を考えると優先度は低いですが,本問の内容を本質的に理解されたい方は学習すると良いかと思います。
1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は,
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,同期角速度\( \ \omega _{\mathrm {s}} \ \mathrm {[rad / s]} \ \)は,
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ]
&=&\frac {2\pi }{60}\cdot \frac {120f}{p} \\[ 5pt ]
&=&\frac {4\pi f}{p} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \),回転子の回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
と定義されます。これを整理すると,
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ]
N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ]
&=&N_{\mathrm {s}}\left( 1-s \right) \\[ 5pt ]
\end{eqnarray}
\]
と同期速度から回転速度が導出できます。
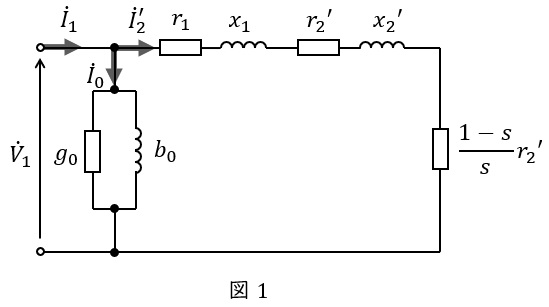
3.三相誘導電動機の\( \ \mathrm {L} \ \)形等価回路
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
【解答】
(1)解答:イ
題意より解答候補は,(イ)\( \ 2-s \ \),(ト)\( \ 1-s \ \),(ヌ)\( \ -s \ \),になると思います。
ワンポイント解説「2.誘導機の滑り\( \ s \ \)」の通り,逆相電圧に対する滑り\( \ s^{\prime } \ \)は同期速度を\( \ -N_{\mathrm {s}} \ \)として考えれば良いので,
\[
\begin{eqnarray}
s^{\prime } &=&\frac {-N_{\mathrm {s}}-N}{-N_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {N_{\mathrm {s}}+N}{N_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {N_{\mathrm {s}}+N_{\mathrm {s}}\left( 1-s \right) }{N_{\mathrm {s}}} \\[ 5pt ]
&=&1+\left( 1-s \right) \\[ 5pt ]
&=&2-s \\[ 5pt ]
\end{eqnarray}
\]
となります。
(2)解答:ワ
題意より解答候補は,(ロ)直軸,(チ)正相,(ル)零相,(ワ)逆相,(カ)横軸,になると思います。
誘導電動機において,滑り\( \ s \ \)を\( \ 2-s \ \)に置き換えた回路を逆相等価回路といいます。
(3)解答:チ
題意より解答候補は,(ロ)直軸,(チ)正相,(ル)零相,(ワ)逆相,(カ)横軸,になると思います。
誘導電動機において,\( \ \mathrm {L} \ \)形等価回路等の一般的な等価回路を逆相等価回路に対して正相等価回路といいます。
(4)解答:ハ
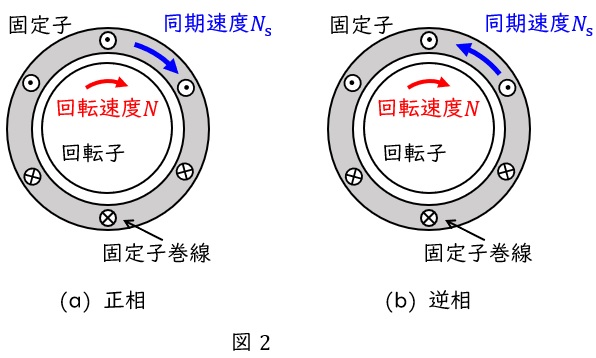
題意より解答候補は,(ハ)逆方向,(ホ)常に零,(ヲ)同じ方向,になると思います。
逆相電流によるトルクは,正相電流に対して逆方向となります。こちらは計算しても導出可能ですが,下図のように固定子磁界が逆方向に回転した場合に回転子のトルクがどのようになるかイメージした方がわかりやすいかと思います。
(5)解答:ヘ
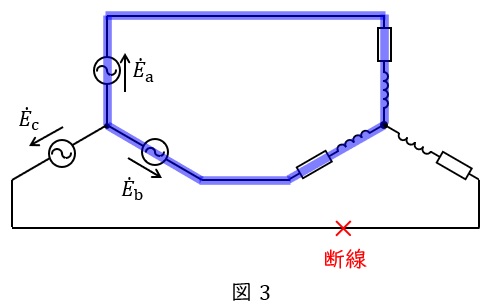
題意より解答候補は,(ニ)単相同期電動機,(ヘ)単相誘導電動機,(ヨ)二重給電誘導電動機,になると思います。
図3(\( \ \mathrm {Y} \ \)結線の例)に示すように,\( \ 1 \ \)線が断線した場合には他の\( \ 2 \ \)線から電圧・電流の供給を受け,単相誘導電動機として運転を継続することになります。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは