《機械》〈パワーエレクトロニクス〉[H21:問6]直流チョッパの動作に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，直流チョッパに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な語句又は式を解答群の中から選び，その記号をマークシートに記入しなさい。

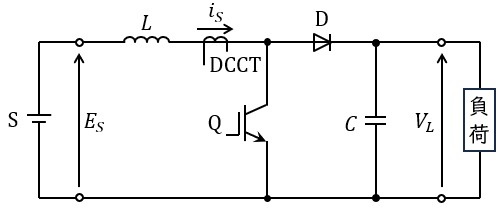
図に示すチョッパは，入出力電圧の関係で分類すると\( \ \fbox {　 （１） 　} \ \)チョッパである。この図のチョッパに用いられているオンオフ制御バルブデバイス（スイッチングデバイス。 以下デバイスと略す。）\( \ \mathrm {Q} \ \)は，その図記号から\( \ \fbox {　 （２） 　} \ \)である。

デバイス\( \ \mathrm {Q} \ \)は，\( \ T \ \)の周期で，\( \ T_{\mathrm {on}} \ \)の時間はオンし，残りの\( \ T_{\mathrm {off}} \ \)の時間はオフする。デバイス\( \ \mathrm {Q} \ \)をオンすると，リアクトル\( \ L \ \)に流れている電源電流\( \ i_{S} \ \)は，電源\( \ \mathrm {S} \ \)→リアクトル\( \ L \ \)→デバイス\( \ \mathrm {Q} \ \)→電源\( \ \mathrm {S} \ \)の経路で流れ，リアクトル\( \ L \ \)に蓄えられるエネルギーが増加する。

デバイス\( \ \mathrm {Q} \ \)をオフすると，リアクトル\( \ L \ \)に蓄えられたエネルギーが負荷側に放出され，電源電流\( \ i_{S} \ \)は，電源\( \ \mathrm {S} \ \)→ リアクトル\( \ L \ \)→ダイオード\( \ \mathrm {D} \ \)→コンデンサ\( \ C \ \)・負荷→電源\( \ \mathrm {S} \ \)の経路を流れる。このとき，電源電流\( \ i_{S} \ \)のリプルが十分に小さく一定値\( \ I_{S} \ \)と見なせると仮定すると，ダイオード\( \ \mathrm {D} \ \)に流れる電流\( \ i_{D} \ \)の平均値\( \ I_{D} \ \)は，次式となる。
\[
\begin{eqnarray}
I_{D}&=& \ \fbox {　 （３） 　} \ \\[ 5pt ] \end{eqnarray}
\] チョッパの出力電圧は，コンデンサ\( \ C \ \)で十分に平滑化されて一定値と見なせるものとし，その値を\( \ V_{L} \ \)とする。チョッパ内での損失がないと仮定すれば，電源\( \ \mathrm {S} \ \)からチョッパへの入力電力\( \ E_{S}\times I_{S} \ \)と，チョッパから負荷への出力電力\( \ V_{L}\times I_{D} \ \)とは等しくなり，これと上記の式から出力電圧\( \ V_{L} \ \)は次式となる。
\[
\begin{eqnarray}
V_{L}&=& \ \fbox {　 （４） 　} \ \\[ 5pt ] \end{eqnarray}
\] なお，出力電圧制御を行うときは，出力回路にコンデンサがあることからコンデンサの充電電圧を変化させようとしたときの悪影響などを防止するため，マイナループ制御として\( \ \fbox {　 （５） 　} \ \)制御を加えて行う。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\mathrm {IGBT}　　　　　&（ロ）&　E_{S}\times \frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}　　　　　　　　&（ハ）&　I_{S}\times \frac {T_{\mathrm {on}}}{T} \\[ 5pt ] &（ニ）&　昇降圧　　　　　&（ホ）&　I_{S}\times \frac {T_{\mathrm {off}}}{T}　　　　　&（ヘ）&　降　圧 \\[ 5pt ] &（ト）&　電　流　　　　　&（チ）&　I_{S}\times \frac {T_{\mathrm {off}}}{T_{\mathrm {on}}}　　　　　&（リ）&　\mathrm {MOSFET} \\[ 5pt ] &（ヌ）&　電　力　　　　　&（ル）&　E_{S}\times \frac {T}{T_{\mathrm {off}}}　　　　　&（ヲ）&　電　圧 \\[ 5pt ] &（ワ）&　昇　圧　　　　　&（カ）&　E_{S}\times \frac {T}{T_{\mathrm {on}}}　　　　　&（ヨ）&　\mathrm {GTO} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

直流チョッパに関する問題です。
各チョッパの回路図は描けなければならないわけではありませんが，回路を見た状態で判断できるようになる必要があります。
以下に各チョッパの内容を記載しますので，本問と直接関係のないチョッパの内容も理解しておいて下さい。

1.降圧チョッパ
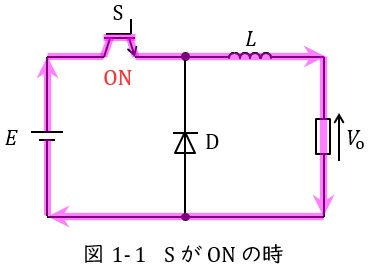
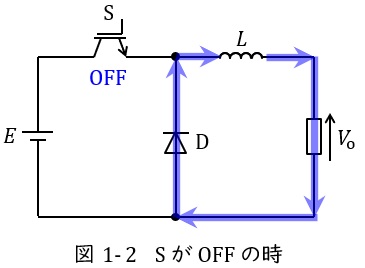
図1-1及び図1-2は降圧チョッパの例を示します。
スイッチ\( \ \mathrm {S} \ \)がオンになると，図1-1のように電源からの電流はスイッチ\( \ \mathrm {S} \ \)を通り，リアクトル\( \ L \ \)側に電流が流れますが，ダイオード\( \ \mathrm {D} \ \)は逆向きなので電流が流れません。
スイッチ\( \ \mathrm {S} \ \)がオフになると，図1-2のように電源から電流は流れず，リアクトル\( \ L \ \)に蓄えられているエネルギーから出力側と還流ダイオード\( \ \mathrm {D} \ \)に電流が流れます。
したがって降圧チョッパの出力電圧の平均値\( \ V_{\mathrm {o}} \ \)は，スイッチのオン時間を\( \ T_{\mathrm {on}} \ \)，オフ時間を\( \ T_{\mathrm {off}} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {o}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] で求められます。このとき，\( \ E \ \)の係数
\[
\begin{eqnarray}
\gamma &=&\frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}} \\[ 5pt ] \end{eqnarray}
\] を通流率といいます。

2.昇圧チョッパ
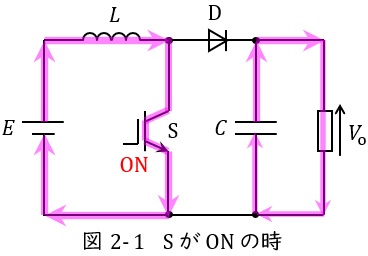
図2-1及び図2-2に昇圧チョッパの例を示します。
スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {ON} \ \)時は図2-1のように導通し，電源\( \ E \ \)からリアクトル\( \ L \ \)にエネルギー\( \ EIT_{\mathrm {on}} \ \)が蓄えられ，出力側はコンデンサ\( \ C \ \)から電荷が供給されます。
スイッチ\( \ \mathrm {OFF} \ \)時は図2-2のように導通し，リアクトル\( \ L \ \)に蓄えられたエネルギー\( \ \displaystyle L\frac {\mathrm {d}i}{\mathrm {d}t}IT_{\mathrm {off}} \ \)が放出されます。定常状態では蓄えられるエネルギーと放出するエネルギーが等しいので，
\[
\begin{eqnarray}
EIT_{\mathrm {on}}&=&L\frac {\mathrm {d}i}{\mathrm {d}t}IT_{\mathrm {off}} \\[ 5pt ] ET_{\mathrm {on}}&=&L\frac {\mathrm {d}i}{\mathrm {d}t}T_{\mathrm {off}} \\[ 5pt ] L\frac {\mathrm {d}i}{\mathrm {d}t}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] となります。また回路方程式は，
\[
\begin{eqnarray}
E+L\frac {\mathrm {d}i}{\mathrm {d}t}&=&V_{\mathrm {o}} \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
E+L\frac {\mathrm {d}i}{\mathrm {d}t}&=&V_{\mathrm {o}} \\[ 5pt ] E+\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E&=&V_{\mathrm {o}} \\[ 5pt ] V_{\mathrm {o}}&=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] となります。

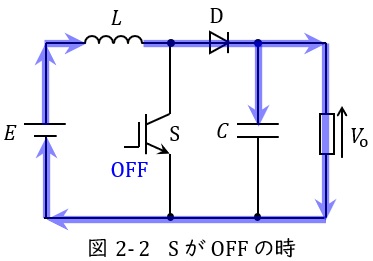
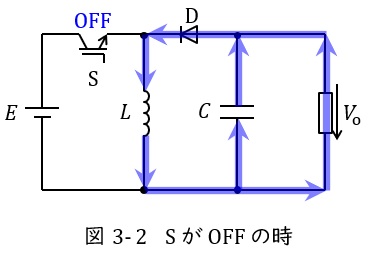
3.昇降圧チョッパ
スイッチ\( \ \mathrm {S} \ \)がオンのとき，図3-1のように電源からの電流はスイッチ\( \ \mathrm {S} \ \)を通り，リアクトル\( \ L \ \)側にエネルギーが蓄えられますが，ダイオード\( \ D \ \)は逆向きなので電流が流れません。また，コンデンサ\( \ C \ \)に蓄えられている電荷が出力側に流れます。
スイッチ\( \ \mathrm {S} \ \)がオフになると，図3-2のように電源から電流は流れず，リアクトル\( \ L \ \)に蓄えられていたエネルギーが放出され，コンデンサ\( \ C \ \)と出力側に電流が流れます。
したがって，コンデンサ\( \ C \ \)の容量が十分に大きければ，出力電流はほぼ一定の値となります。
定常状態においてはリアクトルに蓄えられるエネルギーと放出されるエネルギーが等しいので，スイッチ\( \ \mathrm {S} \ \)のオン時間を\( T_{\mathrm {on}} \ \)，オフ時間を\( T_{\mathrm {off}} \ \)，出力電圧\( \ V_{\mathrm {0}} \ \)とすると，
\[
\begin{eqnarray}
EIT_{\mathrm {on}} &=& V_{\mathrm {0}} IT_{\mathrm {off}} \\[ 5pt ] ET_{\mathrm {on}} &=&V_{\mathrm {0}} T_{\mathrm {off}} \\[ 5pt ] V_{\mathrm {0}} &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] となり，通流率\( \ \displaystyle \gamma =\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ \)を用いて表すと，
\[
\begin{eqnarray}
v_{\mathrm {0}} &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E \\[ 5pt ] &=&\frac {\displaystyle \frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}{\displaystyle \frac {T_{\mathrm {off}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}E \\[ 5pt ] &=&\frac {\displaystyle \frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}{\displaystyle \frac {T_{\mathrm {on}}+T_{\mathrm {off}}-T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}E \\[ 5pt ] &=&\frac {\displaystyle \frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}{\displaystyle 1-\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}E \\[ 5pt ] &=&\frac {\gamma }{\displaystyle 1-\gamma }E \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ワ
題意より解答候補は，（ニ）昇降圧，（ヘ）降圧，（ワ）昇圧，になると思います。
ワンポイント解説「2.昇圧チョッパ」の通り，問題図のチョッパは昇圧チョッパとなります。

(2)解答：イ
題意より解答候補は，（イ）\( \ \mathrm {IGBT} \ \)，（リ）\( \ \mathrm {MOSFET} \ \)，（ヨ）\( \ \mathrm {GTO} \ \)，になると思います。
\( \ \mathrm {Q} \ \)の図記号は\( \ \mathrm {IGBT} \ \)となります。\( \ \mathrm {MOSFET} \ \)と\( \ \mathrm {GTO} \ \)（ゲートターンオフサイリスタ）の図記号は以下の通りです。参考程度に見ておいて下さい。

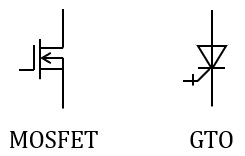
(3)解答：ホ
題意より解答候補は，（ハ）\( \ \displaystyle I_{S}\times \frac {T_{\mathrm {on}}}{T} \ \)，（ホ）\( \ \displaystyle I_{S}\times \frac {T_{\mathrm {off}}}{T} \ \)，（チ）\( \ \displaystyle I_{S}\times \frac {T_{\mathrm {off}}}{T_{\mathrm {on}}} \ \)，になると思います。
問題文及びワンポイント解説「2.昇圧チョッパ」の通り，ダイオードに導通するのはデバイス\( \ \mathrm {Q} \ \)がオフのときなので，電流値が一定値\( \ I_{S} \ \)と見なせると，平均値\( \ I_{D} \ \)は，
\[
\begin{eqnarray}
I_{D}&=&\displaystyle I_{S}\times \frac {T_{\mathrm {off}}}{T}\\[ 5pt ] \end{eqnarray}
\] となります。

(4)解答：ル
題意より解答候補は，（ロ）\( \ \displaystyle E_{S}\times \frac {T_{\mathrm {on}}}{T_{\mathrm {off}}} \ \)，（ル）\( \ \displaystyle E_{S}\times \frac {T}{T_{\mathrm {off}}} \ \)，（カ）\( \ \displaystyle E_{S}\times \frac {T}{T_{\mathrm {on}}} \ \)，になると思います。
\( \ E_{S}I_{S}=V_{L}I_{D} \ \)より，
\[
\begin{eqnarray}
E_{S}I_{S}&=&V_{L} I_{S}\times \frac {T_{\mathrm {off}}}{T}\\[ 5pt ] E_{S}&=&V_{L} \times \frac {T_{\mathrm {off}}}{T}\\[ 5pt ] V_{L}&=&E_{S}\times \frac {T}{T_{\mathrm {off}}}\\[ 5pt ] \end{eqnarray}
\] となります。

※　本解答は問題文のヒントなしで導出できるようになる必要があります。

(5)解答：ト
題意より解答候補は，（ト）電流，（ヌ）電力，（ヲ）電圧，になると思います。
ワンポイント解説「2.昇圧チョッパ」の通り，コンデンサにはオンとオフのタイミングで充放電を繰り返し，出力電圧制御を行うときは悪影響を防止するため，マイナループ制御として電流制御を加え制御を安定化させます。