《機械》〈パワーエレクトロニクス〉[H22:問3]電圧形自励インバータに関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，電圧形自励インバータに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切な語句又は式を解答群の中から選びなさい。

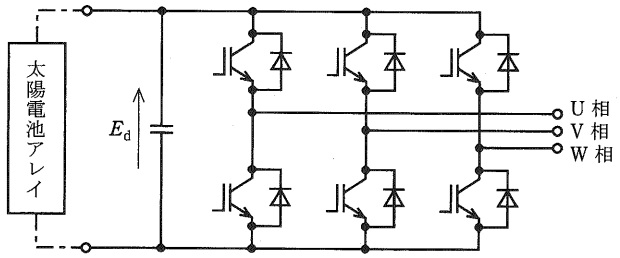
図は，$ \ \mathrm {PWM} \ $（パルス幅変調）制御された三相ブリッジ接続の電圧形自励インバータであり，その直流電圧は$ \ E_{\mathrm {d}} \ $である。三相の商用周波数の正弦波信号波を数キロヘルツの$ \ \fbox {　（１）　} \ $の搬送波と比較してパルス幅変調して各相の電圧を発生させたとき，相電圧の基本波の振幅は$ \ \fbox {　（２）　} \ $（信号波振幅の搬送波振幅に対する比）$ \ k \ \left( k≦1 \right) \ $に比例して変化し，$ \ k=1 \ $のときは$ \displaystyle \frac {E_{\mathrm {d}}}{2} \ $となる。このことから，線間電圧の基本波実効値は$ \ \fbox {　（３）　} \ $となる。ただし，デッドタイムなどの影響は考慮しないものとする。

このインバータの交流側は連系リアクトルを介して系統に連系し，直流側は太陽電池アレイを接続して太陽光発電を行うものとする。太陽電池によって$ \ \fbox {　（４）　} \ $が確立してからインバータを始動し，交流電圧の位相及び振幅を系統に一致させてから系統に連系して運転する。始動後は，最大電力点追従$ \ \left( \mathrm {MPPT} \right) \ $制御などによって設定された値になるように$ \ \fbox {　（４）　} \ $を制御する。

そのためには，太陽電池出力が大きくなったときはインバータの出力有効電力を大きくするように制御する。出力有効電力を大きくしたとき, インバータの出力電圧の基本波の位相は系統電圧に対して$ \ \fbox {　（５）　} \ $ことになる。

一方，無効電力については$ \ 0 \ $として力率が$ \ 1 \ $になるようにすることが多い。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　直流電圧　　　　　&（ロ）&　正弦波　　　　　&（ハ）&　三角波 \\[ 5pt ] &（ニ）&　直流電流　　　　　&（ホ）&　方形波　　　　　&（ヘ）&　\frac {E_{\mathrm {d}}}{\sqrt {2}}k \\[ 5pt ] &（ト）&　\frac {\sqrt {3}E_{\mathrm {d}}}{2\sqrt {2}}k　　　　　&（チ）&　ひずみ率　　　　　&（リ）&　\frac {E_{\mathrm {d}}}{2\sqrt {2}}k \\[ 5pt ] &（ヌ）&　変調率　　　　　　&（ル）&　一致する　　　　　&（ヲ）&　より遅れる \\[ 5pt ] &（ワ）&　波形率　　　　　&（カ）&　直流電力　　　　　　　&（ヨ）&　より進む \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電圧形自励インバータに関する問題で，前半はインバータの概念に関するパワーエレクトロニクスらしい問題ですが，後半は太陽光発電の$ \ \mathrm {MPPT} \ $制御に関する問題となっています。
前半の$ \ \mathrm {PWM} \ $制御は二次試験にも出題されやすい内容となっていますので，必ず理解しておくようにしましょう。

1.最大電力点追従制御（$ \ \mathrm {MPPT} \ $制御）
太陽光の日射量の変化による太陽電池の出力変動に応じて，最大電力を得られるようにする制御です。
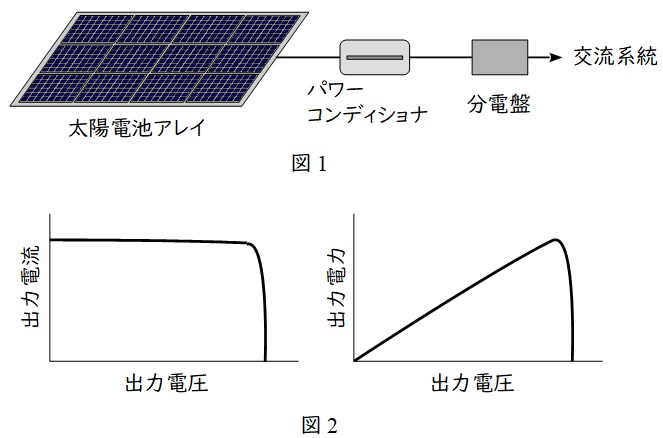
太陽光が地球に降り注ぐ光エネルギーのエネルギー密度は$ \ 1 \ \mathrm {m^{2}} \ $当たり約$ \ 1 \ \mathrm {kW} \ $程度で，太陽電池セルでは$ \ 1 \ \mathrm {V} \ $程度かそれ以下の直流電圧しか出力されないので図1のように直並列して太陽電池アレイとして，パワーコンディショナを介して交流にし系統に連系します。
日射強度一定時の太陽電池の出力電流・出力電圧特性は図2左のようになるため，出力電力は電圧に応じて異なり出力電力・出力電圧特性は図2右のようになります。最大電力点追従制御（$ \ \mathrm {MPPT} \ $制御）は，パワーコンディショナにおいて太陽電池から常に最大の電力を取り出すような制御を行うもので，この最大点を追従する制御となります。

2.$ \ \mathrm {PWM} \ $制御と変調率
$ \ \mathrm {PWM} \ $制御はパルス幅変調制御を意味し，出力の交流電圧をパルス幅で制御する方法となります。
出力電圧は交流電源の搬送波と信号波の大きさの比較により行います。
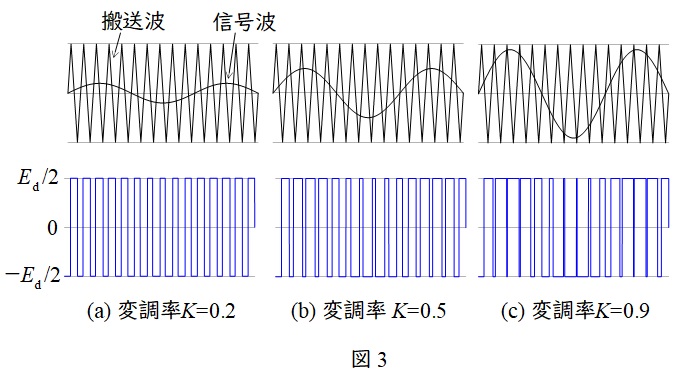
変調率は搬送波と信号波の比率をいい，図3のように搬送波と信号波の比率を変化させることで，出力電圧のパルス幅を変化させることができます。

【解答】

(1)解答：ハ
題意より解答候補は，（ロ）正弦波，（ハ）三角波，（ホ）方形波，になると思います。
ワンポイント解説「2.$ \ \mathrm {PWM} \ $制御と変調率」の通り，$ \ \mathrm {PWM} \ $制御では三角波の搬送波と比較してパルス幅変調させて電圧を発生させます。

(2)解答：ヌ
題意より解答候補は，（チ）ひずみ率，（ヌ）変調率，（ワ）波形率，になると思います。
ワンポイント解説「2.$ \ \mathrm {PWM} \ $制御と変調率」の通り，信号波振幅の搬送波振幅に対する比を変調率といいます。ひずみ率は基本波に対するの全高調波の割合，波形率は実効値の平均値に対する比をいいます。

(3)解答：ト
題意より解答候補は，（ヘ）$ \ \displaystyle \frac {E_{\mathrm {d}}}{\sqrt {2}}k \ $，（ト）$ \ \displaystyle \frac {\sqrt {3}E_{\mathrm {d}}}{2\sqrt {2}}k \ $，（リ）$ \ \displaystyle \frac {E_{\mathrm {d}}}{2\sqrt {2}}k \ $，になると思います。
相電圧の振幅が$ \ \displaystyle \frac {E_{\mathrm {d}}}{2}k \ $なので，実効値は$ \ \displaystyle \frac {E_{\mathrm {d}}}{2\sqrt {2}}k \ $となり，線間電圧は$ \ \displaystyle \frac {\sqrt {3}E_{\mathrm {d}}}{2\sqrt {2}}k \ $となります。

(4)解答：イ
題意より解答候補は，（イ）直流電圧，（ニ）直流電流，（カ）直流電力，になると思います。
インバータは太陽電池によって直流電圧が確立してから始動します。

(5)解答：ヨ
題意より解答候補は，（ル）一致する，（ヲ）より遅れる，（ヨ）より進む，になると思います。
インバータの出力有効電力を大きくすると，インバータの出力電圧の基本波の位相は系統電圧に対してより進むことになります。こちらの空欄は非常に専門性が高いので，とりあえずは覚えておくと良いでしょう。