《機械》〈回転機〉[H28:問1] 他励直流電動機の始動に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，他励直流電動機の始動に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

他励直流電動機では，界磁電流$ \ I_{\mathrm{f}} \ $が作る磁場中にある電機子巻線に電流$ \ i_{\mathrm{a}} \ $が流れると，電機子には$ \ KI_{\mathrm{f}}i_{\mathrm{a}} \ $で表される$ \ \fbox {　（１）　} \ $が発生する。$ \ K \ $は比例係数である。
以下では，$ \ I_{\mathrm{f}} \ $を一定とし，電機子反作用を考えないで$ \ KI_{\mathrm{f}} \ $は一定とする。一方，この磁場中を電機子巻線導体が$ \ \omega _{\mathrm{m}} \ $の角速度で回転することによって，電機子巻線には，$ \ KI_{\mathrm{f}}\omega _{\mathrm{m}} \ $で表される$ \ \fbox {　（２）　} \ $が発生する。
したがって，電機子電圧を$ \ v_{\mathrm{a}} \ $とし，$ \ i_{\mathrm{a}} \ $と$ \ \omega _{\mathrm{m}} \ $を時間$ \ t \ $の関数とすると電機子回路での関係式は，
\[
v_{\mathrm{a}}\left( t\right) =R_{\mathrm{a}}i_{\mathrm{a}}\left( t\right) +KI_{\mathrm{f}}\omega _{\mathrm{m}}\left( t\right) 　・・・・・・・・・・・・①
\] と表せる。ここで，電機子巻線インダクタンスを無視する。$ \ R_{\mathrm{a}} \ $は電機子抵抗であり，ここでは一定とする。
また，電機子の回転運動を表す関係式は，負荷のトルクを$ \ T_{\mathrm{L}} \ $一定(摩擦トルクは無視する)とすると，
\[
J\frac {\mathrm {d}\omega _{\mathrm{m}}\left( t\right) }{\mathrm {d}t}=KI_{\mathrm{f}} i_{\mathrm{a}}\left( t\right) -T_{\mathrm{L}}　・・・・・・・・・・・・・②
\] と表せる。電動機の$ \ \fbox {　（１）　} \ $と負荷トルクの差によって，電動機は加速あるいは減速される。係数$ \ J \ $は$ \ \fbox {　（３）　} \ $であり，以下では一定とする。
今，無負荷($ \ T_{\mathrm{L}}=0 \ $)とし，時刻$ \ t=0 \ $で電機子端子に一定の直流電圧$ \ E \ $を加えて電動機を始動したとき，①式は，
\[
v_{\mathrm{a}}\left( t\right) =E=R_{\mathrm{a}}i_{\mathrm{a}}\left( t\right) +KI_{f}\omega _{\mathrm{m}}\left( t\right) 　・・・・・・・・・・③
\] となり，電機子電流と回転角速度は時間とともに変化する。②式を用いて時刻$ \ t \ $における回転角速度$ \ \omega _{\mathrm{m}}\left( t\right) \ $を求めるために，積分変数を$ \ \tau \ $とおいて記述すると，
\[
\omega _{\mathrm{m}}\left( t\right) =\frac {KI_{\mathrm{f}}}{J}\int ^{t}_{0}i_{\mathrm{a}}\left( \tau \right) \mathrm {d}\tau 　・・・・・・・・・・・・・・④
\] となる。これを③式に代入して$ \ \omega _{\mathrm{m}}\left( t\right) \ $を消去すると，
\[
E=R_{\mathrm{a}}i_{\mathrm{a}}\left( t\right) +\frac {\left( KI_{\mathrm{f}}\right) ^{2}}{J}\int ^{t}_{0}i_{\mathrm{a}}\left( \tau \right) \mathrm {d}\tau 　・・・・・・・・・・⑤
\] とできる。ここで，$ \ \displaystyle \frac {J}{\left( KI_{\mathrm{f}}\right) ^{2}}=C_{\mathrm{m}} \ $は等価的な静電容量とみなせて，電機子回路は図のようなスイッチ$ \ \mathrm {S} \ $を含む等価回路に置き換えることができる。

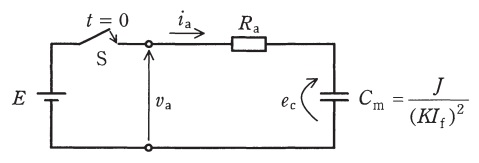
始動時の電流変化$ \ i_{\mathrm{a}}\left( t\right) \ $は，等価回路において$ \ t=0 \ $でスイッチ$ \ \mathrm {S} \ $を閉じたときの電流変化として求められる。
ここで，
\[
Q\left( t\right) =\int ^{t}_{0}i_{\mathrm{a}}\left( \tau \right) \mathrm {d}\tau 　・・・・・・・・・・・・・・・・・・⑥
\] とおけば，$ \ Q\left( t\right) \ $は，時刻$ \ t \ $における$ \ C_{\mathrm{m}} \ $に充電された電荷を表し，その充電電圧$ \ \displaystyle e_{\mathrm{C}}\left( t\right) =\frac {Q\left( t\right) }{C_{\mathrm{m}}} \ $は，電動機の$ \ \fbox {　（２）　} \ $に対応する。静電容量$ \ C_{\mathrm{m}} \ $に蓄えられたエネルギー$ \ \displaystyle W_{\mathrm{C}}\left( t\right) = \frac {1}{2}C_{\mathrm{m}}\left[ e_{\mathrm{C}}\left( t\right) \right] ^{2} \ $は電動機の回転子の$ \ \fbox {　（４）　} \ $に相当する。
⑤式から，始動時の電流の時間変化$ \ i_{\mathrm{a}}\left( t \right) \ $を求めると，
\[
i_{\mathrm{a}}\left( t \right) =\fbox {　（５）　}　・・・・・・・・・・・・・・・・・・・⑦
\] となる。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　角運動量　　　&（ロ）&　回転運動エネルギー　　　&（ハ）&　制動力 \\[ 5pt ] &（ニ）&　\frac {E}{R_{\mathrm{a}}}\exp \left( -\frac {t}{C_{\mathrm{m}}R_{\mathrm{a}}}\right) 　　　&（ホ）&　制動エネルギー　　　&（ヘ）&　慣性モーメント \\[ 5pt ] &（ト）&　トルク　　　&（チ）&　回転子半径　　　&（リ）&　誘導起電力 \\[ 5pt ] &（ヌ）&　抵抗損失　　　&（ル）&　\frac {E}{R_{\mathrm{a}}}\exp \left( -\frac {R_{\mathrm{a}}}{C_{\mathrm{m}}}t\right)　　　&（ヲ）&　\frac {E}{R_{\mathrm{a}}}\left[ 1-\exp \left( -\frac {t}{C_{\mathrm{m}}R_{\mathrm{a}}}\right) \right] \\[ 5pt ] &（ワ）&　質　量　　　&（カ）&　同期化力　　　&（ヨ）&　変圧器起電力
\end{eqnarray}
\]

【ワンポイント解説】

本問は問題文が長く一見難しそうですが，見た目ほど難しくはなく，電動機の基本的な公式を理解しているかと，基本的なラプラス変換の回路が解けるかを問う問題となっています。

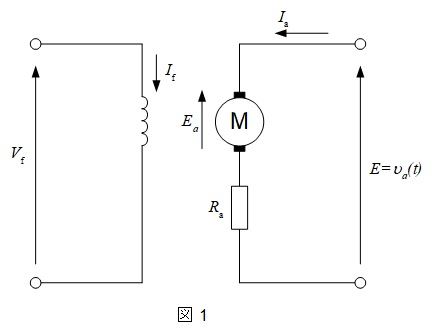
1.直流他励電動機の等価回路

\[
\begin{eqnarray}
&E&&:&端子電圧　　　　　　&E_{\mathrm{a}}&&:&誘導起電力　　　　　　&I_{\mathrm{a}}&&:&電機子電流 \\[ 5pt ] &R_{\mathrm{a}}&&:&電機子抵抗　&V_{\mathrm{f}}&&:&界磁電圧　&I_{\mathrm{f}}&&:&界磁電流
\end{eqnarray}
\]

2.微分と積分のラプラス変換
$ \ f(t) \ $のラプラス変換を$ \ F(s) \ $とすると，
\[
\begin{eqnarray}
\mathcal{L}[f^{’}(t)]&=&sF(s)-f(0) \\[ 5pt ] \mathcal{L}\left[ \int ^{t}_{0}f(\tau )\mathrm {d}\tau \right] &=&\frac {1}{s}F(s) \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ト
直流機のトルクは磁束$ \ \phi \ $と電機子電流$ \ i_{\mathrm{a}} \ $に比例します。磁束$ \ \phi \ $は界磁電流$ \ I_{\mathrm{f}} \ $に比例するので，$ \ KI_{\mathrm{f}}i_{\mathrm{a}} \ $は直流機に発生するトルクとなります。

(2)解答：リ
誘導起電力は題意で与えられた$ \ KI_{f}\omega _{\mathrm{m}} \ $となります。①式と等価回路図1からも，誘導起電力であることが分かります。

(3)解答：ヘ
$ \ J \ $は慣性モーメントと言います。

(4)解答：ロ
図より，$ \ e_{\mathrm{C}} \ $は誘導起電力となり，そのエネルギー$ \ \displaystyle W_{\mathrm{C}}\left( t\right) = \frac {1}{2}C_{\mathrm{m}}\left[ e_{\mathrm{C}}\left( t\right) \right] ^{2} \ $は回転運動エネルギーとなります。

(5)解答：ニ
題意から⑤式は，
\[
\begin{eqnarray}
E&=&R_{\mathrm{a}}i_{\mathrm{a}}\left( t\right) +\frac {1}{C_{\mathrm{m}}}\int ^{t}_{0}i_{\mathrm{a}}\left( \tau \right) \mathrm {d}\tau \\[ 5pt ] \end{eqnarray}
\] となるので，両辺をラプラス変換すると，
\[
\begin{eqnarray}
\frac {E}{s}&=&R_{\mathrm{a}}I_{\mathrm{a}}\left( s\right) +\frac {I_{\mathrm{a}}\left( s\right) }{C_{\mathrm{m}}s} \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ I_{\mathrm{a}}\left( s\right) \ $について整理すると，
\[
\begin{eqnarray}
I_{\mathrm{a}}\left( s\right) &=&\frac {EC_{\mathrm{m}}}{C_{\mathrm{m}}R_{\mathrm{a}}s+1} \\[ 5pt ] &=&\frac {E}{R_{\mathrm{a}}}\cdot \frac {1}{s+\frac {1}{C_{\mathrm{m}}R_{\mathrm{a}}}} \\[ 5pt ] \end{eqnarray}
\] となる。これをラプラス逆変換すると，
\[
\begin{eqnarray}
i_{\mathrm{a}}\left( t\right) &=&\frac {E}{R_{\mathrm{a}}}\exp \left( -\frac {t}{C_{\mathrm{m}}R_{\mathrm{a}}}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。