《機械》〈照明〉[H29:問6] 照度の定義と逆2乗の法則との関係に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，照度の定義と逆$ \ 2 \ $乗の法則との関係に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

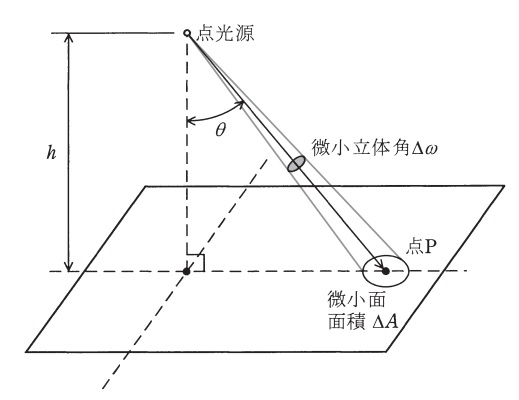
図に示すように，点光源が水平な机上面上の高さ$ \ h \ $にあり，その鉛直角$ \ \theta \ $方向の微小立体角$ \ \Delta \omega \ $内を光束$ \ \mathit {\Phi } \ $が通過している。ここで，点光源とは，光源から照射を受ける面までの距離に比べて，光源の大きさが無視できる程度に小さなものをいう。逆$ \ 2 \ $乗の法則による照度計算は，この点光源を前提としている。
この条件において，ある点$ \ P \ $の水平面照度$ \ E_{\mathrm {h}} \ $が，その点$ \ P \ $に対応する微小面の平均照度$ \ E_{\mathrm {av}} \ $であることを以下に説明する。
まず，光源からある方向に向かう光束の単位立体角当たりの割合を$ \ \fbox {　（１）　} \ $という。逆2乗の法則による机上面上の点$ \ P \ $の水平面照度$ \ E_{\mathrm {h}} \ $は，逆$ \ 2 \ $乗の法則に従って，光度$ \ I \ $，高さ$ \ h \ $，鉛直角$ \ \theta \ $を用いて表すと$ \ \fbox {　（２）　} \ $となる。点光源の鉛直角$ \ \theta \ $(点$ \ P \ $)方向の光度$ \ I \ $は，$ \ \Delta \omega \ $と$ \ \mathit {\Phi } \ $とを用いて表すと$ \ \fbox {　（３）　} \ $で求まるので，$ \ h \ $と$ \ \theta \ $とが分かれば$ \ E_{\mathrm {h}} \ $を求めることができる。
次に，微小立体角$ \ \Delta \omega \ $が机上面に投影して作る微小面の面積$ \ \Delta A \ $の平均照度$ \ E_{\mathrm {av}} \ $を求める。照度の定義に従えば，$ \ \Delta A \ $の平均照度$ \ E_{\mathrm {av}} \ $は$ \ \fbox {　（４）　} \ $で表せる。$ \ \Delta A \ $は微小立体角$ \ \Delta \omega \ $，高さ$ \ h \ $，鉛直角$ \ \theta \ $を用いて表すと$ \ \fbox {　（５）　} \ $となるので，これを$ \ \fbox {　（４）　} \ $に代入すれば$ \ E_{\mathrm {av}} \ $を求めることができる。
この$ \ E_{\mathrm {av}} \ $を求める関係に，$ \ I=\fbox {　（３）　} \ $を代入して$ \ \mathit {\Phi } \ $，$ \ \Delta \omega \ $を消去し，光度$ \ I \ $を用いて表せば$ \ \fbox {　（２）　} \ $となる。よって，ある点の水平面照度$ \ E_{\mathrm {h}} \ $は，その点に対応する微小面の平均照度$ \ E_{\mathrm {av}} \ $と同一である。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\Delta \omega \cdot \cos^{3}\theta }{h^{2}}　　　&（ロ）&　\frac {\Delta \omega \cdot h^{2}}{\cos^{3}\theta }　　　&（ハ）&　\frac {I\cdot \cos^{3}\theta }{h^{2}} \\[ 5pt ] &（ニ）&　光束発散度　　　&（ホ）&　\frac {\Delta \omega \cdot h^{2}}{\cos\theta }　　　&（ヘ）&　\frac {I\cdot \cos^{2}\theta }{h^{2}} \\[ 5pt ] &（ト）&　光度　　　&（チ）&　\frac {\Delta A}{\mathit {\Phi }}　　　&（リ）&　\mathit {\Phi } \cdot \Delta \omega \\[ 5pt ] &（ヌ）&　\mathit {\Phi } \cdot \Delta A　　　&（ル）&　\frac {I\cdot \cos\theta }{h^{2}}　　　&（ヲ）&　輝度 \\[ 5pt ] &（ワ）&　\frac {\Delta \omega }{\mathit {\Phi }}　　　&（カ）&　\frac {\mathit {\Phi }}{\Delta \omega }　　　&（ヨ）&　\frac {\mathit {\Phi }}{\Delta A }
\end{eqnarray}
\]

【ワンポイント解説】

照明計算の定義と逆$ \ 2 \ $乗の法則を理解していれば難しい問題ではありませんが，二次試験では出題されず毎年出題されるとは限らない分野なので，受験生があまり勉強しない分野となっています。また，本問の内容はすべて定義と法則なので，暗記するしかありません。しかし，勉強していればそれほど難しい問題は出題されにくく確実に得点源となる分野なので，機械科目が苦手な方は是非とも勉強しておきたい分野となります。

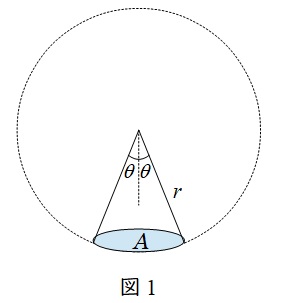
1.立体角$ \ \omega \ $
図1において，$ \ \displaystyle \omega =\frac {A}{r^{2}}\mathrm {[sr]} \ $を立体角と言います。

2.光束$ \ \mathit {\Phi } \ $
光の量で単位はルーメン$ \ \mathrm {[lm]} \ $となります。電磁気で言うと磁束のようなものです。

3.光度$ \ I \ $
光束を立体角で割ったものです。微小立体角$ \ \Delta \omega \ $に含まれる光束を$ \ \mathit {\Phi } \ $とすると，光度$ \ I \ $は，
\[
I= \frac {\mathit {\Phi } }{\Delta \omega}　\mathrm {[cd]}
\] となります。

4.照度$ \ E \ $
均一に照射された面の明るさで，微小面積$ \ \Delta A \ $に入射する光束を$ \ \mathit {\Phi } \ $とすると，
\[
E=\frac {\mathit {\Phi }}{\Delta A}\mathrm {[lx]}
\] となります。

5.逆$ \ 2 \ $乗の法則
照度の定義式$ \ \displaystyle E=\frac {\mathit {\Phi }}{\Delta A} \ $に光度の定義式$ \ \displaystyle I= \frac {\mathit {\Phi }}{\Delta \omega} \ $と立体角の定義$ \ \Delta A=\Delta \omega r^{2} \ $を代入すると，
\[
E=\frac {\mathit {\Phi }}{\Delta A}=\frac {I\Delta \omega}{\Delta \omega r^{2}}=\frac {I}{r^{2}}
\] となります。

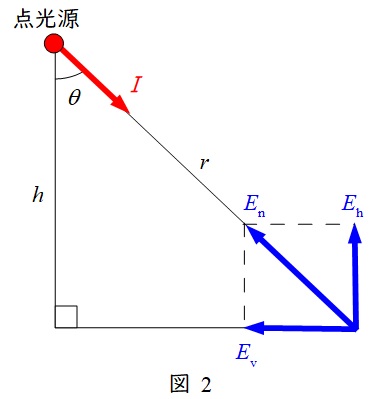
6.水平面照度と鉛直面照度
図2における$ \ E_{\mathrm {n}} \ $を法線照度，$ \ E_{\mathrm {h}} \ $を水平面照度，$ \ E_{\mathrm {v}} \ $を鉛直面照度と言い，以下のような関係があります。
\[
E_{\mathrm {n}}=\frac {I}{r^{2}}=\frac {I\cdot \cos^{2}\theta }{h^{2}}
\] \[
E_{\mathrm {h}}=E_{\mathrm {n}}\cos\theta =\frac {I\cdot \cos^{3}\theta }{h^{2}}
\] \[
E_{\mathrm {v}}=E_{\mathrm {n}}\sin\theta =\frac {I\cdot \sin\theta \cos^{2}\theta }{h^{2}}
\]

【解答】

(1)解答：ト
ワンポイント解説より，光束を単位立体角で割ったものを光度と言います。

(2)解答：ハ
ワンポイント解説「6.水平面照度と鉛直面照度」の通り，水平面照度$ \ E_{\mathrm {h}} \ $は，
\[
E_{\mathrm {h}}=\frac {I\cdot \cos^{3}\theta }{h^{2}}
\] となります。

(3)解答：カ
ワンポイント解説「3.光度$ \ I \ $」の通り，光度$ \ I \ $は，
\[
I= \frac {\mathit {\Phi }}{\Delta \omega}
\] となります。

(4)解答：ヨ
ワンポイント解説「4.照度$ \ E \ $」の通り，照度$ \ E \ $は，
\[
E=\frac {\mathit {\Phi }}{\Delta A}
\] となります。

(5)解答：ロ
ワンポイント解説「1.立体角$ \ \omega \ $」の式に，$ \ A=\Delta A \cos\theta \ $，$ \ \displaystyle r=\frac {h}{\cos\theta } \ $を代入すると，
\[
\Delta \omega =\frac {\Delta A \cos\theta }{\displaystyle \left( \frac {h}{\cos\theta }\right) ^{2}}
\] となり，$ \ \Delta A \ $について整理すると，
\[
\Delta A=\frac {\Delta \omega \cdot h^{2}}{\cos^{3}\theta }
\] となります。