《機械》〈回転機〉[R01:問1]三相誘導電動機の特性に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，誘導電動機に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

三相誘導電動機の一次巻線に三相交流電源を接続すると回転磁界が発生する。回転磁界と回転子の回転速度に差があると，回転子の二次巻線に\( \ \fbox {　 （１） 　} \ \)が流れ，回転磁界との間でトルクが生じる。このとき，発生するトルクは，回転磁界と回転子の回転速度の差を\( \ \fbox {　 （２） 　} \ \)方向に働く。

二極機のギャップに生じる磁束密度分布を正弦波状と仮定し，回転角速度を\( \ \omega \ \)とすると，任意の位置\( \ \theta \ \)で観測される磁束密度は，
\[
\begin{eqnarray}
B\left( \theta ，t\right) &=&B_{\mathrm {m}} \cos \left( \theta -\omega t\right) 　　　　　　　　　　　&・・・・・・・・・・　①& \\[ 5pt ] \end{eqnarray}
\] と表すことができる。ただし，\( \ B_{\mathrm {m}} \ \)は最大磁束密度である。①式は，\( \ \theta =\fbox {　 （３） 　} \ \)の位置に最大磁束密度\( \ B_{\mathrm {m}} \ \)が現れることを示している。

一方，二極の純単相誘導電動機の磁束密度分布は，
\[
\begin{eqnarray}
B^{\prime }\left( \theta ，t\right) &=&B^{\prime }_{\mathrm {m}} \cos \left( \theta \right) \cos \left( \omega t \right)　　　　　　　　　&・・・・・・・・・・　②& \\[ 5pt ] \end{eqnarray}
\] と表せる。この場合，\( \ \theta =\fbox {　 （４） 　} \ \)の位置で最大値となる正弦波状\( \ \cos \left( \theta \right) \ \)の磁束密度分布となり，その大きさは\( \ \cos \left( \omega t \right) \ \)で変化する。このような磁束は，回転磁界に対して，交番磁界と呼ばれる。②式を書き換えると，磁束密度分布は，
\[
\begin{eqnarray}
B^{\prime }\left( \theta ，t\right) &=&\frac {B^{\prime }_{\mathrm {m}}}{2} \cos \left( \theta -\omega t \right) +\fbox {　 （５） 　}　&・・・・・・・・・・　③& \\[ 5pt ] \end{eqnarray}
\] と二つの成分の和で表すことができる。③式の第1項は①式と同じ方向に回転する回転磁界であり，第2項はそれとは逆方向に回転する回転磁界である。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　減少させる　　　　　&（ロ）&　維持する　　　　　&（ハ）&　0 \\[ 5pt ] &（ニ）&　\frac {B^{\prime }_{\mathrm {m}}}{2} \cos \left( \theta +\omega t \right) 　　　　　&（ホ）&　\frac {B^{\prime }_{\mathrm {m}}}{2} \sin \left( \theta +\omega t \right)　　　　　&（ヘ）&　\frac {2\pi }{3} \\[ 5pt ] &（ト）&　漏れ電流　　　　　&（チ）&　\frac {\pi }{2}　　　　　　&（リ）&　-\omega t \\[ 5pt ] &（ヌ）&　\omega t　　　　　&（ル）&　2\omega t　　　　　&（ヲ）&　励磁電流 \\[ 5pt ] &（ワ）&　誘導電流　　　　　&（カ）&　増加させる　　　　　&（ヨ）&　\left[ -\frac {B^{\prime }_{\mathrm {m}}}{2} \cos \left( \theta +\omega t \right) \right] \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

(1)～(2)は誘導機の原理に関する問題で，(3)～(5)はほぼ数学に関する問題と言えます。3種では三角関数でここまで複雑な計算は少ないかもしれないですが，2種では本問程度の計算力が求められます。

1.加法定理
\[
\begin{eqnarray}
\sin \left( \alpha ±\beta \right) &=&\sin \alpha \cos \beta ±\cos \alpha \sin \beta \\[ 5pt ] \cos \left( \alpha ±\beta \right) &=&\cos \alpha \cos \beta ∓\sin \alpha \sin \beta \\[ 5pt ] \end{eqnarray}
\]

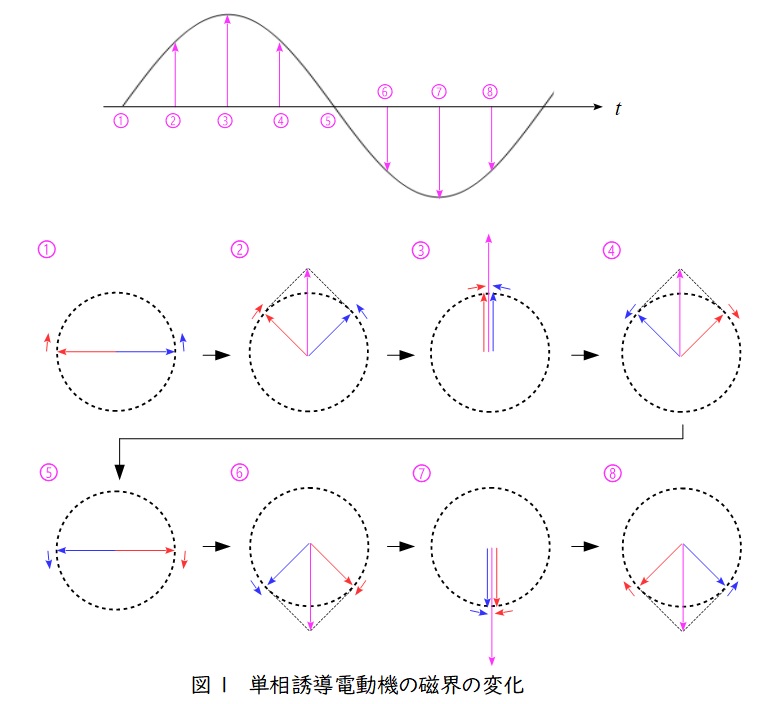
2.単相誘導電動機の磁界の変化
単相誘導電動機は単相の交番磁界により運転する電動機であり，単相の交番磁界は図１のように正方向の回転磁界（青矢印）と逆方向の回転磁界（赤矢印）に分けることができ，２つの回転磁界を合わせたものと考えることができます。
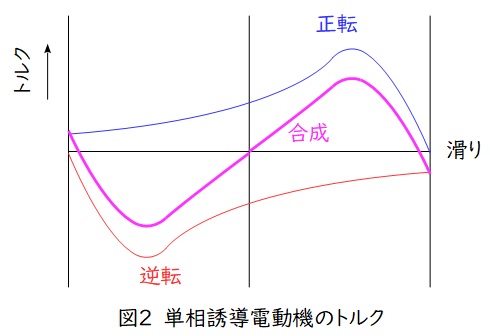
回転磁界によるトルク特性は図２の青矢印と赤矢印で表されるので，その合成トルクは紫矢印のようになり，始動時に回転磁界が発生せず，仮にどちらかに動いた場合にはそちら側にトルクがかかるようになることが分かります。

【解答】

(1)解答：ワ
題意より解答候補は，（ト）漏れ電流，（ヲ）励磁電流，（ワ）誘導電流，になると思います。二次巻線に流れるのは誘導電流です。

(2)解答：イ
題意より解答候補は，（イ）減少させる，（ロ）維持する，（カ）増加させる，になると思います。回転磁界と回転子の回転速度は差があるので，トルクはその差を減少させる方向に働きます。

(3)解答：ヌ
\( \ \cos \left( \theta -\omega t\right) \ \)は\( \ \theta -\omega t=0 \ \)の時最大値\( \ 1 \ \)となるので，
\[
\begin{eqnarray}
\theta &=&\omega t \\[ 5pt ] \end{eqnarray}
\] の時最大となる。

(4)解答：ハ
\( \ \cos \left( \theta \right) \ \)は\( \ \theta =0 \ \)の時最大値\( \ 1 \ \)となり，その大きさは\( \ \cos \left( \omega t \right) \ \)で変化します。

(5)解答：ニ
ワンポイント解説「1.加法定理」より，
\[
\begin{eqnarray}
\cos \left( \alpha +\beta \right) &=&\cos \alpha \cos \beta -\sin \alpha \sin \beta \\[ 5pt ] \cos \left( \alpha -\beta \right) &=&\cos \alpha \cos \beta +\sin \alpha \sin \beta \\[ 5pt ] \end{eqnarray}
\] であるから，左辺同士，右辺同士を足し合わせると，
\[
\begin{eqnarray}
\cos \left( \alpha +\beta \right) +\cos \left( \alpha -\beta \right) &=&2\cos \alpha \cos \beta \\[ 5pt ] \cos \alpha \cos \beta &=&\frac {1}{2}\left[ \cos \left( \alpha +\beta \right) +\cos \left( \alpha -\beta \right) \right] \\[ 5pt ] \end{eqnarray}
\] となる。したがって，②は，
\[
\begin{eqnarray}
B^{\prime }\left( \theta ，t\right) &=& \frac {B^{\prime }_{\mathrm {m}}}{2} \cos \left( \theta +\omega t \right) +\frac {B^{\prime }_{\mathrm {m}}}{2} \cos \left( \theta -\omega t \right) \\[ 5pt ] \end{eqnarray}
\] と求められる。