《機械》〈電熱〉[R02:問7]誘導加熱の原理及び諸定理に関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，誘導加熱に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

誘導加熱は，導電性の被加熱物を交番磁束中に置くことで生じる\( \ \fbox {　 （１） 　} \ \)によって被加熱物自体が発熱し，加熱される方式である。金属の溶解のほか，金属表面の焼入れなどに用いられている。

\( \ \fbox {　 （１） 　} \ \)として発生する熱量は，交番磁束の大きさ\( \ \fbox {　 （２） 　} \ \)する。このほか，交番磁束の周波数，被加熱物の透磁率及び導電率にも依存する。また，印加する交番磁束の周波数を\( \ \fbox {　 （３） 　} \ \)すると，発熱は被加熱物の表面近傍に集中するようになる。この現象は\( \ \fbox {　 （４） 　} \ \)によるものである。また，その指標として浸透深さがある。浸透深さは，透磁率と導電率の積\( \ \fbox {　 （５） 　} \ \)する。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　の平方根に比例 　　　　　&（ロ）&　の \ 2 \ 乗に比例　　　　　&（ハ）&　に反比例 \\[ 5pt ] &（ニ）&　ペルチェ効果　　　　　&（ホ）&　近接効果　　　　　&（ヘ）&　渦電流損 \\[ 5pt ] &（ト）&　高く　　　　　&（チ）&　一定に　　　　　&（リ）&　に比例 \\[ 5pt ] &（ヌ）&　機械損　　　　　&（ル）&　の \ 4 \ 乗に比例　　　　　&（ヲ）&　表皮効果 \\[ 5pt ] &（ワ）&　の平方根に反比例　　　　　　　&（カ）&　低く　　　　　&（ヨ）&　誘電損 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

誘導加熱に関する出題です。
毎年１問選択問題で出題されるかどうかという電熱の分野ですが，電熱の分野の中では誘導加熱と誘電加熱の出題頻度が高い傾向にあります。
あまり業務で使用されない方だとイメージしにくいかもしれませんが，IHクッキングヒーターのようなイメージで十分と思いますので，概要を理解しておくようにしましょう。

1.誘導加熱
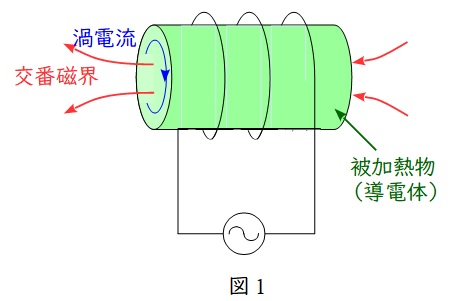
　交番磁界中に導電体を置くことによって，ファラデーの電磁誘導の法則により渦電流が生じ，その抵抗損（ジュール損）によって発熱します。オール電化のコンロ等はこの原理を利用しています。

2.電流の浸透深さ\( \ \delta \ \)
渦電流の値が表面の\( \ \mathrm {e}^{-1} \ \)倍 (約\( \ 0.368 \ \)倍)まで減少した時の深さを浸透深さ\( \ \delta \ \)と言い，角周波数を\( \ \omega \ \)，被加熱物の透磁率を\( \ \mu \ \)，抵抗率\( \ \rho \ \)が与えられているとすると，
\[
\begin{eqnarray}
\delta &=&\sqrt {\frac {2\rho }{\omega \mu }} \\[ 5pt ] \end{eqnarray}
\] となります。すなわち，角周波数（周波数）が低いほど，内部まで加熱することができることがわかります。

【関連する「電気の神髄」記事】

　　円筒導体における電流分布と表皮効果

【解答】

(1)解答：ヘ
題意より解答候補は，（ヘ）渦電流損，（ヌ）機械損，（ヨ）誘電損，になると思います。
ワンポイント解説「1.誘導加熱」の通り，誘導加熱は渦電流損を利用した加熱方法です。

(2)解答：ロ
題意より解答候補は，（イ）の平方根に比例，（ロ）の\( \ 2 \ \)乗に比例，（ハ）に反比例，（リ）に比例，（ル）の\( \ 4 \ \)乗に比例，（ワ）の平方根に反比例，になると思います。
変圧器の分野にて取り扱う公式ですが，渦電流損\( \ W_{\mathrm {e}} \ \)は，比例定数\( \ K_{\mathrm {e}} \ \)，周波数\( \ f \ \)，最大磁束密度\( \ B_{\mathrm {m}} \ \)，鉄板の厚さを\( \ t \ \)とすると，
\[
\begin{eqnarray}
W_{\mathrm {e}} &≒& K_{\mathrm {e}}\left( tfB_{\mathrm {m}}\right) ^{2} \\[ 5pt ] \end{eqnarray}
\] で求められ，交番磁束（∝磁束密度）の\( \ 2 \ \)乗に比例することが分かります。

(3)解答：ト
題意より解答候補は，（ト）高く，（チ）一定に，（カ）低く，になると思います。
ワンポイント解説「2.電流の浸透深さ\( \ \delta \ \)」の通り，周波数を高くすると発熱は被加熱物の表面近傍に集中するようになります。料理における強火と弱火のようなイメージで良いです。

(4)解答：ヲ
題意より解答候補は，（ニ）ペルチェ効果，（ホ）近接効果，（ヲ）表皮効果，になると思います。
周波数を高くすると発熱は被加熱物の表面近傍に集中する現象を表皮効果といいます。

(5)解答：ワ
題意より解答候補は，（イ）の平方根に比例，（ロ）の\( \ 2 \ \)乗に比例，（ハ）に反比例，（リ）に比例，（ル）の\( \ 4 \ \)乗に比例，（ワ）の平方根に反比例，になると思います。
ワンポイント解説「2.電流の浸透深さ\( \ \delta \ \)」の通り，浸透深さ\( \ \delta \ \)は，角周波数を\( \ \omega \ \)，被加熱物の透磁率を\( \ \mu \ \)，抵抗率\( \ \rho \ \)とすると，
\[
\begin{eqnarray}
\delta &=&\sqrt {\frac {2\rho }{\omega \mu }} \\[ 5pt ] \end{eqnarray}
\] となり，導電率\( \displaystyle \ \sigma =\frac {1}{\rho } \ \)なので，
\[
\begin{eqnarray}
\delta &=&\sqrt {\frac {2}{\omega \mu \sigma }} \\[ 5pt ] \end{eqnarray}
\] となるので，透磁率\( \ \mu \ \)及び導電率\( \ \sigma \ \)の積の平方根に反比例することが分かります。