《機械》〈パワーエレクトロニクス〉[R03:問2]ハーフブリッジ電圧形インバータの動作に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，インバータの動作に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

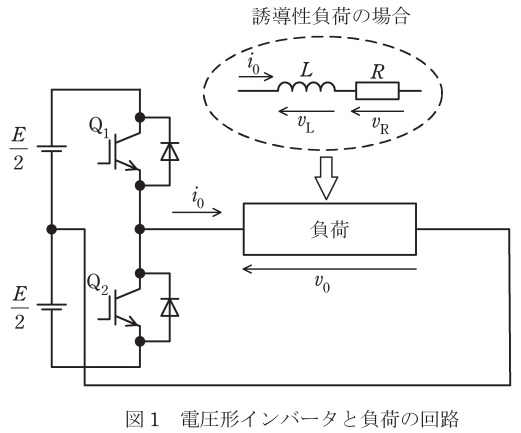
図1にハーフブリッジ電圧形インバータに負荷を接続した回路図を示す。図2には負荷にかかる交流電圧$ \ v_{0} \ $と負荷に流れる定常状態の交流電流$ \ i_{0} \ $の波形を示す。電圧形インバータでは，スイッチングデバイス$ \ \mathrm {Q}_{1} \ $と$ \ \mathrm {Q}_{2} \ $に交互にオン信号とオフ信号を与える。図2の期間$ \ \mathrm {B} \ $は$ \ \fbox {　（１）　} \ $期間に相当する。

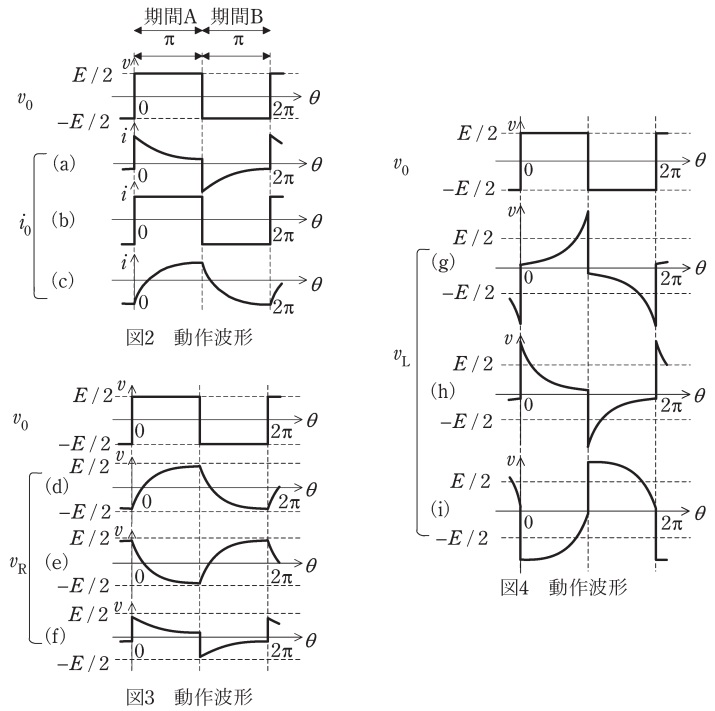
ここで負荷が誘導性の場合を考える。図2の交流電流$ \ i_{0} \ $の波形は，負荷の種類（抵抗，誘導性，容量性）に応じて流れる電流波形を順不同に示しているが，負荷が誘導性の場合に電圧$ \ v_{0} \ $に対して流れる電流$ \ i_{0} \ $としてとり得る波形は図2$ \ \fbox {　（２）　} \ $である。このときに，負荷の内で抵抗$ \ R \ $にかかる電圧$ \ v_{\mathrm {R}} \ $の波形は図3$ \ \fbox {　（３）　} \ $である。また，インダクタンス$ \ L \ $にかかる電圧$ \ v_{\mathrm {L}}=v_{\mathrm {0}}-v_{\mathrm {R}} \ $の波形は図4$ \ \fbox {　（４）　} \ $である。図2の電圧$ \ v_{0} \ $と図2$ \ \fbox {　（２）　} \ $の電流$ \ i_{0} \ $において，高調波成分を除いた基本波成分の電圧$ \ v_{\mathrm {f}} \ $と電流$ \ i_{\mathrm {f}} \ $の関係は，電圧$ \ v_{\mathrm {f}} \ $に対して$ \ \fbox {　（５）　} \ $の電流$ \ i_{\mathrm {f}} \ $が流れている。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　遅れ位相　　　　　　　&（ロ）&　進み位相　　　　　　　&（ハ）&　同位相 \\[ 5pt ] &（ニ）&　\left( \mathrm {a}\right)　　　　　&（ホ）&　\left( \mathrm {b}\right)　　　　　&（ヘ）&　\left( \mathrm {c}\right) \\[ 5pt ] &（ト）&　\left( \mathrm {d}\right)　　　　　&（チ）&　\left( \mathrm {e}\right)　　　　　&（リ）&　\mathrm {Q}_{2} \ にオン信号を与える \\[ 5pt ] &（ヌ）&　\left( \mathrm {f}\right)　　　　　&（ル）&　\left( \mathrm {g}\right)　　　　　&（ヲ）&　\mathrm {Q}_{1} \ にオン信号を与える \\[ 5pt ] &（ワ）&　\left( \mathrm {h}\right)　　　　　&（カ）&　\left( \mathrm {i}\right)　　　　　&（ヨ）&　\mathrm {Q}_{1} \ に負荷電流が流れる \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

ハーフブリッジ電圧形インバータの動作に関する問題です。
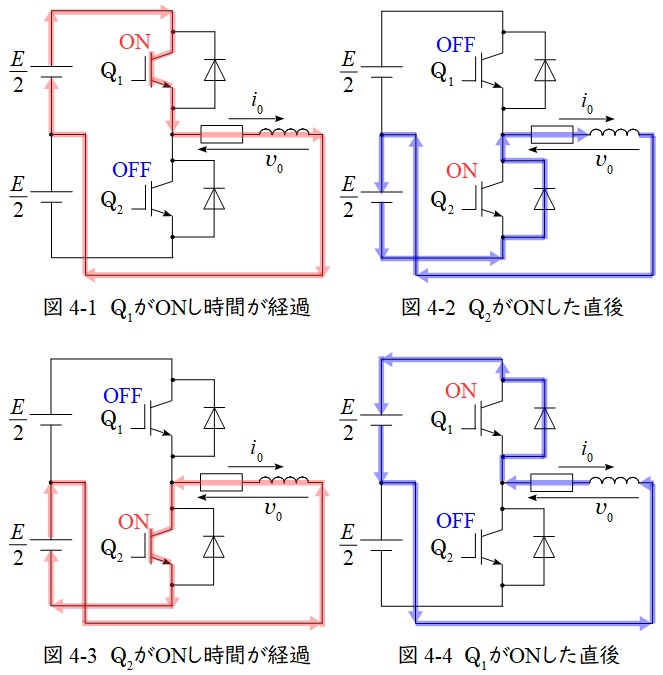
細かな名称を覚える必要はありませんが，パワーエレクトロニクスは図4-1～図4-4のような電流の変化をイメージできるかどうかが重要となります。
ハーフブリッジ電圧形インバータに限らず，あらゆる問題に適用できるようになりますので，理解しておくと良いかと思います。

1.ハーフブリッジ電圧形インバータの動作
ハーフブリッジ電圧形インバータの動作を図4-1～図4-4に示します。
図4-1の通り，$ \ \mathrm {Q}_{1} \ $がオン，$ \ \mathrm {Q}_{2} \ $がオフのとき，上側の電源$ \ \displaystyle \frac {E}{2} \ $から電力が供給され，リアクトルにエネルギーが蓄えられます。
次に，$ \ \mathrm {Q}_{1} \ $がオフ，$ \ \mathrm {Q}_{2} \ $がオンに切り替わると，図4-2のように切り替わった直後はリアクトルに蓄えられているエネルギーがあるため，リアクトルからエネルギーが放出され，下側の電源$ \ \displaystyle \frac {E}{2} \ $に電力が回生されます。
時間が十分に経過するとリアクトルのエネルギーがなくなるので，図4-3のように電流の流れが変わります。
さらに，$ \ \mathrm {Q}_{1} \ $がオン，$ \ \mathrm {Q}_{2} \ $がオフに切り替わると，図4-4のようにリアクトルからエネルギーが放出されリアクトルのエネルギーがなくなると図4-1のようになり，以後同じ動作を繰り返すようになります。

【解答】

(1)解答：リ
題意より解答候補は，（リ）$ \ \mathrm {Q}_{2} \ $にオン信号を与える，（ヲ）$ \ \mathrm {Q}_{1} \ $にオン信号を与える，（ヨ）$ \ \mathrm {Q}_{1} \ $に負荷電流が流れる，になると思います。
図2において期間$ \ \mathrm {B} \ $は$ \ v_{0}=-\displaystyle \frac {E}{2} \ $であるから，図4-2から図4-3までの期間となります。したがって，$ \ \mathrm {Q}_{2} \ $にオン信号を与える期間となります。

(2)解答：ヘ
題意より解答候補は，（ニ）$ \ \left( \mathrm {a}\right) \ $，（ホ）$ \ \left( \mathrm {b}\right) \ $，（ヘ）$ \ \left( \mathrm {c}\right) \ $，になると思います。
ワンポイント解説「1.ハーフブリッジ電圧形インバータの動作」の通り，電流$ \ i_{0} \ $は期間$ \ \mathrm {A} \ $に切り替わった直後は図4-4のように負の値であり，その後図4-1のように正の値になります。同様に$ \ \mathrm {B} \ $に切り替わった直後は図4-2のように正の値であり，その後図4-3のように負の値になります。
よって，正しい波形は$ \ \left( \mathrm {c}\right) \ $となります。

(3)解答：ト
題意より解答候補は，（ト）$ \ \left( \mathrm {d}\right) \ $，（チ）$ \ \left( \mathrm {e}\right) \ $，（ヌ）$ \ \left( \mathrm {f}\right) \ $，になると思います。
$ \ v_{\mathrm {R}}=Ri_{0} \ $であるため，波形は$ \ i_{0} \ $に比例します。よって，正しい波形は$ \ \left( \mathrm {d}\right) \ $となります。

(4)解答：ワ
題意より解答候補は，（ル）$ \ \left( \mathrm {g}\right) \ $，（ワ）$ \ \left( \mathrm {h}\right) \ $，（カ）$ \ \left( \mathrm {i}\right) \ $，になると思います。
$ \ v_{\mathrm {L}}=v_{\mathrm {0}}-v_{\mathrm {R}} \ $であるから，図3において$ \ v_{\mathrm {0}}-v_{\mathrm {R}} \ $を検討すると，波形は$ \ \left( \mathrm {h}\right) \ $となります。

(5)解答：イ
題意より解答候補は，（イ）遅れ位相，（ロ）進み位相，（ハ）同位相，になると思います。
ワンポイント解説「1.ハーフブリッジ電圧形インバータの動作」の通り，電圧が正負切り替わった後リアクトルのエネルギーが放出されてから電流の正負が切り替わるため，$ \ i_{\mathrm {f}} \ $は$ \ v_{\mathrm {f}} \ $に対して遅れ位相になっていると言えます。