《機械》〈情報伝送及び処理〉[R03:問8]アナログ信号からディジタル信号への変換に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，$ \ \mathrm {A} – \mathrm {D} \ $変換に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

アナログ信号をコンピュータで利用するには，$ \ \mathrm {A} – \mathrm {D} \ $変換によりディジタル信号に変換する必要がある。

連続したアナログ信号を適当な時間間隔で区切り，断続的な信号とすることを標本化という。標本化定理によると，入力信号を完全に復元するためには，その入力信号に含まれる最高周波数成分の$ \ \fbox {　（１）　} \ $倍を超えたサンプリングレートとすればよい。

標本化されたアナログ値を飛び飛びの不連続な数値で表すことを量子化という。量子化の段階数が増え，量子化の単位が小さくなるほど，量子化$ \ \fbox {　（２）　} \ $は小さくなる。

$ \ \mathrm {A} – \mathrm {D} \ $変換器には主に次のような方式がある。

積分形には，入力信号を一定時間積分し，この積分結果と一定の基準信号を積分した値が等しくなる$ \ \fbox {　（３）　} \ $を計測し，この計測値から変換結果を得る方式がある。サンプリングレートは低いが，高精度でノイズに強い方式である。

逐次比較形には，入力信号と内部の$ \ \mathrm {D} – \mathrm {A} \ $変換器の出力を$ \ 2 \ $分探索で比較していき，ディジタル値に変換する方式がある。$ \ \mathrm {n} \ $ビットの変換には，$ \ \fbox {　（４）　} \ $側から$ \ \mathrm {n} \ $回の比較が必要なため，中程度のサンプリングレートとなる。変換精度を得るために，$ \ \fbox {　（５）　} \ $回路により，標本化される信号レベルの変換終了まで変動しないようにする場合がある。

並列形はフラッシュ形とも称され，$ \ \mathrm {n} \ $ビットの変換には$ \ \left( 2^{\mathrm {n}}-1\right) \ $個の基準電圧と比較器を準備し，入力信号をそれらで同時に比較して変換する方式がある。高いサンプリングレートを得られるが，回路規模は大きくなる。

〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　10　　　　　&（ロ）&　0.5　　　　　&（ハ）&　オフセット \\[ 5pt ] &（ニ）&　\mathrm {LSB}　　　　　&（ホ）&　規模　　　　　&（ヘ）&　サンプルホールド \\[ 5pt ] &（ト）&　誤差　　　　　&（チ）&　2　　　　　&（リ）&　バンドパスフィルタ \\[ 5pt ] &（ヌ）&　\mathrm {MSB}　　　　　&（ル）&　位相　　　　　&（ヲ）&　アンチエイリアシング \\[ 5pt ] &（ワ）&　周期　　　　　&（カ）&　時間　　　　　　　&（ヨ）&　マスクビット \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

$ \ \mathrm {A ／ D} \ $変換に関する問題です。
電気工学というよりは無線工学の範囲の内容となるため，電験の対策としての優先順位は低いと考えて良いです。本問の内容は出題されても選択問題かと思います。

1.ディジタル伝送方式
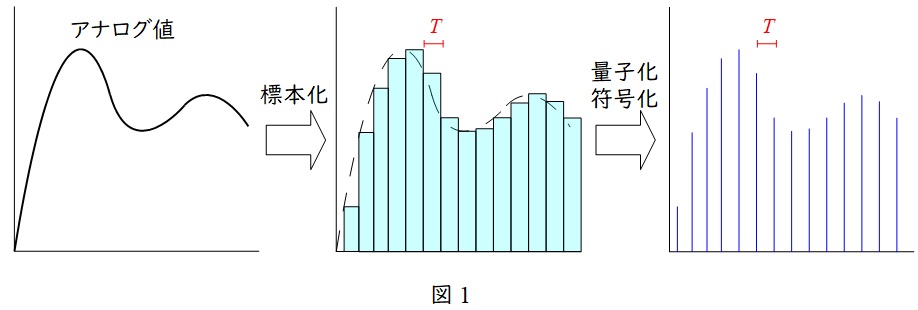
ディジタル伝送方式は，アナログ量である情報をデジタル量に変換($ \ \mathrm {A ／ D} \ $変換)してから情報を伝送する仕組みで，下記のような過程を経て情報を伝送します。

①標本化（サンプリング）
　アナログ量の大きさを一定周期$ \ T \ $ごとに読み取り，期間$ \ T \ $の間はその値が一定であるようにすることです。$ \ \displaystyle \frac {1}{T} \ $をサンプリング周波数と言います。サンプリング周波数の$ \ \displaystyle \frac {1}{2} \ $以上の周波数（ナイキスト周波数）を持つと，折り返し誤差が発生する(エイリアシング現象)ので，フィルタで除去する必要があります。

②量子化
　標本化した情報を$ \ \mathrm {A ／ D} \ $変換器でデジタル値に変換することを言います。

③符号化
　量子化した情報をサンプリング周波数毎のパルス化することを言います。

2.$ \ \mathrm {A ／ D} \ $変換の方式
①並列形（フラッシュ形）
$ \ \mathrm {n} \ $ビットの変換に$ \ \left( 2^{\mathrm {n}}-1\right) \ $個の基準電圧と比較器を準備し，入力信号をそれらで同時に比較して変換する方式です。
例えば，$ \ 0 \ \mathrm {V} \ $から$ \ 15 \ \mathrm {V} \ $を$ \ 1 \ \mathrm {V} \ $間隔で$ \ \mathrm {A ／ D} \ $変換する場合には，$ \ 1 \ \mathrm {V} \ $ずつの基準電圧と比較器を用意します。
方式が簡単で高いサンプリングレートを得られますが，比較器の数が増えるため回路規模は大きくなります。

②積分形
入力信号を一定時間積分し，その後入力信号と極性が逆の基準電圧を積分して零になるまでの時間を計測し，変換する方式です。
高精度でノイズに強い方式ですが，一定時間の積分が必要となるため高速化しにくい点があります。

③逐次比較型
入力信号を$ \ 1 \ $ビット毎に比較し，ディジタル値に変換していく方式です。
例えば，$ \ 11 \ \mathrm {V} \ $を$ \ 1 \ \mathrm {V} \ $間隔で$ \ 4 \ $桁のディジタル値にする場合，
・最上位の桁（$ \ \mathrm {MSB} \ $）である$ \ 8 \ \mathrm {V} \ $と比較し，大きいので$ \ 1 \ $に変換
・２番目の桁である$ \ 4 \ \mathrm {V} \ $と比較して，$ \ 12 \ \mathrm {V} \ $より小さいので$ \ 0 \ $に変換
・３番目の桁である$ \ 2 \ \mathrm {V} \ $と比較して，$ \ 10 \ \mathrm {V} \ $より大きいので$ \ 1 \ $に変換
・最下位の桁である$ \ 1 \ \mathrm {V} \ $と比較して，$ \ 11 \ \mathrm {V} \ $と等しいので$ \ 1 \ $に変換
というような過程を経て$ \ 1011 \ $と変換するような方式です。
$ \ \mathrm {n} \ $ビットへの変換に$ \ \mathrm {n} \ $回の比較が必要なため，中程度のサンプリングレートとなります。
変換精度を得るために，変換完了までの間入力信号が変動しない様に保持（サンプルホールド）する場合が多いです。

【解答】

(1)解答：チ
題意より，解答候補は（イ）$ \ 10 \ $，（ロ）$ \ 0.5 \ $，（チ）$ \ 2 \ $，になると思います。
ワンポイント解説「1.ディジタル伝送方式」でも触れていますが，標本化定理は最高周波数成分の$ \ 2 \ $倍を超えたサンプリングレートとすれば元の信号波形に復元することができるという定理です。

(2)解答：ト
題意より，解答候補は（ハ）オフセット，（ホ）規模，（ト）誤差，（ル）位相，（ワ）周期，（カ）時間，等になると思います。
この空欄は感覚的にわかるかと思いますが，量子化の単位を小さくすればするほど，アナログ値に近い値となり誤差は小さくなります。（例えば$ \ 1 \ \mathrm {V} \ $単位から$ \ 0.1 \ \mathrm {V} \ $単位にすると誤差は減ることがわかると思います）

(3)解答：カ
題意より，解答候補は（ホ）規模，（ル）位相，（ワ）周期，（カ）時間，等になると思います。
ワンポイント解説「2.$ \ \mathrm {A ／ D} \ $変換の方式」の通り，積分形において変換するための重要なファクターは時間となります。

(4)解答：ヌ
題意より，解答候補は（ニ）$ \ \mathrm {LSB} \ $，（ヌ）$ \ \mathrm {MSB} \ $，等になると思います。
ワンポイント解説「2.$ \ \mathrm {A ／ D} \ $変換の方式」の通り，逐次変化形の変換は最上位のビット（$ \ \mathrm {MSB} \ $）側から比較していきます。

(5)解答：ヘ
題意より，解答候補は（ハ）オフセット，（ヘ）サンプルホールド，（リ）バンドパスフィルタ，（ヲ）アンチエイリアシング，（ヨ）マスクビット，等になると思います。
ワンポイント解説「2.$ \ \mathrm {A ／ D} \ $変換の方式」の通り，逐次変化形において，標本化される信号レベルが変換終了まで変動しない様にする回路をサンプルホールド回路といいます。