Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,三相同期発電機の並行運転に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
仕様及び特性が等しい\( \ 2 \ \)台の三相同期発電機\( \ \mathrm {SG1} \ \)及び\( \ \mathrm {SG2} \ \)を並列接続し,共通の負荷に電力を供給することを考える。速度出力特性がともに等しい垂下特性をもつ原動機で入力を等しく一定として並行運転している場合,両機の間には横流と呼ばれる循環電流は流れない。このとき,各発電機の誘導起電力の大きさ,周波数が等しく,各発電機の誘導起電力の\( \ \fbox { (1) } \ \)がほぼ一致している。この運転状態から\( \ \mathrm {SG1} \ \)の界磁電流を\( \ \fbox { (2) } \ \)すると,両機の誘導起電力に差が生じ,これによって両機の間に循環電流が流れる。この電流は\( \ \mathrm {SG1} \ \)の誘導起電力に対しては遅れ,\( \ \mathrm {SG2} \ \)に対しては進みの\( \ \fbox { (3) } \ \)電流であり,電機子反作用によってそれぞれの磁束に作用して,両機の端子電圧が界磁電流の調整前と比べて\( \ \fbox { (4) } \ \)電圧で平衡を保つように働く。
また,先の並行運転状態において,何らかの原因で一方の発電機の回転速度が一時的に変化し,両機の速度差により誘導起電力の間にわずかな位相差が生じて循環電流が流れたとする。この場合の循環電流は,両機の間で有効電力の授受を行って自動的に両機を同一位相に保つように働く。この場合の循環電流を\( \ \fbox { (5) } \ \)電流という。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& 消費 &(ロ)& 増加 &(ハ)& 有効 \\[ 5pt ]
&(ニ)& 減少 &(ホ)& 無効 &(ヘ)& 力率角 \\[ 5pt ]
&(ト)& 高い &(チ)& 負荷角 &(リ)& 低い \\[ 5pt ]
&(ヌ)& 制限 &(ル)& 同じ &(ヲ)& 位相 \\[ 5pt ]
&(ワ)& 制御 &(カ)& 同期化 &(ヨ)& 共振 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
同期発電機の並行運転に関する問題です。
「2.同期発電機の無効循環電流(無効横流),同期化電流」の内容は\( \ 1 \ \)種レベルの内容となりますので,一先ずは暗記でも構いませんが,各名称や位相と大きさのどちらが有効電流と無効電流に関係しているのか等は整理しておくようにしましょう。
1.同期発電機の並列条件
同期発電機の並列条件と調整方法は以下の5つです。電圧,周波数,位相の一致が必須であることを覚えておきましょう。
①電圧の大きさが等しいこと → 励磁電流を調整する。
②周波数が等しいこと → 原動機の回転数を調整する。
③位相が等しいこと → 同期検定器を使用し,位相が合った所で並列する。
④電圧の波形が等しいこと → 回転子の回転速度を一定にする。
⑤相回転が等しいこと → 発電機点検後に相回転方向を確認しておく。
2.同期発電機の無効循環電流(無効横流),同期化電流
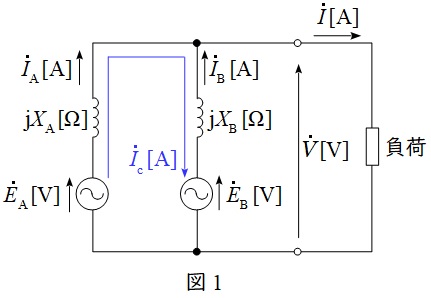
同期発電機の並行運転時の一相分等価回路は電機子巻線抵抗を無視すると図1のようになり,回路方程式は,
\[
\begin{eqnarray}
\dot I &=& {\dot I}_{\mathrm {A}}+{\dot I}_{\mathrm {B}} & ・・・・・・・・・・・・・・・・・ ①& \\[ 5pt ]
\dot V &=& {\dot E}_{\mathrm {A}}-\mathrm {j}X_{\mathrm {A}}{\dot I}_{\mathrm {A}} & ・・・・・・・・・・・・・・・・・ ②& \\[ 5pt ]
\dot V &=& {\dot E}_{\mathrm {B}}-\mathrm {j}X_{\mathrm {B}}{\dot I}_{\mathrm {B}} & ・・・・・・・・・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
となるので,②式及び③式より,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {A}}-\mathrm {j}X{\dot I}_{\mathrm {A}} &=& {\dot E}_{\mathrm {B}}-\mathrm {j}X_{\mathrm {B}}{\dot I}_{\mathrm {B}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,①式を代入して\( \ {\dot I}_{\mathrm {B}} \ \)を消去すると,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {A}}-\mathrm {j}X_{\mathrm {A}}{\dot I}_{\mathrm {A}} &=& {\dot E}_{\mathrm {B}}-\mathrm {j}X_{\mathrm {B}}\left( \dot I -{\dot I}_{\mathrm {A}}\right) \\[ 5pt ]
{\dot E}_{\mathrm {A}}-\mathrm {j}X_{\mathrm {A}}{\dot I}_{\mathrm {A}} &=& {\dot E}_{\mathrm {B}}-\mathrm {j}X_{\mathrm {B}}\dot I +\mathrm {j}X_{\mathrm {B}}{\dot I}_{\mathrm {A}} \\[ 5pt ]
\mathrm {j}\left( X_{\mathrm {A}}+X_{\mathrm {B}}\right) {\dot I}_{\mathrm {A}} &=& {\dot E}_{\mathrm {A}}-{\dot E}_{\mathrm {B}}+\mathrm {j}X_{\mathrm {B}}\dot I \\[ 5pt ]
{\dot I}_{\mathrm {A}} &=& \frac {X_{\mathrm {B}}}{X_{\mathrm {A}}+X_{\mathrm {B}}}\dot I+\frac {{\dot E}_{\mathrm {A}}-{\dot E}_{\mathrm {B}}}{\mathrm {j}\left( X_{\mathrm {A}}+X_{\mathrm {B}}\right) } \\[ 5pt ]
&=& \frac {X_{\mathrm {B}}}{X_{\mathrm {A}}+X_{\mathrm {B}}}\dot I-\mathrm {j}\frac {{\dot E}_{\mathrm {A}}-{\dot E}_{\mathrm {B}}}{X_{\mathrm {A}}+X_{\mathrm {B}}} ・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {B}}&=&\dot I – {\dot I}_{\mathrm {A}} \\[ 5pt ]
&=& \frac {X_{\mathrm {A}}}{X_{\mathrm {A}}+X_{\mathrm {B}}}\dot I+\mathrm {j}\frac {{\dot E}_{\mathrm {A}}-{\dot E}_{\mathrm {B}}}{X_{\mathrm {A}}+X_{\mathrm {B}}} \ \ ・・・・・・・・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
となります。また,端子電圧\( \ \dot V \ \)は,②式に④式を代入すると,
\[
\begin{eqnarray}
\dot V &=& {\dot E}_{\mathrm {A}}-\mathrm {j}X_{\mathrm {A}}\left( \frac {X_{\mathrm {B}}}{X_{\mathrm {A}}+X_{\mathrm {B}}}\dot I-\mathrm {j}\frac {{\dot E}_{\mathrm {A}}-{\dot E}_{\mathrm {B}}}{X_{\mathrm {A}}+X_{\mathrm {B}}}\right) \\[ 5pt ]
&=& \frac {\left( X_{\mathrm {A}}+X_{\mathrm {B}}\right) {\dot E}_{\mathrm {A}} }{X_{\mathrm {A}}+X_{\mathrm {B}}}-\frac {X_{\mathrm {A}}\left( {\dot E}_{\mathrm {A}}-{\dot E}_{\mathrm {B}}\right) }{X_{\mathrm {A}}+X_{\mathrm {B}}}-\mathrm {j}\frac {X_{\mathrm {A}}X_{\mathrm {B}}}{X_{\mathrm {A}}+X_{\mathrm {B}}}\dot I \\[ 5pt ]
&=& \frac {X_{\mathrm {A}}{\dot E}_{\mathrm {B}}+X_{\mathrm {B}}{\dot E}_{\mathrm {A}}}{X_{\mathrm {A}}+X_{\mathrm {B}}}-\mathrm {j}\frac {X_{\mathrm {A}}X_{\mathrm {B}}}{X_{\mathrm {A}}+X_{\mathrm {B}}}\dot I ・・・・・・・・・・ ⑥ \\[ 5pt ]
\end{eqnarray}
\]
となります。さらに,④式,⑤式を比較すると循環電流\( \ {\dot I}_{\mathrm {c}} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {c}}&=&-\mathrm {j}\frac {{\dot E}_{\mathrm {A}}-{\dot E}_{\mathrm {B}}}{X_{\mathrm {A}}+X_{\mathrm {B}}}= \frac {{\dot E}_{\mathrm {A}}-{\dot E}_{\mathrm {B}}}{\mathrm {j}\left( X_{\mathrm {A}}+X_{\mathrm {B}}\right) } \\[ 5pt ]
\end{eqnarray}
\]
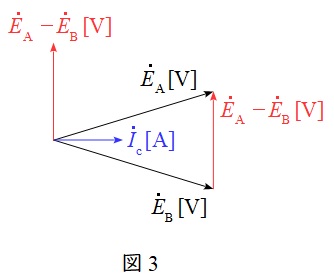
と求められます。上式より,循環電流\( \ {\dot I}_{\mathrm {c}} \ \)は\( \ {\dot E}_{\mathrm {A}} \ \)と\( \ {\dot E}_{\mathrm {B}} \ \)の位相が等しく大きさが異なる時には,無効循環電流(無効横流)が流れ,\( \ {\dot E}_{\mathrm {A}} \ \)と\( \ {\dot E}_{\mathrm {B}} \ \)の大きさが等しく位相が異なる時には,有効電流(同期化電流)が流れることが分かります。
これをベクトル図で表すと図2及び図3となります。

【解答】
(1)解答:ヲ
題意より解答候補は,(ヘ)力率角,(チ)負荷角,(ヲ)位相,になると思います。
ワンポイント解説「1.同期発電機の並列条件」の通り,並列運転の条件として位相の一致があります。
(2)解答:ロ
題意より解答候補は,(ロ)増加,(ニ)減少,(ヌ)制限,になると思います。
ワンポイント解説「2.同期発電機の無効循環電流(無効横流),同期化電流」の通り,図1及び図2の例で行くと,電圧の高い\( \ {\dot E}_{\mathrm {A}} \ \)から見ると\( \ {\dot I}_{\mathrm {c}} \ \)の遅れ無効電流,電圧の低い\( \ {\dot E}_{\mathrm {B}} \ \)から見ると\( \ -{\dot I}_{\mathrm {c}} \ \)の進み無効電流が流れることが分かります。したがって,\( \ \mathrm {SG1} \ \)の界磁電流を増加すると\( \ \mathrm {SG1} \ \)の誘導起電力が増加するので,\( \ \mathrm {SG1} \ \)の誘導起電力に対しては遅れ,\( \ \mathrm {SG2} \ \)に対しては進みの無効電流が流れます。
(3)解答:ホ
題意より解答候補は,(ハ)有効,(ホ)無効,等になると思います。
ワンポイント解説「2.同期発電機の無効循環電流(無効横流),同期化電流」の通り,誘導起電力の大きさの違いによる電流は無効電流となります。
(4)解答:ト
題意より解答候補は,(ト)高い,(リ)低い,(ル)同じ,になると思います。
\( \ \mathrm {SG1} \ \)の誘導起電力が増加するので,\( \ \mathrm {SG1} \ \)の誘導起電力に対しては遅れ,\( \ \mathrm {SG2} \ \)に対しては進みの無効電流が流れるので,\( \ \mathrm {SG1} \ \)は減磁作用,\( \ \mathrm {SG2} \ \)は増磁作用の電機子反作用が働き,本問の例においては全体としては\( \ \mathrm {SG2} \ \)の電圧が上昇した分,両機の端子電圧は高い電圧で平衡を保つようになります。
(5)解答:カ
題意より解答候補は,(イ)消費,(ハ)有効,(ヌ)制限,(ワ)制御,(カ)同期化,等になると思います。
ワンポイント解説「2.同期発電機の無効循環電流(無効横流),同期化電流」の通り,両機の誘導起電力の間にわずかな位相差が生じて循環電流が流れたときの電流を同期化電流といいます。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは