《機械》〈電熱〉[R05:問6]赤外加熱の原理や法則に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，赤外加熱に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

赤外加熱は赤外放射による伝熱を主体にした加熱方式である。赤外放射は可視放射との境界（$ \ \fbox {　（１）　} \ $）を短波長端とし，電波との境界（波長$ \ 1 \ \mathrm {mm} \ $）を長波長端とする波長範囲の電磁波の総称である。ただし，実際の赤外加熱において考慮すべき赤外放射の長波長端はせいぜい$ \ 15 \ \mathrm {\mu m} \ $である。

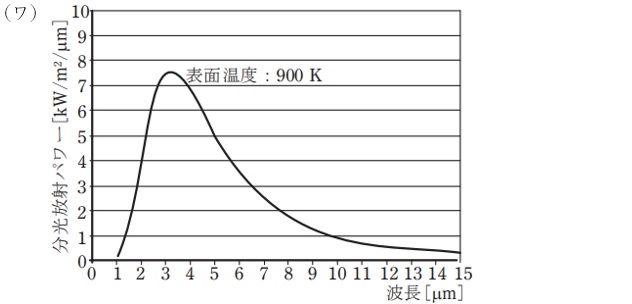
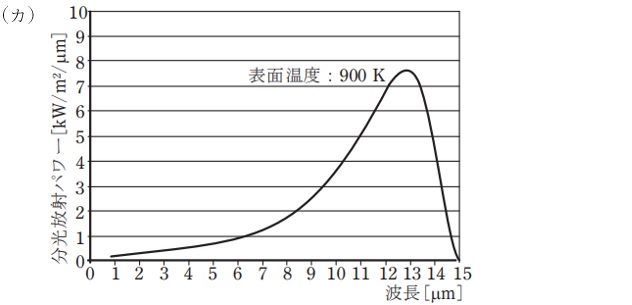
赤外加熱に用いられる赤外放射源は，電熱線によって加熱されたセラミックスや，通電によって高温になったフィラメントなどである。放射源表面の単位面積から放射される分光放射パワーは，表面の分光放射率とプランクの放射則で規定される黒体の分光放射パワーとの積によって表すことができる。なお，黒体の分光放射パワーの特性は，例えば黒体表面の温度が$ \ 900 \ \mathrm {K} \ $の場合，グラフ$ \ \fbox {　（２）　} \ $のようになる。

また，黒体の全放射パワーは絶対温度の$ \ 4 \ $乗に比例する。これは$ \ \fbox {　（３）　} \ $と呼ばれている。また，分光放射パワーが最大となる波長は黒体表面の絶対温度$ \ \fbox {　（４）　} \ $する。これはウィーンの変位則と呼ばれている。

赤外加熱の加熱対象には，プラスチックや塗料などの有機物質や食品などが多い。これらの物質は赤外放射の波長領域において多くの吸収帯をもつ。これらの表面に照射された赤外放射は，内部に浸透する過程で吸収されて熱に変わり，物質自体が発熱する。一般に，赤外加熱の加熱対象は赤外放射をよく吸収するがゆえに，赤外放射の浸透深さはせいぜい$ \ \fbox {　（５）　} \ $のオーダーである。この領域で発生した熱は，その後，伝導や対流によって内部に伝わり，加熱が進む。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　と無関係に変化　　　　　　&（ロ）&　波長 \ 0.68 \ \mathrm {\mu m}　　　　　&（ハ）&　波長 \ 0.78 \ \mathrm {\mu m} \\[ 5pt ] &（ニ）&　ヴィーデマン・フランツの法則　　　　　　　　　　&（ホ）&　波長 \ 0.88 \ \mathrm {\mu m}　　　　　&（ヘ）&　1～10 \ \mathrm {mm} \\[ 5pt ] &（ト）&　レイリー・ジーンズの法則　　　　　&（チ）&　0.1～1 \ \mathrm {mm}　　　　　&（リ）&　10～100 \ \mathrm {\mu m} \\[ 5pt ] &（ヌ）&　ステファン・ボルツマンの法則　　　　　&（ル）&　に比例　　　　　&（ヲ）&　に反比例 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

赤外加熱の原理や各種法則に関する問題です。
近年あまり出題されてこなかった内容なので，受験生にとっては厳しい問題であったかなと思います。
出題されている内容はいずれも赤外加熱の分野では重要な内容ばかりですので，覚えておくようにしましょう。

1.赤外加熱
可視光との境界である波長$ \ 0.78 \ \mathrm {\mu m} \ $以上の赤外線による熱放射を利用して，加熱物を加熱する方法です。物質表面から放射される全放射パワーが絶対温度で表した表面温度の$ \ 4 \ $乗に比例するというステファン・ボルツマンの法則に従って加熱されます。
塗装や印刷の乾燥のほか，食品，電子部品，半導体，プラスチックなどの製造工程においても用いられています。

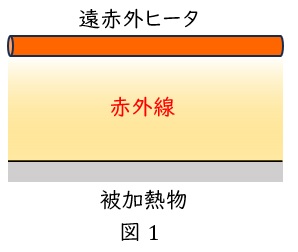
2.ステファン・ボルツマンの法則
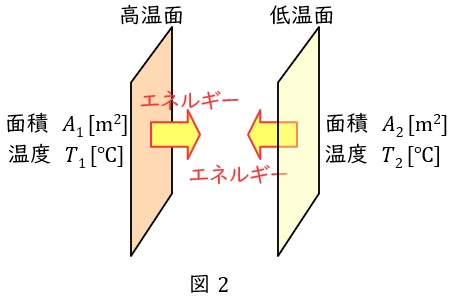
図2のように，面積$ \ A_{1} \ \mathrm {[m^{2}]} \ $，温度$ \ T_{1} \ \mathrm {[K]} \ $の高温面と，面積$ \ A_{2} \ \mathrm {[m^{2}]} \ $，温度$ \ T_{2} \ \mathrm {[K]} \ $の低温面があるとき，$ \ 1 \ $秒当たりに高温面から低温面に伝わるエネルギー$ \ \mathit {\Phi } \ \mathrm {[W]} \ $は，$ \ \varepsilon \ $を放射率，$ \ \sigma \ \mathrm {[W / \left( m^{2}\cdot K^{4}\right) ]} \ $をステファン・ボルツマン定数，$ \ F_{12} \ $を形態係数とすると，
\[
\begin{eqnarray}
\mathit {\Phi } &=& \varepsilon \sigma A_{1}F_{12}\left( T_{1}^{4}-T_{2}^{4}\right) \\[ 5pt ] \end{eqnarray}
\] で求められるという法則です。

3.ウィーンの変位則
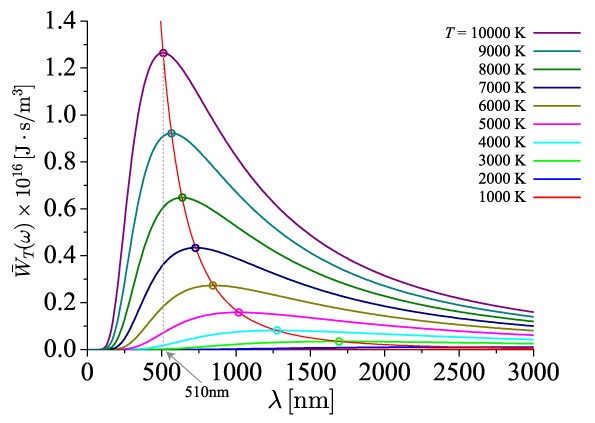
黒体から放射されるエネルギーは黒体の温度によってその大きさが変わり，その波長特性はプランクの法則に従い下図のようになります。
このとき物体表面から放射される放射パワーがピークとなる波長$ \ \lambda _{\mathrm {m}} \ \mathrm {[\mu m]} \ $は温度$ \ T \ \mathrm {[K]} \ $に反比例し，
\[
\begin{eqnarray}
\lambda _{\mathrm {m}} &≒& \frac {2898}{T} \\[ 5pt ] \end{eqnarray}
\] となる関係があり，これをウィーンの変位則といいます。

出典：natural science ホームページ
https://www.natural-science.or.jp/article/20111230191657.php

【解答】

(1)解答：ハ
題意より解答候補は，（ロ）波長$ \ 0.68 \ \mathrm {\mu m} \ $，（ハ）波長$ \ 0.78 \ \mathrm {\mu m} \ $，（ホ）波長$ \ 0.88 \ \mathrm {\mu m} \ $，になると思います。
ワンポイント解説「1.赤外加熱」の通り，赤外放射は可視光との境界である波長$ \ 0.78 \ \mathrm {\mu m} \ $を短波長端とした電磁波の総称です。

(2)解答：ワ
題意より解答候補は，（ワ），（カ），（ヨ），のグラフになると思います。
ワンポイント解説「3.ウィーンの変位則」の通り，黒体表面の温度が$ \ 900 \ \mathrm {K} \ $の場合の分光放射パワーの特性は（ワ）のグラフのようになります。

(3)解答：ヌ
題意より解答候補は，（ニ）ヴィーデマン・フランツの法則，（ト）レイリー・ジーンズの法則，（ヌ）ステファン・ボルツマンの法則，になると思います。
ワンポイント解説「2.ステファン・ボルツマンの法則」の通り，黒体の全放射パワーは絶対温度の$ \ 4 \ $乗に比例するという法則はステファン・ボルツマンの法則といいます。ヴィーデマン・フランツの法則やレイリー・ジーンズの法則も熱伝導や熱放射に関連する法則ですが，電験では今のところ出題されたのを見たことはありません。

(4)解答：ヲ
題意より解答候補は，（イ）と無関係に変化，（ル）に比例，（ヲ）に反比例，になると思います。
ワンポイント解説「3.ウィーンの変位則」の通り，分光放射パワーが最大となる波長は黒体表面の絶対温度に反比例します。

(5)解答：リ
題意より解答候補は（ヘ）$ \ 1～10 \ \mathrm {mm} \ $，（チ）$ \ 0.1～1 \ \mathrm {mm} \ $，（リ）$ \ 10～100 \ \mathrm {\mu m} \ $，になると思います。
赤外放射における浸透深さはその波長が短ければ短いほど深くなりますが，一般にその浸透深さは$ \ 10～100 \ \mathrm {\mu m} \ $程度となります。