《機械》〈電熱〉[R06:問7]誘導加熱の原理と特徴に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，誘導加熱に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

誘導加熱は，金属の溶解，鍛造，圧延などのほか，焼き入れなどの金属表面処理にも用いられている。

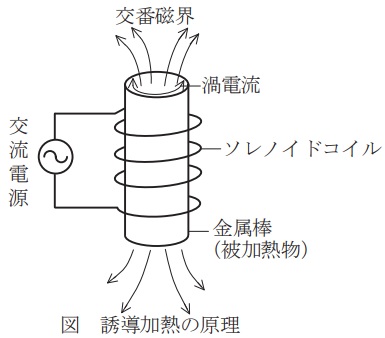
図は誘導加熱の原理を示すためのものである。交流電源に接続したソレノイドコイルの中には，被加熱物である円柱状の金属棒が挿入されている。コイルによって発生する交番磁界は金属棒を貫通し，電磁誘導によって金属棒に渦電流が流れる。この渦電流によるジュール熱によって金属棒が加熱される。金属棒が鉄系金属などの強磁性体の場合には，\( \ \fbox {　 （１） 　} \ \)による発熱も加熱に寄与する。

渦電流は金属棒の表面側に集まる性質がある。この性質は\( \ \fbox {　 （２） 　} \ \)と呼ばれ，これを表す指標として\( \ \fbox {　 （３） 　} \ \delta \ \mathrm {[m]} \ \)が用いられている。\( \ \delta \ \)は次式で与えられる。
\[
\begin{eqnarray}
\delta &=& \sqrt {\frac {\rho }{\pi f \mu _{\mathrm {r}}\mu _{0}}} \ \mathrm {[m]}　 \ ・・・・・・・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] ただし, \( \ \ f \ \ \)：交流電源の周波数\( \ \mathrm {[Hz]} \ \)
　　　　\( \ \rho \ \ \)：金属棒の抵抗率\( \ \mathrm {[\Omega \cdot m]} \ \)
　　　　\(\mu _{\mathrm {r}} \ \)：金属棒の比透磁率\( \ [ – ] \ \)
　　　　\(\mu _{\mathrm {0}} \ \)：真空の透磁率\( \ \left( 1.257\times 10^{-6} \ \mathrm {[H / m]} \right) \ \)
ここで，誘導加熱の様相の概要を理解するために，\( \ \delta \ \)は金属棒の半径\( \ a \ \mathrm {[m]} \ \)よりも十分小さいものとし，また，加熱が進んで金属棒内の温度分布が一様でなくなっても，\( \ \rho \ \)，\( \ \mu _{\mathrm {r}} \ \)の値の分布に変化はなく，一定，一様のままであると仮定すると，金属棒の側面表面から深さ\( \ x \ \mathrm {[m]} \ \)における電流密度\( \ i \left( x\right) \ \mathrm {[A / m^{2}]} \ \)は次式で与えられる。
\[
\begin{eqnarray}
i \left( x\right) &=& i_{0}\mathrm {e}^{-\frac {x}{\delta }} \ \mathrm {[A / m^{2}]}　 ・・・・・・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] ただし，\( \ i_{0} \ \)：金属棒の側面表面\( \ \left( x=0\right) \ \)における電流密度\( \ \mathrm {[A / m^{2}]} \ \)

②式から，金属棒に流れる単位長さあたりの電流のうち，金属棒の側面表面から深さ\( \ \delta \ \)までの区間を流れる電流\( \ I_{0\sim \delta } \ \mathrm {[A / m]} \ \)は以下のようになる。
\[
\begin{eqnarray}
I_{0\sim \delta } &=& \int _{0}^{\delta } i \left( x\right) \mathrm {d}x=\int _{0}^{\delta } i_{0}\mathrm {e}^{-\frac {x}{\delta }}\mathrm {d}x=\left[ -i_{0}\delta \mathrm {e}^{-\frac {x}{\delta }}\right] _{0}^{\delta }=i_{0}\delta \left( 1-\frac {1}{\mathrm {e}}\right) ≈0.632i_{0}\delta 　・・・　③ \\[ 5pt ] \end{eqnarray}
\] ただし，\( \ \mathrm {e}= 2.718 \ 28 \ \)

さらに，③式において\( \ \delta ≪ a \ \)であることを考慮すると，金属棒に流れる単位長さあたりの全電流\( \ I \ \mathrm {[A / m]} \ \)は以下のようになる。
\[
\begin{eqnarray}
I &≈& \ \fbox {　 （４） 　} \ ・・・・・・・・・・・・・・・・・・・・・　④ \\[ 5pt ] \end{eqnarray}
\] ①式において，\( \ \delta \ \)は\( \ f \ \)だけでなく，\( \ \rho \ \)，\( \ \mu _{\mathrm {r}} \ \)にも依存する。実際の誘導加熱においては，\( \ \rho \ \)，\( \ \mu _{\mathrm {r}} \ \)は温度によって変化する。さらに，金属棒が鉄系金属などの強磁性体の場合，ある温度\( \ ( \ \fbox {　 （５） 　} \ ) \ \)まで上昇すると，性質が強磁性から常磁性に変化し，\( \ \mu _{\mathrm {r}} \ \)が急激に低下する。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　磁気ひずみ　　　　　　　&（ロ）&　磁気ヒステリシス　　　　　　　&（ハ）&　磁気制動 \\[ 5pt ] &（ニ）&　浸透深さ　　　　　&（ホ）&　キュリー点　　　　　&（ヘ）&　浸潤深度 \\[ 5pt ] &（ト）&　近接効果　　　　　&（チ）&　ゼーベック効果　　　　　&（リ）&　表皮効果 \\[ 5pt ] &（ヌ）&　深達度　　　　　&（ル）&　回帰不能点　　　　　&（ヲ）&　特異点 \\[ 5pt ] &（ワ）&　i_{0}\delta　　　　　&（カ）&　i_{0}a　　　　　&（ヨ）&　\frac {i_{0}a}{2} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

誘導加熱の原理と特徴を問う問題です。
前半の(3)までが正答しておきたい内容，\( \ 2 \ \)種二次試験合格を目指すのであれば(4)の読解からの計算も解けるようにしておきたい内容です。
近年は選択問題が多いですが，電熱の分野は\( \ 3 \ \)種に比べ出題割合が高い印象ですので，参考書等でよく対策しておくようにしましょう。

1.誘導加熱
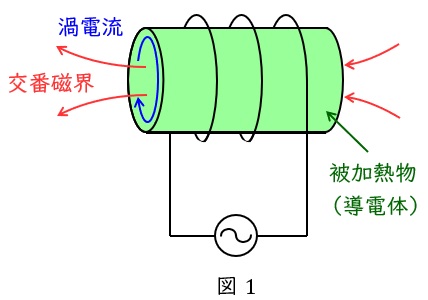
交番磁界中に導電体を置くことによって，ファラデーの電磁誘導の法則により渦電流が生じ，その抵抗損（ジュール損）によって発熱します。オール電化のコンロ等はこの原理を利用しています。
交番磁束は表皮効果によって被加熱物の表面近くに集まり，渦電流も被加熱物の表面付近に集中します。その指標として誘導加熱による物体への電流浸透の深さ\( \ \delta \ \mathrm {[cm]} \ \)があり，比透磁率\( \ \mu _{\mathrm {s}} \ \)，抵抗率\( \ \rho \ \mathrm {[\mu \Omega \cdot cm]} \ \)，周波数\( \ f \ \mathrm {[Hz]} \ \)とすると，
\[
\begin{eqnarray}
\delta &≃&5.03\sqrt {\frac {\rho }{\mu _{\mathrm {s}} f}} \\[ 5pt ] \end{eqnarray}
\] となり，周波数が低いほど物体への電流浸透の深さは深くなります。

【解答】

(1)解答：ロ
題意より解答候補は，（イ）磁気ひずみ，（ロ）磁気ヒステリシス，（ハ）磁気制動，等になると思います。
強磁性体に発生する損失（発熱）は磁気ヒステリシスによる発熱となります。ヒステリシス損はヒステリシスループに囲まれた面積に比例した値となり，理論科目で学習する内容ですので，忘れてしまった方は復習しておくようにして下さい。

(2)解答：リ
題意より解答候補は，（ト）近接効果，（チ）ゼーベック効果，（リ）表皮効果，になると思います。
ワンポイント解説「1.誘導加熱」の通り，渦電流が金属棒の表面側に集まる性質を表皮効果といいます。近接効果は電線同士が近いことで電流の偏りが生じる現象，ゼーベック効果は異なる金属で閉回路を作り接続点に温度差を設けると起電力が生じる現象です。

(3)解答：ニ
題意より解答候補は，（ニ）浸透深さ，（ヘ）浸潤深度，（ヌ）深達度，等になると思います。
ワンポイント解説「1.誘導加熱」の通り，表皮効果を表す指標として用いられるのは浸透深さ\( \ \delta \ \mathrm {[m]} \ \)となります。

(4)解答：ワ
③式において，\( \ \delta ≪ a \ \)であるとしたときの金属棒に流れる単位長さあたりの全電流\( \ I \ \mathrm {[A / m]} \ \)は，
\[
\begin{eqnarray}
I&=& \int _{0}^{a} i \left( x\right) \mathrm {d}x \\[ 5pt ] &=&\int _{0}^{a} i_{0}\mathrm {e}^{-\frac {x}{\delta }}\mathrm {d}x \\[ 5pt ] &=&\left[ -i_{0}\delta \mathrm {e}^{-\frac {x}{\delta }}\right] _{0}^{a} \\[ 5pt ] &=&i_{0}\delta \left( 1- \mathrm {e}^{-\frac {a}{\delta }}\right) \\[ 5pt ] &≈&i_{0}\delta \left( 1- 0\right) \\[ 5pt ] &=&i_{0}\delta \\[ 5pt ] \end{eqnarray}
\] と求められます。

(5)解答：ホ
題意より解答候補は，（ホ）キュリー点，（ル）回帰不能点，（ヲ）特異点，になると思います。
強磁性体の場合，ある一定以上の温度まで上昇すると磁化が小さくなり強磁性から常磁性に変化する性質があり，その温度をキュリー点といいます。キュリー点は材料により異なります。