Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,三相誘導電動機に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
三相誘導電動機の滑りは負荷によって変化し,トルクは滑りの関数として表される。
星形一相分の等価回路において,一次電圧を\( \ V_{1} \ \mathrm {[V]} \ \),滑りを\( \ s \ \),一次回路の抵抗と漏れリアクタンスをそれぞれ\( \ r_{1} \ \mathrm {[\Omega ]} \ \)及び\( \ x_{1} \ \mathrm {[\Omega ]} \ \),一次側に換算した二次回路の抵抗と漏れリアクタンスをそれぞれ\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)及び\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \),同期角速度を\( \ \omega _{0} \ \mathrm {[rad / s]} \ \)とすれば,トルク\( \ T \ \mathrm {[N\cdot m]} \ \)は次式で表される。
\[
\begin{eqnarray}
T &=& \frac {1}{\omega _{0}}\cdot \frac {\displaystyle \ \fbox { (1) } \ \times \frac {r_{2}^{\prime }}{s}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \ \mathrm {[N\cdot m]} \\[ 5pt ]
\end{eqnarray}
\]
このように,トルク\( \ T \ \)は滑り\( \ s \ \)の関数であるから,\( \ \displaystyle \frac {\mathrm {d}T}{\mathrm {d}s}=0 \ \)とすると極値となり,このときの滑り\( \ s_{\mathrm {t}} \ \)を,
\[
\begin{eqnarray}
s_{\mathrm {t}} &=& ±\frac {r_{2}^{\prime }}{\sqrt {r_{1}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
として求めることができる。電動機運転では\( \ \fbox { (2) } \ \)であるから符号は\( \ + \ \)となる。この結果から,最大トルクを求めることができる。最大トルクは\( \ \fbox { (3) } \ \)トルクと呼ばれ,\( \ \fbox { (4) } \ \)に関係なく一定である。
誘導電動機のトルク-速度特性において,同期速度に近い範囲では,トルク\( \ T \ \)は滑り\( \ s \ \)にほぼ\( \ \fbox { (5) } \ \)。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& r_{1} &(ロ)& s=1 &(ハ)& 3V_{1}^{2} \\[ 5pt ]
&(ニ)& 同期 &(ホ)& 脱出 &(ヘ)& V_{1}^{2} \\[ 5pt ]
&(ト)& s < 0 &(チ)& r_{2}^{\prime } &(リ)& 無関係である \\[ 5pt ]
&(ヌ)& s > 0 &(ル)& 停動 &(ヲ)& 3V_{1}^{2}\left( 1-s \right) \\[ 5pt ]
&(ワ)& 比例する &(カ)& x_{2}^{\prime } &(ヨ)& 反比例する \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
三相誘導電動機のトルクの導出とその特性に関する問題です。
二次試験においてはトルクの導出は必須の知識となりますので,本問においてもできるだけ暗記に頼らず計算で導出できるようにしましょう。
特に(1)は計算しないと間違えやすい空欄と言えるかと思います。
1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は,
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \),回転子の回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
と定義されます。これを整理すると,
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ]
N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ]
&=&\left( 1-s \right) N_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
と同期速度から回転速度が導出できます。
3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
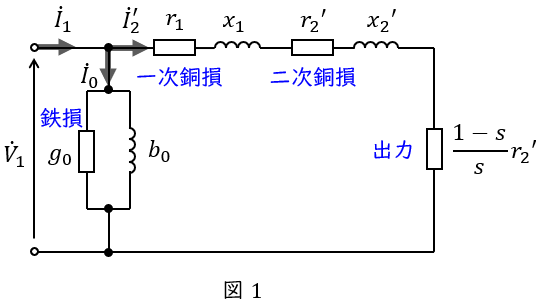
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
図1より,出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \),二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{\mathrm {c2}} &=& 3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導電動機の二次入力\( \ P_{2} \ \mathrm {[W]} \ \),出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)には,
\[
\begin{eqnarray}
P_{2}:P_{\mathrm {o}}:P_{\mathrm {c2}} &=& 1:(1-s):s \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かります。
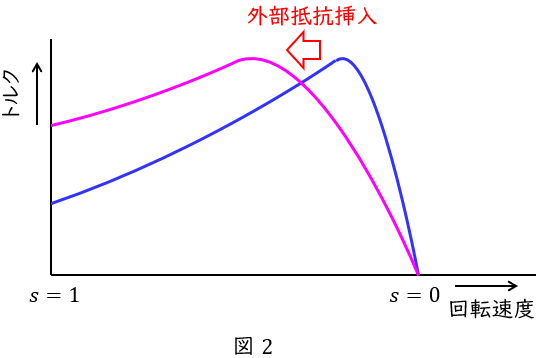
4.巻線形誘導電動機のトルクの比例推移
図1より,二次電流の一次換算値の大きさ\( \ I_{2}^{\prime } \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{2}^{\prime } &=& \frac {V_{1}}{\sqrt {\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
であるため,三相誘導電動機のトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は,
\[
\begin{eqnarray}
T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=&\frac {P_{2}\left( 1-s\right) }{\omega _{\mathrm {s}}\left( 1-s\right) } \\[ 5pt ]
&=&\frac {P_{2}}{\omega _{\mathrm {s}} } \\[ 5pt ]
&=&\frac {\displaystyle 3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2}}{\omega _{\mathrm {s}} } \\[ 5pt ]
&=& \frac {1}{\omega _{\mathrm {s}}}\frac {3V_{1}^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ 1≫s \ \)の時,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)以外の抵抗やリアクタンスは無視できるので,
\[
\begin{eqnarray}
T &≃& \frac {3V_{1}^{2}s}{\omega _{\mathrm {s}}r_{2}^{\prime }} \\[ 5pt ]
\end{eqnarray}
\]
となり,トルクに対する変数は可変抵抗(外部抵抗が挿入可能)である二次抵抗\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)と滑り\( \ s \ \)のみであり,トルク\( \ T \ \mathrm {[N\cdot m]} \ \)を一定とすると,
\[
\begin{eqnarray}
\frac {r_{2}^{\prime }}{s} &=& 一定 \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
(1)解答:ハ
題意より解答候補は,(ハ)\( \ 3V_{1}^{2} \ \),(ヘ)\( \ V_{1}^{2} \ \),(ヲ)\( \ 3V_{1}^{2}\left( 1-s \right) \ \),になると思います。
ワンポイント解説「4.巻線形誘導電動機のトルクの比例推移」の通り,トルクは\( \ \displaystyle T=\frac {1}{\omega _{0}}\cdot \frac {\boldsymbol {3V_{1}^{2}}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \ \)となります。
(2)解答:ヌ
題意より解答候補は,(ロ)\( \ s=1 \ \),(ト)\( \ s < 0 \ \),(ヌ)\( \ s > 0 \ \),になると思います。
ワンポイント解説「2.誘導機の滑り\( \ s \ \)」の通り,電動機運転においては回転速度\( \ N \ \)は同期速度\( \ N_{\mathrm {s}} \ \)より小さく\( \ s > 0 \ \)となります。
(3)解答:ル
題意より解答候補は,(ニ)同期,(ホ)脱出,(ル)停動,になると思います。
誘導電動機において,最大トルクは停動トルクと呼ばれます。
(4)解答:チ
題意より解答候補は,(イ)\( \ r_{1} \ \),(チ)\( \ r_{2}^{\prime } \ \),(カ)\( \ x_{2}^{\prime } \ \),になると思います。
\( \ \displaystyle s_{\mathrm {t}}=\frac {r_{2}^{\prime }}{\sqrt {r_{1}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}} \ \)をトルクの式に代入すると,最大トルク\( \ T_{\mathrm {t}} \ \mathrm {[N\cdot m]} \ \)は,
\[
\begin{eqnarray}
T_{\mathrm {t}} &=& \frac {1}{\omega _{0}}\cdot \frac {\displaystyle 3V_{1}^{2} \times \frac {r_{2}^{\prime }}{s_{\mathrm {t}}}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime }}{s_{\mathrm {t}}}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
&=& \frac {1}{\omega _{0}}\cdot \frac {\displaystyle 3V_{1}^{2} \times \frac {r_{2}^{\prime }}{\displaystyle \frac {r_{2}^{\prime }}{\sqrt {r_{1}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}}}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime }}{\displaystyle \frac {r_{2}^{\prime }}{\sqrt {r_{1}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}}}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
&=& \frac {1}{\omega _{0}}\cdot \frac {\displaystyle 3V_{1}^{2} \times \sqrt {r_{1}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}}{\displaystyle \left\{ r_{1}+\sqrt {r_{1}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}\right\} ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ r_{2}^{\prime } \ \)に関係なく一定となります。
(5)解答:ワ
題意より解答候補は,(リ)無関係である,(ワ)比例する,(ヨ)反比例する,になると思います。
ワンポイント解説「4.巻線形誘導電動機のトルクの比例推移」の通り,同期速度に近い範囲すなわち\( \ 1≫s \ \)では,トルク\( \ T \ \)は滑り\( \ s \ \)にほぼ比例します。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは