《機械・制御》〈変圧器〉[H19:問2]単相変圧器の各損失と効率に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

定格容量\( \ 500 \ \mathrm {[kV\cdot A]} \ \)，定格一次電圧\( \ 6 \ 600 \ \mathrm {[V]} \ \)，定格二次電圧\( \ 440 \ \mathrm {[V]} \ \)，定格周波数\( \ 60 \ \mathrm {[Hz]} \ \)の単相変圧器がある。この変圧器の一次巻線の抵抗は\( \ 0.625 \ \mathrm {[\Omega ]} \ \)，二次巻線の抵抗は\( \ 0.00224 \ \mathrm {[\Omega ]} \ \)である。この変圧器の二次側を開いて，一次側に定格周波数，定格一次電圧を印加して無負荷試験を行ったところ，一次側に\( \ 0.638 \ \mathrm {[A]} \ \)の電流が流れ，力率は\( \ 0.254 \ \)（遅れ）であった。この変圧器について，次の値を求めよ。ただし，この変圧器の鉄損と銅損以外の損失は小さいので無視できるものとする。また，答の有効数字は\( \ 5 \ \)けた目を四捨五入した\( \ 4 \ \)けたとする。

(1)　変圧器の鉄損\( \ \mathrm {[kW]} \ \)

(2)　変圧器を定格負荷で運転しているときの銅損\( \ \mathrm {[kW]} \ \)

(3)　変圧器を定格負荷，カ率\( \ 1 \ \)で運転しているときの効率\( \ \mathrm {[％]} \ \)

(4)　変圧器を力率\( \ 1 \ \)で運転しているときの最大効率\( \ \mathrm {[％]} \ \)

【ワンポイント解説】

変圧器の損失を効率を考える問題です。
本問で扱っている内容はいずれも\( \ 3 \ \)種でも学習する内容なので，多くの受験生が選択した問題と考えられます。
有効数字の指定がありケアレスミスが発生しやすいので，十分に注意するようにして下さい。

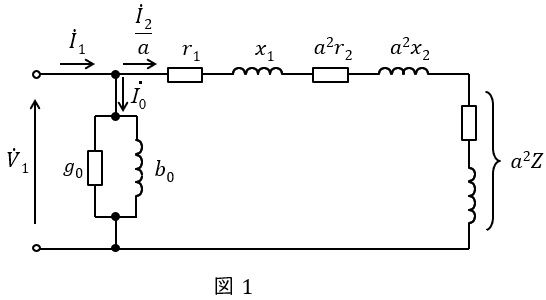
1.変圧器の\( \ \mathrm {L} \ \)形等価回路（一次換算）
変圧器の一次換算等価回路を図1に示します。ただし，\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流，\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)は二次電流，\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流，\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗，\( \ r_{2} \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗，\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス，\( \ x_{2} \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンス，\( \ a \ \)は変圧比（巻数比）となります。

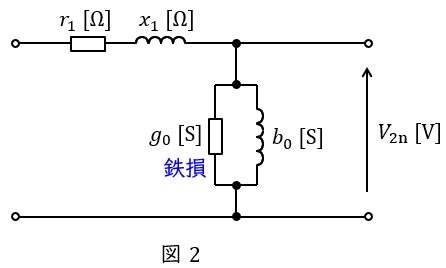
2.無負荷試験の等価回路
変圧器の無負荷試験は一次側を開放して，二次側に定格電圧を加える試験です。測定される電力は鉄損となり，測定される電力と電流から，励磁コンダクタンス\( \ g_{0} \ \mathrm {[S]} \ \)及び励磁サセプタンス\( \ b_{0} \ \mathrm {[S]} \ \)を求めることが可能となります。二次側に定格電圧を加えるのが一般的ですが，二次側開放で一次側に定格電圧を加えても同様に求められます。

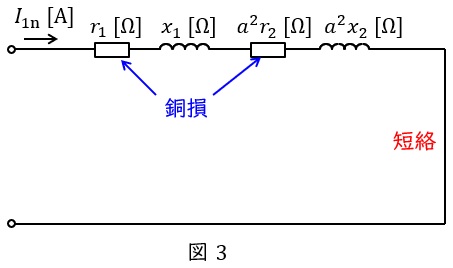
3.短絡試験の等価回路
変圧器の短絡試験は二次側を短絡して，一次側にインピーダンス電圧を加えて，定格電流を流す試験です。励磁回路に流れる電流が十分に小さいと仮定すると，測定される電力は銅損となります。測定される電力と電流から，高圧側換算の巻線抵抗\( \ R=r_{1}+a^{2}r_{2} \ \mathrm {[\Omega ]} \ \)及び漏れリアクタンス\( \ X=x_{1}+a^{2}x_{2} \ \mathrm {[\Omega ]} \ \)を求めることが可能となります。

4.変圧器の効率\( \ \eta \ \)と最大効率\( \ \eta _{\mathrm {m}} \ \)
変圧器の損失は鉄損\( \ p_{\mathrm {i}} \ \mathrm {[W]} \ \)と銅損\( \ p_{\mathrm {c}} \ \mathrm {[W]} \ \)があり，\( \ p_{\mathrm {i}} \ \mathrm {[W]} \ \)は負荷によらず一定であり，\( \ p_{\mathrm {c}} \ \mathrm {[W]} \ \)は負荷（電流）の\( \ 2 \ \)乗に比例します。従って，定格出力\( \ P_{\mathrm {n}} \ \mathrm {[W]} \ \)で利用率\( \ \alpha \ \)の時の変圧器の効率\( \ \eta \ \)は，
\[
\begin{eqnarray}
\eta &=&\frac {出力}{入力} \\[ 5pt ] &=&\frac {出力}{出力+損失} \\[ 5pt ] &=&\frac {\alpha P_{\mathrm {n}}}{\alpha P_{\mathrm {n}}+p_{\mathrm {i}}+\alpha ^{2}p_{\mathrm {c}}} \\[ 5pt ] \end{eqnarray}
\] となります。
次に，最大効率\( \ \eta _{\mathrm {m}} \ \)を求めます。上式の分母分子を\( \ \alpha \ \)で割ると
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {n}}}{\displaystyle P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}}} \\[ 5pt ] \end{eqnarray}
\] となり，効率が最大となるためには，上式の分母が最小となれば良いです。よって，\( \ \displaystyle A=P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}} \ \)と置くと，
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}\alpha }&=&-\frac {p_{\mathrm {i}}}{\alpha ^{2} }+p_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] となります。よって\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}\alpha }=0 \ \)となるとき，\( \ p_{\mathrm {i}}=\alpha ^{2}p_{\mathrm {c}} \ \)であり，鉄損と銅損が等しい時効率は最大となります。

【解答】

(1)変圧器の鉄損\( \ \mathrm {[kW]} \ \)
無負荷試験を行ったとき，定格一次電圧\( \ V_{1n}=6 \ 600 \ \mathrm {[V]} \ \)を加えると，一次側に\( \ I_{1}=0.638 \ \mathrm {[A]} \ \)の電流が流れ，力率が\( \ \cos \theta =0.254 \ \)（遅れ）となったので，変圧器の鉄損\( \ P_{i} \ \mathrm {[kW]} \ \)は，ワンポイント解説「2.無負荷試験の等価回路」の通り，
\[
\begin{eqnarray}
P_{i}&=&V_{1n}I_{1}\cos \theta \\[ 5pt ] &=&6 \ 600\times 0.638\times 0.254 \\[ 5pt ] &≒&1 \ 069.54 \ \mathrm {[W]}　→　1.069 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)変圧器を定格負荷で運転しているときの銅損\( \ \mathrm {[kW]} \ \)
定格一次電圧\( \ V_{1n}=6 \ 600 \ \mathrm {[V]} \ \)，定格二次電圧\( \ V_{2n}=440 \ \mathrm {[V]} \ \)なので，巻数比\( \ a \ \)は，
\[
\begin{eqnarray}
a&=&\frac {V_{1n}}{V_{2n}} \\[ 5pt ] &=&\frac {6 \ 600}{440} \\[ 5pt ] &=&15 \\[ 5pt ] \end{eqnarray}
\] となり，定格容量\( \ P_{n}=500 \ \mathrm {[kV\cdot A]} \ \)より，定格一次電流\( \ I_{1n} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{1n}&=&\frac {P_{n}}{V_{1n}} \\[ 5pt ] &=&\frac {500\times 10^{3}}{6 \ 600} \\[ 5pt ] &≒&75.757 \ 6 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，一次巻線抵抗\( \ r_{1}=0.625 \ \mathrm {[\Omega ]} \ \)，二次巻線抵抗\( \ r_{2}=0.002 \ 24 \ \mathrm {[\Omega ]} \ \)であるから，定格負荷で運転しているときの銅損\( \ P_{cn} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{cn}&=&\left( r_{1}+a^{2}r_{2}\right) {I_{1n}}^{2} \\[ 5pt ] &=&\left( 0.625+15^{2}\times 0.002 \ 24\right) \times 75.757 \ 6^{2} \\[ 5pt ] &≒&6 \ 479.57 \ \mathrm {[W]}　→　6.480 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)変圧器を定格負荷，カ率\( \ 1 \ \)で運転しているときの効率\( \ \mathrm {[％]} \ \)
定格負荷，カ率\( \ 1 \ \)なので，出力\( \ P_{o}=500 \ \mathrm {[kW]} \ \)であるから，このときの効率\( \ \eta \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
\eta &=&\frac {P_{o}}{P_{o}+P_{i}+P_{cn}}\times 100 \\[ 5pt ] &=&\frac {500\times 10^{3}}{500\times 10^{3}+1 \ 069.54+6 \ 479.57}\times 100 \\[ 5pt ] &≒&98.51 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)変圧器を力率\( \ 1 \ \)で運転しているときの最大効率\( \ \mathrm {[％]} \ \)
ワンポイント解説「4.変圧器の効率\( \ \eta \ \)と最大効率\( \ \eta _{\mathrm {m}} \ \)」の通り，変圧器の効率が最大となるのは鉄損と銅損が等しいときであるから，そのときの利用率を\( \ \alpha \ \)とすると，
\[
\begin{eqnarray}
P_{i}&=&\alpha ^{2}P_{cn} \\[ 5pt ] \alpha ^{2}&=&\frac {P_{i}}{P_{cn}} \\[ 5pt ] \alpha &=&\sqrt {\frac {P_{i}}{P_{cn}}} \\[ 5pt ] &=&\sqrt {\frac {1 \ 069.54}{6 \ 479.57}} \\[ 5pt ] &≒&0.406 \ 280 \\[ 5pt ] \end{eqnarray}
\] なので，最大効率\( \ \eta _{m} \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
\eta _{m}&=&\frac {\alpha P_{o}}{\alpha P_{o}+P_{i}+\alpha ^{2}P_{cn}}\times 100 \\[ 5pt ] &=&\frac {\alpha P_{o}}{\alpha P_{o}+2P_{i}}\times 100 \\[ 5pt ] &=&\frac {0.406 \ 280\times 500\times 10^{3}}{0.406 \ 280\times 500\times 10^{3}+2\times 1 \ 069.54}\times 100 \\[ 5pt ] &≒&98.96 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。