《理論》〈電磁気〉[H21:問2]空げきを含む磁気回路における巻線のインダクタンスに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，巻線のインダクタンスに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる数値（最も近い数値）を解答群の中から選び，その記号をマークシートに記入しなさい。

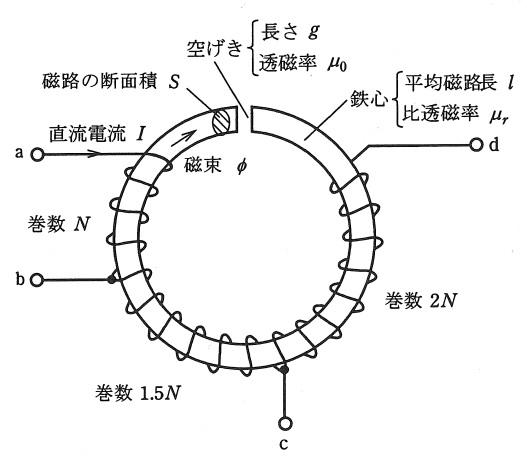
図のように，鉄心部と空げき部からなる磁路に巻線が巻かれている。鉄心部は，平均磁路長$ \ l \ $，比透磁率$ \ \mu_{r} \ $の鉄心から成っており，空げき部は，長さが$ \ g \ $で，透磁率が$ \ \mu_{0} \ $である。磁路の断面積は，鉄心部と空げき部ともに$ \ S \ $とする。巻線には，図のように端子$ \ \mathrm {a} \ $，$ \ \mathrm {b} \ $，$ \ \mathrm {c} \ $，$ \ \mathrm {d} \ $があり，$ \ \mathrm {a-b} \ $間に$ \ N \ $回，$ \ \mathrm {b-c} \ $間に$ \ 1.5N \ $回，$ \ \mathrm {c-d} \ $間に$ \ 2N \ $回が巻かれている。磁路において磁束は一様に分布し，漏れ磁束，磁気飽和，ヒステリシス，渦電流はないものとする。ここでは，次のように，磁路及び巻線の定数を定める。
　$ \ l=0.5 \ \mathrm {[m]} \ $，$ \ g=5\times 10^{-4} \ \mathrm {[m]} \ $，$ \ S=0.0012 \ \mathrm {[m^{2}]} \ $，$ \ \mu _{0}=4\pi \times 10^{-7} \ \mathrm {[H / m]} \ $，$ \ \mu _{r}=1 \ 000 \ $，$ \ N=30 \ $

図の巻線において，鉄心部の磁気抵抗は空げき部の磁気抵抗の$ \ \fbox {　（１）　} \ $倍である。$ \ \mathrm {b-c} \ $間の自己インダクタンスは$ \ \mathrm {a-b} \ $間の自己インダクタンスの$ \ \fbox {　（２）　} \ $倍である。また，$ \ \mathrm {b-c} \ $間と$ \ \mathrm {c-d} \ $間の巻線間の相互インダクタンスは，$ \ \mathrm {a-b} \ $間の自己インダクタンスの$ \ \fbox {　（３）　} \ $倍である。

次に，端子$ \ \mathrm {b} \ $及び$ \ \mathrm {c} \ $を非接続のまま，$ \ \mathrm {a-d} \ $間に直流電流$ \ I=3 \ \mathrm {[A]} \ $を図の向きに流すとき，磁路の磁束は$ \ \fbox {　（４）　} \ \mathrm {[Wb]} \ $である。また，この接続において，磁路の磁束密度が$ \ 1 \ \mathrm {[T]} \ $となるときの電流は，$ \ \fbox {　（５）　} \ \mathrm {[A]} \ $である。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　8.7\times 10^{-4}　　　　　&（ロ）&　1.5　　　　　&（ハ）&　6.1\times 10^{-4} \\[ 5pt ] &（ニ）&　2.5　　　　　&（ホ）&　4　　　　　&（ヘ）&　3 \\[ 5pt ] &（ト）&　5.9　　　　　&（チ）&　0.5　　　　　&（リ）&　3.8\times 10^{-4} \\[ 5pt ] &（ヌ）&　0.09　　　　　&（ル）&　34　　　　　&（ヲ）&　1.88 \\[ 5pt ] &（ワ）&　1　　　　　&（カ）&　1.22　　　　　&（ヨ）&　2.25 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

空げきを含む磁気回路における巻線のインダクタンスに関する問題です。
本問の場合，数値が全て与えられていますが，計算の工夫として直前までは文字のまま計算し，最後に代入する方がミスなく早く解けると思います。$ \ 10～15 \ $分程度で解く必要がありますので，ぜひ計算テクニックは磨いていくようにして下さい。

1.自己インダクタンスの定義$ \ L \ $
巻数$ \ N \ $のコイルに電流$ \ I \ \mathrm {[A]} \ $を流した時の鎖交磁束が$ \ \phi \ \mathrm {[Wb]} \ $であった時，自己インダクタンス$ \ L \ \mathrm {[H]} \ $と鎖交磁束$ \ \phi \ \mathrm {[Wb]} \ $の関係は，
\[
\begin{eqnarray}
LI&=&N\phi \\[ 5pt ] \end{eqnarray}
\] となります。

2.相互インダクタンス$ \ M \ $
自己インダクタンス$ \ L_{1} \ \mathrm {[H]} \ $と$ \ L_{2} \ \mathrm {[H]} \ $のコイルがあった時，コイル間の相互インダクタンス$ \ M \ \mathrm {[H]} \ $は，
\[
\begin{eqnarray}
M&=&k\sqrt {L_{1}L_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。この時，$ \ k \ $は結合係数と呼ばれ，$ \ 0≦k≦1 \ $となります。

3.磁気回路のオームの法則
中心長さ$ \ l \ \mathrm {[ m ]} \ $の環状鉄心に巻数$ \ N \ $のコイルが巻かれ，そこに電流$ \ I \ \mathrm {[ A ]} \ $が流れている時，鉄心内の磁界の強さ$ \ H \ \mathrm {[ A / m ]} \ $は，アンペールの周回積分の法則より，
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ] H&=&\frac {NI}{l} \\[ 5pt ] \end{eqnarray}
\] であるから，鉄心内の磁束密度$ \ B \ \mathrm {[ T ]} \ $は，鉄心内の透磁率$ \ \mu \ \mathrm {[ H / m ]} \ $とすると，
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ] &=&\frac {\mu NI}{l} \\[ 5pt ] \end{eqnarray}
\] となります。鉄心内の磁束$ \ \phi \ \mathrm {[ Wb ]} \ $は，鉄心の断面積$ \ S \ \mathrm {[ m^{2} ]} \ $とすると，
\[
\begin{eqnarray}
\phi &=&BS \\[ 5pt ] &=&\frac {\mu NIS}{l} \\[ 5pt ] &=&\frac {NI}{\displaystyle \frac {l}{\mu S}} \\[ 5pt ] \end{eqnarray}
\] となり，起磁力$ \ F=NI \ \mathrm {[ A ]} \ $，磁気抵抗$ \ R_{\mathrm {m}}=\displaystyle \frac {l}{\mu S} \ \mathrm {[ H^{-1} ]} \ $とすると，
\[
\begin{eqnarray}
\phi &=&\frac {F}{R_{\mathrm {m}}} \\[ 5pt ] \end{eqnarray}
\] となり，磁気回路のオームの法則が成立します。また，このときの自己インダクタンス$ \ L \ \mathrm {[H]} \ $は，
\[
\begin{eqnarray}
L &=&\frac {N\phi }{I} \\[ 5pt ] &=&\frac {\displaystyle N\cdot \frac {NI}{R_{\mathrm {m}}}}{I} \\[ 5pt ] &=&\frac {N^{2}}{R_{\mathrm {m}}} \\[ 5pt ] &=&\frac {N^{2}}{\displaystyle \frac {l}{\mu S} } \\[ 5pt ] &=&\frac {\mu SN^{2}}{l} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ワ
鉄心部の磁気抵抗$ \ R_{\mathrm {m}} \ \mathrm {[ H^{-1} ]} \ $及び空げき部の磁気抵抗$ \ R_{\mathrm {g}} \ \mathrm {[ H^{-1} ]} \ $とすると，その比$ \ \displaystyle \frac {R_{\mathrm {m}}}{R_{\mathrm {g}}} \ $は，ワンポイント解説「3.磁気回路のオームの法則」の通り，
\[
\begin{eqnarray}
\frac {R_{\mathrm {m}}}{R_{\mathrm {g}}} &=&\frac {\displaystyle \frac {l}{\mu _{0}\mu _{r} S}}{\displaystyle \frac {g}{\mu _{0}S}} \\[ 5pt ] &=&\frac {l}{\mu _{r}g} \\[ 5pt ] &=&\frac {0.5}{1 \ 000\times 5\times 10^{-4}} \\[ 5pt ] &=&1 \\[ 5pt ] \end{eqnarray}
\] となり，鉄心部の磁気抵抗$ \ R_{\mathrm {m}} \ \mathrm {[ H^{-1} ]} \ $は空げき部の磁気抵抗$ \ R_{\mathrm {g}} \ \mathrm {[ H^{-1} ]} \ $の$ \ 1 \ $倍であることがわかる。

(2)解答：ヨ
磁気回路において，自己インダクタンス$ \ L \ \mathrm {[H]} \ $は，ワンポイント解説「3.磁気回路のオームの法則」の通り，
\[
\begin{eqnarray}
L &=&\frac {N\phi }{I} \\[ 5pt ] &=&\frac {\displaystyle N\cdot \frac {NI}{R_{\mathrm {m}}}}{I} \\[ 5pt ] &=&\frac {N^{2}}{R_{\mathrm {m}}} \\[ 5pt ] \end{eqnarray}
\] となり，巻数$ \ N \ $の$ \ 2 \ $乗に比例するので，$ \ \mathrm {b-c} \ $間の自己インダクタンス$ \ L_{\mathrm {bc}} \ \mathrm {[H]} \ $と$ \ \mathrm {a-b} \ $間の自己インダクタンス$ \ L_{\mathrm {ab}} \ \mathrm {[H]} \ $の比$ \ \displaystyle \frac {L_{\mathrm {bc}}}{L_{\mathrm {ab}}} \ $は，
\[
\begin{eqnarray}
\frac {L_{\mathrm {bc}}}{L_{\mathrm {ab}}} &=&\frac {\left( 1.5N\right) ^{2}}{N^{2}} \\[ 5pt ] &=&2.25 \\[ 5pt ] \end{eqnarray}
\] となり，$ \ \mathrm {b-c} \ $間の自己インダクタンス$ \ L_{\mathrm {bc}} \ \mathrm {[H]} \ $は$ \ \mathrm {a-b} \ $間の自己インダクタンス$ \ L_{\mathrm {ab}} \ \mathrm {[H]} \ $の$ \ 2.25 \ $倍であることがわかる。

(3)解答：ヘ
(2)と同様に，$ \ \mathrm {c-d} \ $間の自己インダクタンス$ \ L_{\mathrm {cd}} \ \mathrm {[H]} \ $と$ \ \mathrm {a-b} \ $間の自己インダクタンス$ \ L_{\mathrm {ab}} \ \mathrm {[H]} \ $の比$ \ \displaystyle \frac {L_{\mathrm {cd}}}{L_{\mathrm {ab}}} \ $は，
\[
\begin{eqnarray}
\frac {L_{\mathrm {cd}}}{L_{\mathrm {ab}}} &=&\frac {\left( 2N\right) ^{2}}{N^{2}} \\[ 5pt ] &=&4 \\[ 5pt ] \end{eqnarray}
\] であるため，$ \ \mathrm {b-c} \ $間と$ \ \mathrm {c-d} \ $間の巻線間の相互インダクタンス$ \ M \ \mathrm {[H]} \ $は，漏れ磁束，磁気飽和，ヒステリシス，渦電流はないので結合係数$ \ k=1 \ $と考えれば良いから，ワンポイント解説「2.相互インダクタンス$ \ M \ $」の通り，
\[
\begin{eqnarray}
M &=&k\sqrt {L_{\mathrm {bc}}L_{\mathrm {cd}}} \\[ 5pt ] &=&1\times \sqrt {2.25L_{\mathrm {ab}}\times 4L_{\mathrm {ab}}} \\[ 5pt ] &=&\sqrt {9{L_{\mathrm {ab}}}^{2}} \\[ 5pt ] &=&3L_{\mathrm {ab}} \\[ 5pt ] \end{eqnarray}
\] となり，$ \ \mathrm {b-c} \ $間と$ \ \mathrm {c-d} \ $間の巻線間の相互インダクタンス$ \ M \ \mathrm {[H]} \ $は，$ \ \mathrm {a-b} \ $間の自己インダクタンス$ \ L_{\mathrm {ab}} \ \mathrm {[H]} \ $の$ \ 3 \ $倍であることがわかる。

(4)解答：ハ
$ \ \mathrm {a-d} \ $間の巻数は$ \ N+1.5N+2N=4.5N \ $であるので，磁路の磁束$ \ \phi \ \mathrm {[Wb]} \ $は，ワンポイント解説「3.磁気回路のオームの法則」の通り，
\[
\begin{eqnarray}
\phi &=&\frac {4.5NI}{R_{\mathrm {m}}+R_{\mathrm {g}}} \\[ 5pt ] &=&\frac {4.5NI}{2R_{\mathrm {m}}} \\[ 5pt ] &=&\frac {4.5NI}{\displaystyle 2\cdot \frac {l}{\mu _{0}\mu _{r}S}} \\[ 5pt ] &=&\frac {4.5NI\mu _{0}\mu _{r}S}{2l}　　　・・・・・・・・・　① \\[ 5pt ] &=&\frac {4.5\times 30\times 3\times 4\pi \times 10^{-7}\times 1 \ 000\times 0.0012}{2\times 0.5} \\[ 5pt ] &≒&6.11\times 10^{-4} \ \mathrm {[Wb]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ト
磁束密度$ \ B=1 \ \mathrm {[T]} \ $のときの磁束$ \ \phi \ \mathrm {[Wb]} \ $は，
\[
\begin{eqnarray}
\phi &=&BS \\[ 5pt ] &=&1\times 0.0012 \\[ 5pt ] &=&0.0012 \ \mathrm {[Wb]} \\[ 5pt ] \end{eqnarray}
\] であるため，このときの電流$ \ I \ \mathrm {[A]} \ $は，①を変形すると，
\[
\begin{eqnarray}
\phi &=&\frac {4.5NI\mu _{0}\mu _{r}S}{2l} \\[ 5pt ] I&=&\frac {2l\phi }{4.5N\mu _{0}\mu _{r}S} \\[ 5pt ] &=&\frac {2\times 0.5\times 0.0012 }{4.5\times 30 \times 4\pi \times 10^{-7}\times 1 \ 000\times 0.0012} \\[ 5pt ] &≒&5.89 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。