Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,三相回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
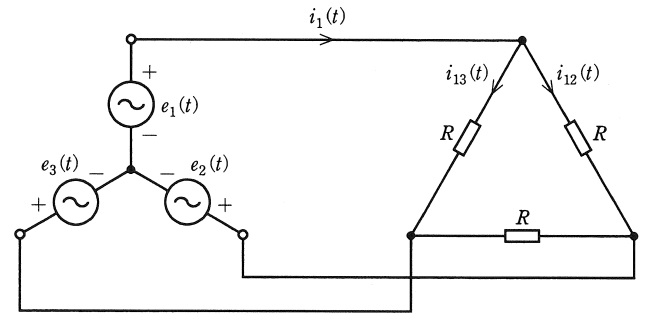
図に示す回路において,定常状態における\( \ i_{1}\left( t\right) \ \),\( \ i_{12}\left( t\right) \ \),\( \ i_{13}\left( t\right) \ \)の実効値を求めたい。ただし,\( \ e_{1}\left( t\right) =\sqrt {2}E \cos \omega t \ \),\( \ \displaystyle e_{2}\left( t\right) =\sqrt {2}E \cos \left( \omega t-\frac {2}{3}\pi \right) \ \),\( \ \displaystyle e_{3}\left( t\right) =\sqrt {2}E \cos \left( \omega t-\frac {4}{3}\pi \right) \ \)とする。
まず,電源\( \ e_{1}\left( t\right) \ \),\( \ e_{2}\left( t\right) \ \)の電圧ベクトルを,それぞれ\( \ {\dot E}_{1}=E\mathrm {e}^{\mathrm {j}0} \ \),\( \ {\dot E}_{2}=E\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi } \ \)と書き表すと,\( \ e_{3}\left( t\right) \ \)の電圧ベクトルは\( \ {\dot E}_{3}= \ \fbox { (1) } \ \)と表される。次に,\( \ i_{1}\left( t\right) =\sqrt {2}I_{1} \cos \left( \omega t+\varphi _{1}\right) \ \),\( \ i_{12}\left( t\right) =\sqrt {2}I_{12} \cos \left( \omega t+\varphi _{12}\right) \ \),\( \ i_{13}\left( t\right) =\sqrt {2}I_{13} \cos \left( \omega t+\varphi _{13}\right) \ \)とおき,それぞれの電流ベクトルを\( \ {\dot I}_{1} \ \),\( \ {\dot I}_{12} \ \),\( \ {\dot I}_{13} \ \)とする。このとき,\( \ {\dot I}_{12}= \ \fbox { (2) } \ \),\( \ {\dot I}_{13}= \ \fbox { (3) } \ \),\( \ {\dot I}_{1}= \ \fbox { (4) } \ \)となり,これより\( \ I_{12}=\left| {\dot I}_{12}\right| = \ \fbox { (5) } \ \),\( \ I_{13}=\left| {\dot I}_{13}\right| = \ \fbox { (5) } \ \),\( \ I_{1}=\left| {\dot I}_{1}\right| = \ \fbox { (4) } \ \)となる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {E}{R}\left( 2-\mathrm {e}^{-\mathrm {j}\frac {\pi }{3}}-\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi }\right) &(ロ)& E\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi } &(ハ)& \frac {E}{R}\left( 1-\mathrm {e}^{-\mathrm {j}\frac {\pi }{3}}\right) \\[ 5pt ]
&(ニ)& E\mathrm {e}^{-\mathrm {j}\pi } &(ホ)& \frac {3E}{R} &(ヘ)& E\mathrm {e}^{-\mathrm {j}2\pi } \\[ 5pt ]
&(ト)& \frac {E}{R}\left( 1-\mathrm {e}^{-\mathrm {j}\frac {5}{3}\pi }\right) &(チ)& \frac {E}{R}\left( 2-\mathrm {e}^{-\mathrm {j}0}\right) &(リ)& \frac {E}{R}\left( 1-\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi }\right) \\[ 5pt ]
&(ヌ)& \frac {E}{R}\left( 2-\mathrm {e}^{-\mathrm {j}\pi}-\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi }\right) &(ル)& \frac {\sqrt {6}E}{R} &(ヲ)& \frac {E}{R}\left( 1-\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi }\right) \\[ 5pt ]
&(ワ)& \frac {\sqrt {2}E}{R} &(カ)& \frac {E}{R}\left( 2-\mathrm {e}^{-\mathrm {j}\pi }\right) &(ヨ)& \frac {\sqrt {3}E}{R} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
三相交流回路の複素演算に関する問題です。
難易度は普通としていますが,複素表示に慣れている受験生はほぼ完答,慣れていない受験生は全くできないという問題となり,点数差が開く問題と言えます。
1.オイラーの公式
複素計算で用いるオイラーの公式は以下の通りとなります。
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ]
\mathrm {e}^{\mathrm {-j}\theta }&=&\cos \theta -\mathrm {j}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
2.瞬時値表示とベクトル表示
三相交流には瞬時値表示による方法とベクトル表示による方法があり,どちらもしっかりと理解し使いこなせるようにしておく必要があります。
①瞬時値表示
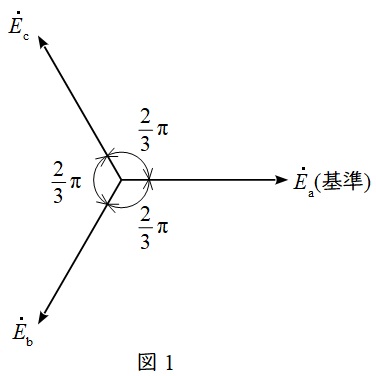
図1のような三相対称交流があるとし,それぞれの電圧の実効値が\( \ E \ \mathrm {[V]} \ \)であるとすれば,基準電圧である\( \ \mathrm {a} \ \)相の電圧\( \ {\dot E}_{\mathrm {a}} \ \mathrm {[V]} \ \)の瞬時値\( \ e_{\mathrm {a}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
e_{\mathrm {a}}&=&\sqrt {2}E\sin \omega t \\[ 5pt ]
\end{eqnarray}
\]
で表すことができ,\( \ \mathrm {b} \ \)相,\( \ \mathrm {c} \ \)相はそこから\( \ \displaystyle \frac {2}{3}\pi \ \mathrm {[rad]} \ \)ずつ位相が遅れているので,
\[
\begin{eqnarray}
e_{\mathrm {b}}&=&\sqrt {2}E\sin \left( \omega t-\frac {2}{3}\pi \right) \\[ 5pt ]
e_{\mathrm {c}}&=&\sqrt {2}E\sin \left( \omega t-\frac {4}{3}\pi \right) \\[ 5pt ]
\end{eqnarray}
\]
と表すことができます。
②ベクトル表示
瞬時値表示と同様,それぞれの電圧の実効値が\( \ E \ \mathrm {[V]} \ \)であるとすれば,基準電圧である\( \ \mathrm {a} \ \)相の電圧\( \ {\dot E}_{\mathrm {a}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {a}}&=&E∠0&=&E\mathrm {e}^{\mathrm {j}0} \\[ 5pt ]
\end{eqnarray}
\]
で表すことができ,\( \ \mathrm {b} \ \)相,\( \ \mathrm {c} \ \)相はそこから\( \ \displaystyle \frac {2}{3}\pi \ \mathrm {[rad]} \ \)ずつ位相が遅れているので,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {b}}&=&E∠\left( -\mathrm {j}\frac {2}{3}\pi \right) &=&E\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi } \\[ 5pt ]
{\dot E}_{\mathrm {c}}&=&E∠\left( -\mathrm {j}\frac {4}{3}\pi \right) &=&E\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi } \\[ 5pt ]
\end{eqnarray}
\]
と表すことができます。これらにオイラーの公式を適用すると,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {a}}&=&E\left( \cos 0 +\mathrm {j}\sin 0 \right) \\[ 5pt ]
&=&E \\[ 5pt ]
{\dot E}_{\mathrm {b}}&=&E\left\{ \cos \left( -\frac {2}{3}\pi \right) +\mathrm {j}\sin \left( -\frac {2}{3}\pi \right) \right\} \\[ 5pt ]
&=&E\left( -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \right) \\[ 5pt ]
{\dot E}_{\mathrm {c}}&=&E\left\{ \cos \left( -\frac {4}{3}\pi \right) +\mathrm {j}\sin \left( -\frac {4}{3}\pi \right) \right\} \\[ 5pt ]
&=&E\left( -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ロ
ワンポイント解説「2.瞬時値表示とベクトル表示」の通り,\( \ e_{3}\left( t\right) \ \)の電圧ベクトル\( \ {\dot E}_{3} \ \)は,\( \ {\dot E}_{2} \ \)より\( \ \displaystyle \frac {2}{3}\pi \ \mathrm {[rad]} \ \)位相が遅れているので,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {3}}&=&E\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi } \\[ 5pt ]
\end{eqnarray}
\]
と表される。
(2)解答:ヲ
問題の回路図より,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {12}}&=&\frac {{\dot E}_{\mathrm {1}}-{\dot E}_{\mathrm {2}}}{R} \\[ 5pt ]
&=&\frac {E\mathrm {e}^{\mathrm {j}0 }-E\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi }}{R} \\[ 5pt ]
&=&\frac {E-E\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi }}{R} \\[ 5pt ]
&=&\frac {E}{R}\left( 1-\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi }\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:リ
(2)と同様に,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {13}}&=&\frac {{\dot E}_{\mathrm {1}}-{\dot E}_{\mathrm {3}}}{R} \\[ 5pt ]
&=&\frac {E\mathrm {e}^{\mathrm {j}0 }-E\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi }}{R} \\[ 5pt ]
&=&\frac {E-E\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi }}{R} \\[ 5pt ]
&=&\frac {E}{R}\left( 1-\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi }\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ホ
問題図より,\( \ {\dot I}_{\mathrm {1}}={\dot I}_{\mathrm {12}}+{\dot I}_{\mathrm {13}} \ \)であるから,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {1}}&=&{\dot I}_{\mathrm {12}}+{\dot I}_{\mathrm {13}} \\[ 5pt ]
&=&\frac {E}{R}\left( 1-\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi }\right) +\frac {E}{R}\left( 1-\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi }\right) \\[ 5pt ]
&=&\frac {E}{R}\left( 2-\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi }-\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi } \right) \\[ 5pt ]
&=&\frac {E}{R}\left\{ 3-\left( 1+\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi }+\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi }\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,図1に示す通り,\( 1+\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi }+\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi }=0 \ \)であることを利用すれば,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {1}}&=&\frac {E}{R}\left( 3-0 \right) \\[ 5pt ]
&=&\frac {3E}{R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヨ
ワンポイント解説「1.オイラーの公式」より,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {12}}&=&\frac {E}{R}\left( 1-\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi }\right) \\[ 5pt ]
&=&\frac {E}{R}\left\{ 1-\left( -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2}\right) \right\} \\[ 5pt ]
&=&\frac {E}{R}\left( \frac {3}{2}+\mathrm {j}\frac {\sqrt {3}}{2}\right) \\[ 5pt ]
&=&\frac {E}{2R}\left( 3+\mathrm {j}\sqrt {3}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさ\( \ I_{12} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {12}}&=&\left| {\dot I}_{\mathrm {12}}\right| \\[ 5pt ]
&=&\frac {E}{2R}\sqrt {3^{2}+\left( \sqrt {3}\right) ^{2}} \\[ 5pt ]
&=&\frac {E}{2R}\times 2\sqrt {3} \\[ 5pt ]
&=&\frac {\sqrt {3}E}{R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは