Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,交流ブリッジと浮遊容量に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
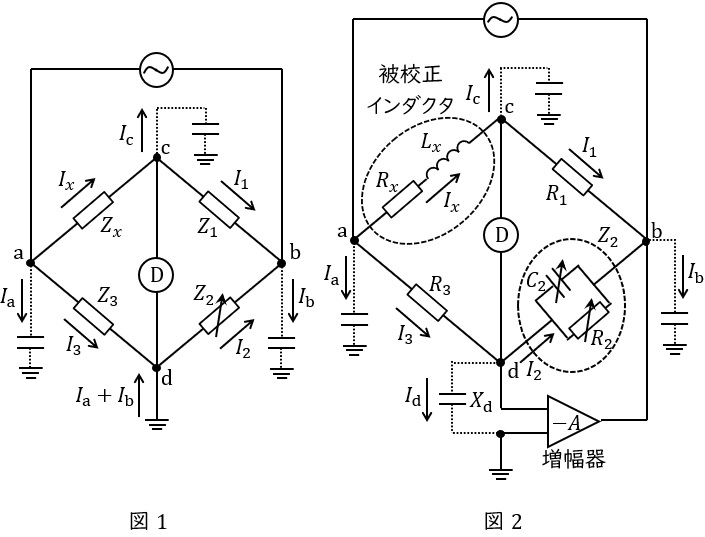
図1は,インピーダンス\( \ Z_{x} \ \)を校正するための交流ブリッジで,既知の標準インピーダンス\( \ Z_{1} \ \),\( \ Z_{2} \ \),\( \ Z_{3} \ \),検出器Ⓓ及び電源で構成される。なお,\( \ I_{x} \ \),\( \ I_{1} \ \),\( \ I_{2} \ \),\( \ I_{3} \ \)は\( \ 4 \ \)辺を流れる電流,\( \ I_{\mathrm {a}} \ \),\( \ I_{\mathrm {b}} \ \),\( \ I_{\mathrm {c}} \ \)は浮遊容量を通じてグランドへ流れる漏れ電流である。
まず,図1から浮遊容量を除去した回路を考える。\( \ Z_{2} \ \)を調整してⒹが零を指したとき,電流は\( \ I_{x}=I_{1} \ \),\( \ I_{2}=I_{3} \ \)のように均衡し,校正値は\( \ \displaystyle Z_{x}=\frac {Z_{1}Z_{3}}{Z_{2}} \ \)で得られる。
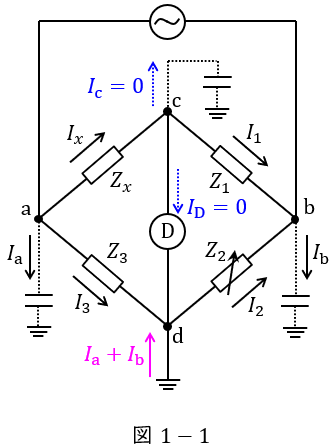
次に,図1のとおりに浮遊容量を有する回路で,Ⓓが零を指した場合を考える。このとき,\( \ \mathrm {c} \ \)とグランドは等電位なので\( \ I_{\mathrm {c}}=0 \ \)である。一方,\( \ \mathrm {a} \ \)及び\( \ \mathrm {b} \ \)は,グランドに対して電位差を持つため,\( \ I_{\mathrm {a}} \ \)及び\( \ I_{\mathrm {b}} \ \)(ただし,\( \ I_{\mathrm {a}}+I_{\mathrm {b}}≠0 \ \))が流れる。よって,\( \ 4 \ \)辺の電流の均衡は\( \ \fbox { (1) } \ \)のように崩れ,その結果,校正誤差が生じる。ゆえに,漏れ電流起因の校正誤差を減ずるための仕組みが必要になる。
一例を図2に示す。この回路は,インダクタ(抵抗\( \ R_{x} \ \)とインダクタンス\( \ L_{x} \ \)の直列)を校正するのに用いられる\( \ \fbox { (2) } \ \)ブリッジに,増幅率が\( \ -A \ \)の増幅器を図のように付加したものである。なお,\( \ \mathrm {d} \ \)は接地されておらず,容量性リアクタンス\( \ X_{\mathrm {d}} \ \)を通じて漏れ電流\( \ I_{\mathrm {d}} \ \)が流れる。また,Ⓓは零を指している。
\( \ R_{2} \ \)と\( \ C_{2} \ \)の合成インピーダンスを\( \ Z_{2} \ \),\( \ \mathrm {b} \ \)及び\( \ \mathrm {d} \ \)の電位を,それぞれ,\( \ V_{\mathrm {b}} \ \)及び\( \ V_{\mathrm {d}} \ \)とすれば,\( \ V_{\mathrm {b}}=-AV_{\mathrm {d}} \ \),\( \ V_{\mathrm {d}}=X_{\mathrm {d}}I_{\mathrm {d}} \ \),\( \ V_{\mathrm {d}}-V_{\mathrm {b}}=Z_{2}I_{2} \ \)であるから,次式が求められる。
\[
\begin{eqnarray}
\frac {I_{\mathrm {d}}}{I_{\mathrm {2}}}&=& \ \fbox { (3) } \ \\[ 5pt ]
\end{eqnarray}
\]
上式において,\( \ A \ \)が十分に大きい場合,\( \ I_{\mathrm {d}}=0 \ \)と見なせるので,\( \ I_{\mathrm {2}}=I_{\mathrm {3}} \ \)が成立する。さらに,\( \ V_{\mathrm {d}}=0 \ \)と見なせるので,\( \ \mathrm {c} \ \)及び\( \ \mathrm {d} \ \)はグランドと等電位になる。よって,\( \ I_{\mathrm {c}}=0 \ \)となるから,\( \ I_{x}=I_{1} \ \)が成立する。
このように,図2の校正回路は,漏れ電流の影響を受けずに\( \ 4 \ \)辺の電流が均衡する。そして,インダクタの校正値である\( \ R_{x}= \ \fbox { (4) } \ \ \),\( \ L_{x}= \ \fbox { (5) } \ \ \)が得られる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& シェーリング &(ロ)& ケルビンダブル &(ハ)& マクスウェル \\[ 5pt ]
&(ニ)& I_{x}≠I_{1},I_{2}≠I_{3} &(ホ)& I_{x}≠I_{1},I_{2}=I_{3} &(ヘ)& I_{x}=I_{1},I_{2}≠I_{3} \\[ 5pt ]
&(ト)& \frac {R_{2}R_{3}}{R_{1}} &(チ)& \frac {R_{1}R_{3}}{R_{2}} &(リ)& C_{2}R_{1}R_{2}R_{3} \\[ 5pt ]
&(ヌ)& \frac {R_{1}R_{2}}{R_{3}} &(ル)& \frac {1}{A}\frac {Z_{2}}{X_{\mathrm {d}}} &(ヲ)& C_{2}R_{1}R_{3} \\[ 5pt ]
&(ワ)& \frac {1}{A+1}\frac {Z_{2}}{X_{\mathrm {d}}} &(カ)& A\frac {Z_{2}}{X_{\mathrm {d}}} &(ヨ)& C_{2}R_{2}R_{3} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
交流ブリッジ回路を用いてインダクタンスの校正を行う回路の計算問題です。
ブリッジ回路は様々な回路があるため,すべての回路の名称を求めるのは大変と思いますが,平衡条件の考え方はどの回路も同じとなります。したがって,計算方法はあらゆる回路で応用できますので,ぜひマスターして得点源とするようにして下さい。
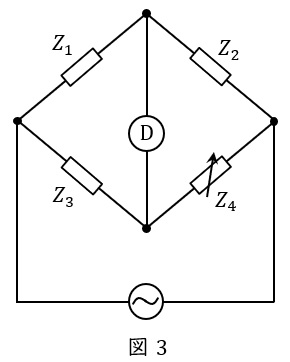
1.交流ブリッジ回路の平衡条件
図3の回路において,検流計Ⓓに電流が流れないようにしたとき,各インピーダンスの関係は,
\[
\begin{eqnarray}
{\dot Z}_{1}{\dot Z}_{4}&=&{\dot Z}_{2}{\dot Z}_{3} \\[ 5pt ]
\end{eqnarray}
\]
となります。これをブリッジの平衡条件といい,コンデンサの静電容量を求めるシェーリングブリッジ,電源の周波数を求めるウィーンブリッジ,コイルのインダクタンスを求めるヘイブリッジ,等様々な測定に利用されています。
【解答】
(1)解答:ヘ
題意に沿って,平衡条件が成立しているときの各電流値を記載すると図1-1のようになる。キルヒホッフの法則の電流則より,
\[
\begin{eqnarray}
I_{x}&=&I_{1},I_{2}&≠&I_{3} \\[ 5pt ]
\end{eqnarray}
\]
の関係があることがわかる。
(2)解答:ハ
題意より解答候補は,(イ)シェーリング,(ロ)ケルビンダブル,(ハ)マクスウェル,になると思います。
本問のような回路で,主にインダクタンスを測定するブリッジをマクスウェルブリッジといいます。
シェーリングブリッジはコンデンサの静電容量を求めるブリッジで平成26年問6に,ケルビンダブルブリッジは抵抗を測定するブリッジで1種平成21年問4に出題されたことがあります。
(3)解答:ワ
題意に沿って,\( \ V_{\mathrm {b}}=-AV_{\mathrm {d}} \ \)及び\( \ V_{\mathrm {d}}=X_{\mathrm {d}}I_{\mathrm {d}} \ \)を\( \ V_{\mathrm {d}}-V_{\mathrm {b}}=Z_{2}I_{2} \ \)に代入すれば,
\[
\begin{eqnarray}
V_{\mathrm {d}}-V_{\mathrm {b}}&=&Z_{2}I_{2} \\[ 5pt ]
X_{\mathrm {d}}I_{\mathrm {d}}+AV_{\mathrm {d}}&=&Z_{2}I_{2} \\[ 5pt ]
X_{\mathrm {d}}I_{\mathrm {d}}+AX_{\mathrm {d}}I_{\mathrm {d}}&=&Z_{2}I_{2} \\[ 5pt ]
X_{\mathrm {d}}I_{\mathrm {d}}\left( 1+A\right) &=&Z_{2}I_{2} \\[ 5pt ]
\frac {I_{\mathrm {d}}}{I_{2}} &=&\frac {1}{A+1}\frac {Z_{2}}{X_{\mathrm {d}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:チ
漏れ電流の影響を受けずに\( \ 4 \ \)辺の電流が均衡した回路においては,ブリッジの平衡条件が成立するので,電源の角周波数を\( \ \omega \ \)とすれば,ワンポイント解説「1.交流ブリッジ回路の平衡条件」の通り,
\[
\begin{eqnarray}
\left( R_{x}+\mathrm {j}\omega L_{x}\right) \left( \frac {\displaystyle R_{2}\cdot \frac {1}{\mathrm {j}\omega C_{2}}}{\displaystyle R_{2}+ \frac {1}{\mathrm {j}\omega C_{2}} }\right)&=&R_{1}R_{3} \\[ 5pt ]
\left( R_{x}+\mathrm {j}\omega L_{x}\right) \left( \frac {\displaystyle \frac {R_{2}}{\mathrm {j}\omega C_{2}}}{\displaystyle \frac {1+\mathrm {j}\omega C_{2}R_{2}}{\mathrm {j}\omega C_{2}} }\right)&=&R_{1}R_{3} \\[ 5pt ]
\left( R_{x}+\mathrm {j}\omega L_{x}\right) \frac {R_{2}}{1+\mathrm {j}\omega C_{2}R_{2}}&=&R_{1}R_{3} \\[ 5pt ]
\left( R_{x}+\mathrm {j}\omega L_{x}\right) R_{2}&=&R_{1}R_{3}\left( 1+\mathrm {j}\omega C_{2}R_{2}\right) \\[ 5pt ]
R_{x}R_{2}+\mathrm {j}\omega L_{x}R_{2}&=& R_{1}R_{3}+\mathrm {j}\omega C_{2}R_{1}R_{2}R_{3} \\[ 5pt ]
\end{eqnarray}
\]
となる。実部虚部について,それぞれ等しくなければならないので,実部を比較すれば,
\[
\begin{eqnarray}
R_{x}R_{2}&=& R_{1}R_{3} \\[ 5pt ]
R_{x}&=& \frac {R_{1}R_{3}}{R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヲ
(4)と同様にブリッジの平衡条件の虚部を比較すれば,
\[
\begin{eqnarray}
\omega L_{x}R_{2}&=&\omega C_{2}R_{1}R_{2}R_{3} \\[ 5pt ]
L_{x}&=&C_{2}R_{1}R_{3} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは