《理論》〈電子理論〉[R06:問8]負帰還増幅回路における電圧増幅率に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，負帰還増幅回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

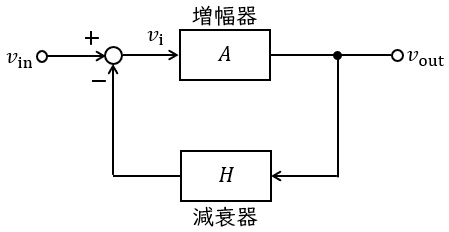
図は負帰還増幅回路を表すブロック図である。図は増幅器と減衰器から構成され，増幅器の電圧増幅度は\( \ A \ \)倍，減衰器の減衰率は\( \ H \ (≦1) \ \)倍である。

出力電圧\( \ v_{\mathrm {out}} \ \)は増幅器の入力電圧\( \ v_{\mathrm {i}} \ \)を用いて\( \ v_{\mathrm {out}}=Av_{\mathrm {i}} \ \)と表せる。一方，\( \ v_{\mathrm {i}} \ \)は\( \ v_{\mathrm {i}}=v_{\mathrm {in}}-Hv_{\mathrm {out}} \ \)であるから，負帰還増幅回路全体の電圧増幅度\( \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} \ \)は，
\[
\begin{eqnarray}
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} &=& \ \fbox {　 （１） 　} \ \\[ 5pt ] \end{eqnarray}
\] となる。ここで\( \ \left| AH\right| \ \)が\( \ 1 \ \)より十分大きいとすると\( \ \fbox {　 （１） 　} \ \)は\( \ \fbox {　 （２） 　} \ \)に近似できる。このことから負帰還増幅回路は電圧増幅度が\( \ \fbox {　 （３） 　} \ \)性質を有することが分かる。

次に，増幅器の電圧増幅度は，
\[
\begin{eqnarray}
A &=&\frac {A_{0}}{\displaystyle 1+\mathrm {j}\frac {f}{f_{\mathrm {c}}}}　・・・・・・・・・・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] で表される周波数特性を有するとする。ここで\( \ A_{0} \ \)と\( \ f_{\mathrm {c}} \ \)はそれぞれ増幅器の直流における電圧増幅度と遮断周波数であり，ともに正の実数である。負帰還増幅回路全体の電圧増幅度\( \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} \ \)は，①式を\( \ \fbox {　 （１） 　} \ \)の\( \ A \ \)に代入し，①式と同じ形に整理することにより
\[
\begin{eqnarray}
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} &=& \ \fbox {　 （４） 　} \ \\[ 5pt ] \end{eqnarray}
\] となる。\( \ \fbox {　 （４） 　} \ \)より，負帰還増幅回路の直流における電圧増幅度は\( \ \displaystyle \frac {A_{\mathrm {0}}}{ \ \fbox {　 （５） 　} \ } \ \)となり，遮断周波数は増幅器の遮断周波数 \( \ f_{\mathrm {c}} \ \)の\( \ \fbox {　 （５） 　} \ \)倍となることがわかる。

〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\left( 1+A_{0}H\right) A_{0}}{\displaystyle 1+\mathrm {j}\frac {f}{\left( 1+A_{0}H\right) f_{\mathrm {c}}}}　　　　　　　&（ロ）&　\frac {\displaystyle \frac {A_{0}}{1+A_{0}H}}{\displaystyle 1+\mathrm {j}\frac {f}{\left( 1+A_{0}H\right) f_{\mathrm {c}}}}　　　　　　　&（ハ）&　\frac {\displaystyle \frac {A_{0}}{1-A_{0}H}}{\displaystyle 1+\mathrm {j}\frac {f}{\left( 1-A_{0}H\right) f_{\mathrm {c}}}} \\[ 5pt ] &（ニ）&　A　　　　　&（ホ）&　H　　　　　&（ヘ）&　AH \\[ 5pt ] &（ト）&　\frac {1}{A}　　　　　&（チ）&　\frac {1}{H}　　　　　&（リ）&　\frac {1}{AH} \\[ 5pt ] &（ヌ）&　1+A_{0}H　　　　　&（ル）&　1-A_{0}H　　　　　&（ヲ）&　\frac {A}{1+AH} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&（ワ）&　A \ の変動の影響を受けにくい \\[ 5pt ] &（カ）&　H \ の変動の影響を受けにくい \\[ 5pt ] &（ヨ）&　A \ と \ H \ の変動の影響を受けにくい \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

負帰還増幅回路に関する問題です。
(4)の変形に苦戦する受験生が多かったと予想されます。(3)まで正答していれば合格圏内にはなるため必須ではありませんが，電験の一次試験では解答群を見ながら，ゴールを見据えて式変形していく能力も必要です。ぜひ練習として取り組んでみて下さい。

1.負帰還増幅回路の電圧増幅率
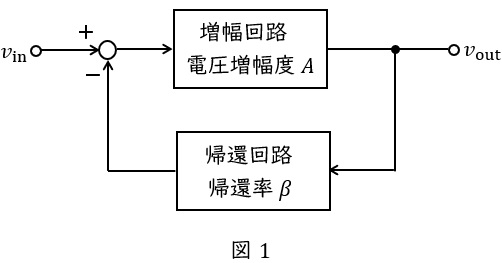
図1において，出力電圧\( \ v_{\mathrm {out}} \ \)を帰還回路で\( \ \beta \ \)倍したものを入力電圧\( \ v_{\mathrm {in}} \ \)から差し引き，さらにそれを増幅回路で\( \ A \ \)倍したものが出力電圧\( \ v_{\mathrm {out}} \ \)となるので，
\[
\begin{eqnarray}
\left( v_{\mathrm {in}}-\beta v_{\mathrm {out}} \right) A&=&v_{\mathrm {out}} \\[ 5pt ] \end{eqnarray}
\] となります。上式を整理すると，全体の増幅率\( \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} \ \)は，
\[
\begin{eqnarray}
Av_{\mathrm {in}}-A\beta v_{\mathrm {out}} &=&v_{\mathrm {out}} \\[ 5pt ] v_{\mathrm {out}}+A\beta v_{\mathrm {out}} &=&Av_{\mathrm {in}} \\[ 5pt ] \left( 1+A\beta \right) v_{\mathrm {out}} &=&Av_{\mathrm {in}} \\[ 5pt ] \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}&=&\frac {A}{1+A\beta } \\[ 5pt ] \end{eqnarray}
\] と求められます。さらに，\( \ A≫1 \ \)であるとすると，
\[
\begin{eqnarray}
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}&=&\frac {A}{1+A\beta } \\[ 5pt ] &=&\frac {1}{\displaystyle \frac {1}{A}+\beta } \\[ 5pt ] &≃&\frac {1}{\beta } \\[ 5pt ] \end{eqnarray}
\] となります。

2.負帰還増幅回路を導入する効果
負帰還増幅回路を導入することにより以下のような効果があります。
①増幅回路\( \ A \ \)が大きい場合，増幅回路の利得を帰還率\( \ \beta \ \)のみでコントロールすることが可能
②電源電圧の変動に対して安定的となる
③増幅回路で発生するひずみや外乱が抑制される
④増幅回路の利得が一定となる帯域幅が大きくなる

【解答】

(1)解答：ヲ
ワンポイント解説「1.負帰還増幅回路の電圧増幅率」と同様に考えると，
\[
\begin{eqnarray}
v_{\mathrm {out}}&=&A\left( v_{\mathrm {in}}-H v_{\mathrm {out}} \right) \\[ 5pt ] &=&A v_{\mathrm {in}}-AH v_{\mathrm {out}} \\[ 5pt ] v_{\mathrm {out}}+AH v_{\mathrm {out}}&=&A v_{\mathrm {in}} \\[ 5pt ] \left( 1+AH \right) v_{\mathrm {out}}&=&A v_{\mathrm {in}} \\[ 5pt ] \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}&=&\frac {A}{1+AH} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：チ
(1)解答式において，\( \ \left| AH\right| \ \)が\( \ 1 \ \)より十分大きいとすると，
\[
\begin{eqnarray}
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}&=&\frac {A}{1+AH} \\[ 5pt ] &≃&\frac {A}{AH} \\[ 5pt ] &=&\frac {1}{H} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ワ
(2)解答式より，負帰還増幅回路は電圧増幅度が\( \ A \ \)の変動の影響を受けにくいことがわかる。

(4)解答：ロ
①を(1)の解答式の\( \ A \ \)に代入すると，
\[
\begin{eqnarray}
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}&=&\frac {A}{1+AH} \\[ 5pt ] &=&\frac {\displaystyle \frac {A_{0}}{\displaystyle 1+\mathrm {j}\frac {f}{f_{\mathrm {c}}}}}{\displaystyle 1+\frac {A_{0}}{\displaystyle 1+\mathrm {j}\frac {f}{f_{\mathrm {c}}}}H} \\[ 5pt ] &=&\frac {\displaystyle \frac {A_{0}}{\displaystyle 1+\mathrm {j}\frac {f}{f_{\mathrm {c}}}}}{\displaystyle \frac {\displaystyle 1+\mathrm {j}\frac {f}{f_{\mathrm {c}}}+A_{0}H}{\displaystyle 1+\mathrm {j}\frac {f}{f_{\mathrm {c}}}}} \\[ 5pt ] &=&\frac {A_{0}}{\displaystyle 1+A_{0}H+\mathrm {j}\frac {f}{f_{\mathrm {c}}}} \\[ 5pt ] &=&\frac {\displaystyle \frac {A_{0}}{1+A_{0}H}}{\displaystyle \frac {\displaystyle 1+A_{0}H+\mathrm {j}\frac {f}{f_{\mathrm {c}}}}{1+A_{0}H}} \\[ 5pt ] &=&\frac {\displaystyle \frac {A_{0}}{1+A_{0}H}}{\displaystyle 1+\mathrm {j}\frac {f}{\left( 1+A_{0}H\right) f_{\mathrm {c}}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヌ
直流における電圧増幅度は，(4)解答式に\( \ f=0 \ \)を代入すると，
\[
\begin{eqnarray}
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}&=&\frac {\displaystyle \frac {A_{0}}{1+A_{0}H}}{\displaystyle 1+\mathrm {j}\frac {0}{\left( 1+A_{0}H\right) f_{\mathrm {c}}}} \\[ 5pt ] &=&\frac {A_{0}}{1+A_{0}H} \\[ 5pt ] \end{eqnarray}
\] と求められる。