Contents
【問題】
【難易度】★★★☆☆(普通)
汽力発電所において,定格容量\( \ 5 \ 000 \ \mathrm {[kV\cdot A]} \ \)の発電機が\( \ 9 \ \)時から\( \ 22 \ \)時の間に下表に示すような運転を行ったとき,発熱量\( \ 44 \ 000 \ \mathrm {[kJ/kg]} \ \)の重油を\( \ 14 \ \mathrm {[t]} \ \)消費した。この\( \ 9 \ \)時から\( \ 22 \ \)時の間の運転について,次の(a)及び(b)に答えよ。
ただし,所内率は\( \ 5 \ \mathrm {[%]} \ \)とする。
発電機の運転状態
\[
\begin{array}{|c|c|c|}
\hline
時 刻 & 皮相電力 \ \mathrm {[kV\cdot A]} & 力率 \ \mathrm {[%]} \\
\hline
9 \ 時 \ ~ \ 13 \ 時 & 4 \ 500 & 遅れ \ 85 \\
\hline
13 \ 時 \ ~ \ 18 \ 時 & 5 \ 000 & 遅れ \ 90 \\
\hline
18 \ 時 \ ~ \ 22 \ 時 & 4 \ 000 & 進み \ 95 \\
\hline
\end{array}
\]
(a) 発電端の発電電力量\( \ \mathrm {[MW\cdot h]} \ \)として,正しいのは次のうちどれか。
(1) \( \ 12 \ \) (2) \( \ 23 \ \) (3) \( \ 38 \ \) (4) \( \ 53 \ \) (5) \( \ 59 \ \)
(b) 送電端熱効率\( \ \mathrm {[%]} \ \)の値として最も近いのは次のうちどれか
(1) \( \ 28.8 \ \) (2) \( \ 29.4 \ \) (3) \( \ 31.0 \ \) (4) \( \ 31.6 \ \) (5) \( \ 32.2 \ \)
【ワンポイント解説】
与えられた条件から汽力発電所の発電電力量と送電端熱効率を求める問題です。
(a)の表で不要な情報である遅れや進みがあること,(b)の問題が送電端熱効率であること,等が受験生を惑わす問題です。途中計算を丁寧に行い,計算間違いのないよう十分注意して解いて下さい。
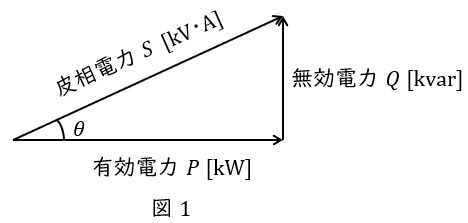
1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \),リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び,図1のようにベクトル図を描きます。さらに,有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ,
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。図1において,力率は\( \ \cos \theta \ \)で定義され,
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ]
\end{eqnarray}
\]
となります。
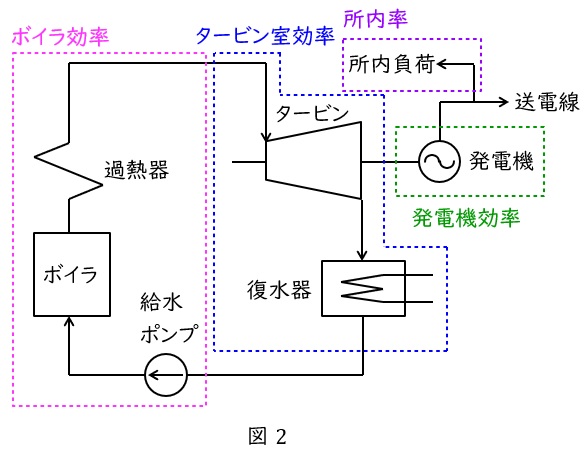
2.汽力発電所の各効率
汽力発電所で用いられる効率は以下の通りです。計算簡略化の為,すべて小数表記での計算となっています。効率の低下は燃料の使用量(支出)に影響するため,電力会社では熱効率が非常に重要なファクターとなっています。
①ボイラ効率\( \ \eta _{\mathrm {B}} \ \)
ボイラで燃料を燃焼し,給水を蒸気にする際の熱交換率の指標です。排ガス損失等があります。
\[
\begin{eqnarray}
\eta _{\mathrm {B}}&=&\frac {ボイラの蒸気として得た熱量}{燃料使用量から換算した熱量} \\[ 5pt ]
\end{eqnarray}
\]
②タービン室効率\( \ \eta _{\mathrm {T}} \ \)
タービンに入った蒸気がどの程度のタービン出力になるかの効率で,タービン室という名前はタービンと復水器を合わせた効率という意味です。一般的な汽力発電所では一番ロスが大きい場所となります。
\[
\begin{eqnarray}
\eta _{\mathrm {T}}&=&\frac {タービン軸出力}{タービンへ入る蒸気の熱量} \\[ 5pt ]
\end{eqnarray}
\]
③発電機効率\( \ \eta _{\mathrm {G}} \ \)
発電機の風損や巻線抵抗損等を考慮した効率で,一般的な水素発電機では\( \ \mathrm {98~99%} \ \)程度となっています。
\[
\begin{eqnarray}
\eta _{\mathrm {G}}&=&\frac {発電機出力}{タービン軸出力} \\[ 5pt ]
\end{eqnarray}
\]
④発電端効率\( \ \eta _{\mathrm {P}} \ \)
発電ユニットの効率を表すもので,燃料の熱量がどの程度発電されたかを示す指標です。
\[
\begin{eqnarray}
\eta _{\mathrm {P}}&=&\frac {発電機出力}{燃料使用量から換算した熱量}&=&\eta _{\mathrm {B}}\cdot \eta _{\mathrm {T}}\cdot \eta _{\mathrm {G}} \\[ 5pt ]
\end{eqnarray}
\]
⑤送電端効率\( \ \eta _{\mathrm {S}} \ \)
発電端効率から所内率\( \ L \ \)を考慮し算出した効率で,発電所としての総合効率の指標となります。
\[
\begin{eqnarray}
\eta _{\mathrm {S}}&=&\eta _{\mathrm {P}}( 1-L ) \\[ 5pt ]
\end{eqnarray}
\]
3.\( \ \mathrm {[kJ]} \ \)と\( \ \mathrm {[kW\cdot h]} \ \)の変換
単位の定義より,
\[
\begin{eqnarray}
1 \ \mathrm {[kJ/s]} &=&1 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,両辺の単位に\( \ \mathrm {[s]} \ \)をかけると,
\[
\begin{eqnarray}
1 \ \mathrm {[kJ]} &=&1 \ \mathrm {[kW\cdot s]} \\[ 5pt ]
\end{eqnarray}
\]
となり,両辺に\( \ 1 \ \mathrm {[h]}=3 \ 600 \ \mathrm {[s]} \ \)を考慮して,\( \ 3600 \ \)をかけると,
\[
\begin{eqnarray}
3 \ 600 \ \mathrm {[kJ]} &=&1 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(4)
\( \ 9 \ \)時~\( \ 13 \ \)時,\( \ 13 \ \)時~\( \ 18 \ \)時,\( \ 18 \ \)時~\( \ 22 \ \)時の発電電力をそれぞれ\( \ P_{1} \ \mathrm {[kW]} \ \),\( \ P_{2} \ \mathrm {[kW]} \ \),\( \ P_{3} \ \mathrm {[kW]} \ \)とすると,ワンポイント解説「1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り,
\[
\begin{eqnarray}
P_{1} &=&4 \ 500 \times 0.85 \\[ 5pt ]
&=&3 \ 825 \ \mathrm {[kW]} \\[ 5pt ]
P_{2} &=&5 \ 000 \times 0.90 \\[ 5pt ]
&=&4 \ 500 \ \mathrm {[kW]} \\[ 5pt ]
P_{3} &=&4 \ 000 \times 0.95 \\[ 5pt ]
&=&3 \ 800 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,発電電力量\( \ W_{\mathrm {G}} \ \mathrm {[MW\cdot h]} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {G}} &=&P_{1}\times \left( 13-9\right) +P_{2}\times \left( 18-13\right) +P_{3}\times \left( 22-18\right) \\[ 5pt ]
&=&3 \ 825\times 4 +4 \ 500\times 5 +3 \ 800\times 4 \\[ 5pt ]
&=&53 \ 000 \ \mathrm {[kW\cdot h]} → 53 \ \mathrm {[MW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(2)
所内率\( \ L=0.05 \ \)であるから,送電電力量\( \ W_{\mathrm {S}} \ \mathrm {[kW\cdot h]} \ \)は,ワンポイント解説「2.汽力発電所の各効率」の通り,
\[
\begin{eqnarray}
W_{\mathrm {S}} &=&\left( 1-L\right) W_{\mathrm {G}} \\[ 5pt ]
&=&\left( 1-0.05\right) \times 53 \ 000 \\[ 5pt ]
&=&50 \ 350 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,熱量換算した値\( \ Q_{\mathrm {S}} \ \mathrm {[kJ]} \ \)は,ワンポイント解説「3.\( \ \mathrm {[kJ]} \ \)と\( \ \mathrm {[kW\cdot h]} \ \)の変換」の通り,
\[
\begin{eqnarray}
Q_{\mathrm {S}} &=&3 \ 600W_{\mathrm {S}} \\[ 5pt ]
&=&3 \ 600\times 50 \ 350 \\[ 5pt ]
&=&181 \ 260 \ 000 \ \mathrm {[kJ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,今回使用した重油の発熱量\( \ Q_{\mathrm {i}} \ \mathrm {[kJ]} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {i}} &=&44 \ 000\times 14\times 10^{3} \\[ 5pt ]
&=&616 \ 000 \ 000 \ \mathrm {[kJ]} \\[ 5pt ]
\end{eqnarray}
\]
であるので,送電端熱効率\( \ \eta _{\mathrm {S}} \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
\eta _{\mathrm {S}} &=&\frac {Q_{\mathrm {S}}}{Q_{\mathrm {i}}}\times 100 \\[ 5pt ]
&=&\frac {181 \ 260 \ 000}{616 \ 000 \ 000}\times 100 \\[ 5pt ]
&=&29.4 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは