《電力》〈火力〉[H18:問15]汽力発電所の復水器での損失とタービン室効率に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

復水器での冷却に海水を使用する汽力発電所が出力\( \ 600 \ \mathrm {[MW]} \ \)で運転しており，復水器冷却水量が\( \ 24 \ \mathrm {[m^{3} / s]} \ \)，冷却水の温度上昇が\( \ 7 \ \mathrm {[{}^{\circ }C]} \ \)であるとき，次の\( \ \mathrm {(a)} \ \)及び\( \ \mathrm {(b)} \ \)に答えよ。

ただし，海水の比熱を\( \ 4.02 \ \mathrm {[kJ / (kg\cdot K)]} \ \)，密度を\( \ 1.02\times 10^{3} \ \mathrm {[kg/m^{3}]} \ \)，発電機効率を\( \ 98 \ \mathrm {[％]} \ \)とする。

\( \ \mathrm {(a)} \ \)　復水器で海水へ放出される熱量\( \ \mathrm {[kJ / s]} \ \)の値として，最も近いのは次のうちどれか。

　　(1)　\( \ 4.25\times 10^{4} \ \)　　(2)　\( \ 1.71\times 10^{5} \ \)　　(3)　\( \ 6.62\times 10^{5} \ \)
　　(4)　\( \ 6.89\times 10^{5} \ \)　　(5)　\( \ 8.61\times 10^{5} \ \)

\( \ \mathrm {(b)} \ \)　タービン室効率\( \ \mathrm {[％]} \ \)の値として，最も近いのは次のうちどれか。ただし，条件を示していない損失は無視できるものとする。

　(1)　\( \ 41.5 \ \)　　(2)　\( \ 46.5 \ \)　　(3)　\( \ 47.0 \ \)　　(4)　\( \ 47.5 \ \)　　(5)　 \( \ 48.0 \ \)

【ワンポイント解説】

汽力発電所の復水器での損失とタービン室効率に関する問題です。
熱力学の要素が多い問題で，得意不得意が大きく分かれる問題です。
電気系ではあまり学習しない内容ですがイメージがしやすい内容なので，過去問を通して理解していくようにしましょう。

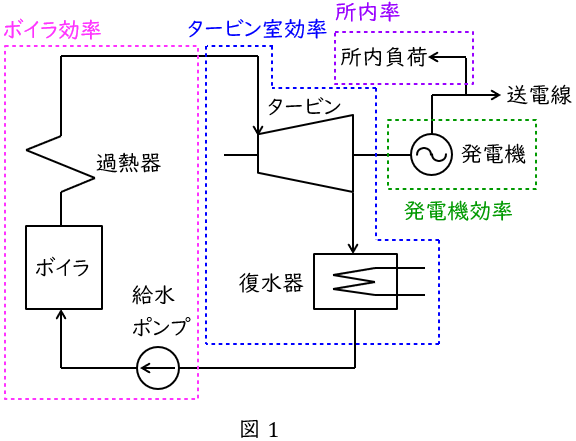
1.汽力発電所の各効率
汽力発電所で用いられる効率は以下の通りです。計算簡略化の為，すべて小数表記での計算となっています。効率の低下は燃料の使用量（支出）に影響するため，電力会社では熱効率が非常に重要なファクターとなっています。

①ボイラ効率\( \ \eta _{\mathrm {B}} \ \)
ボイラで燃料を燃焼し，給水を蒸気にする際の熱交換率の指標です。排ガス損失等があります。
\[
\begin{eqnarray}
\eta _{\mathrm {B}}&=&\frac {ボイラの蒸気として得た熱量}{燃料使用量から換算した熱量} \\[ 5pt ] \end{eqnarray}
\]

②タービン室効率\( \ \eta _{\mathrm {T}} \ \)
タービンに入った蒸気がどの程度のタービン出力になるかの効率で，タービン室という名前はタービンと復水器を合わせた効率という意味です。一般的な汽力発電所では一番ロスが大きい場所となります。
\[
\begin{eqnarray}
\eta _{\mathrm {T}}&=&\frac {タービン軸出力}{タービンへ入る蒸気の熱量} \\[ 5pt ] \end{eqnarray}
\]

③発電機効率\( \ \eta _{\mathrm {G}} \ \)
発電機の風損や巻線抵抗損等を考慮した効率で，一般的な水素発電機では\( \ \mathrm {98～99％} \ \)程度となっています。
\[
\begin{eqnarray}
\eta _{\mathrm {G}}&=&\frac {発電機出力}{タービン軸出力} \\[ 5pt ] \end{eqnarray}
\]

④発電端効率\( \ \eta _{\mathrm {P}} \ \)
発電ユニットの効率を表すもので，燃料の熱量がどの程度発電されたかを示す指標です。
\[
\begin{eqnarray}
\eta _{\mathrm {P}}&=&\frac {発電機出力}{燃料使用量から換算した熱量}&=&\eta _{\mathrm {B}}\cdot \eta _{\mathrm {T}}\cdot \eta _{\mathrm {G}} \\[ 5pt ] \end{eqnarray}
\]

⑤送電端効率\( \ \eta _{\mathrm {S}} \ \)
発電端効率から所内率\( \ L \ \)を考慮し算出した効率で，発電所としての総合効率の指標となります。
\[
\begin{eqnarray}
\eta _{\mathrm {S}}&=&\eta _{\mathrm {P}}( 1-L ) \\[ 5pt ] \end{eqnarray}
\]

2.\( \ \mathrm {[kJ]} \ \)と\( \ \mathrm {[kW\cdot h]} \ \)の変換
単位の定義より，
\[
\begin{eqnarray}
1 \ \mathrm {[kJ / s]} &=&1 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] であるから，両辺の単位に\( \ \mathrm {[s]} \ \)をかけると，
\[
\begin{eqnarray}
1 \ \mathrm {[kJ]} &=&1 \ \mathrm {[kW\cdot s]} \\[ 5pt ] \end{eqnarray}
\] となり，両辺に\( \ 1 \ \mathrm {[h]}=3 \ 600 \ \mathrm {[s]} \ \)を考慮して，\( \ 3 \ 600 \ \)をかけると，
\[
\begin{eqnarray}
3 \ 600 \ \mathrm {[kJ]} &=&1 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] となります。

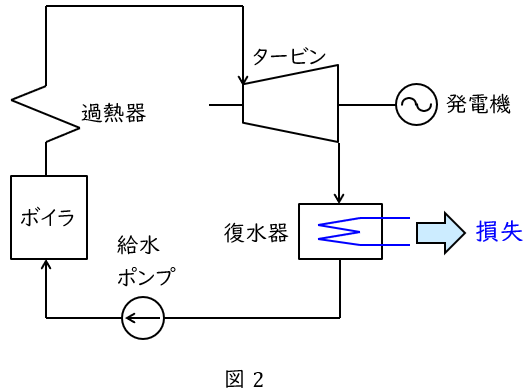
3.海水の温度上昇\( \ \Delta T \ \)と熱量\( \ Q \ \)の関係
海水の流量を\( \ W \ \mathrm {[m^{3} / s]} \ \)，海水の比熱容量を\( \ C \ \mathrm {[kJ / \left( kg\cdot K\right) ]} \ \)，海水の密度を\( \ \rho \ \mathrm {[kg / m^{3}]} \ \)，温度上昇を\( \ \Delta T \ \mathrm {[{}^{\circ }C]} \ \)とすると，\( \ 1 \ \mathrm {[s]} \ \)当たりに持ち去る熱量\( \ Q \ \mathrm {[kJ / s]} \ \)は，
\[
\begin{eqnarray}
Q &=&C\rho W\Delta T \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(a)解答：(4)
復水器冷却水量\( \ W=24 \ \mathrm {[m^{3} / s]} \ \)，冷却水の温度上昇\( \ \Delta T=7 \ \mathrm {[{}^{\circ }C]} \ \)，海水の比熱を\( \ C=4.02 \ \mathrm {[kJ / (kg\cdot K)]} \ \)，密度\( \ \rho =1.02\times 10^{3} \ \mathrm {[kg/m^{3}]} \ \)なので，復水器で海水へ放出される熱量\( \ Q_{w} \ \mathrm {[kJ / s]} \ \)は，ワンポイント解説「3.海水の温度上昇\( \ \Delta T \ \)と熱量\( \ Q \ \)の関係」の通り，
\[
\begin{eqnarray}
Q_{w} &=&C\rho W\Delta T \\[ 5pt ] &=&4.02\times 1.02\times 10^{3} \times 24 \times 7 \\[ 5pt ] &≒&6.889\times 10^{5}　→　6.89\times 10^{5} \ \mathrm {[kJ / s]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
汽力発電所の出力\( \ P_{G}=600 \ \mathrm {[MW]} \ \)，発電機効率\( \ \eta _{G}=0.98 \ \)なので，タービン軸出力\( \ P_{T} \ \mathrm {[MW]} \ \)は，
\[
\begin{eqnarray}
P_{T} &=&\frac {P_{G}}{\eta _{G}} \\[ 5pt ] &=&\frac {600}{0.98} \\[ 5pt ] &≒&612.2 \ \mathrm {[MW]} \\[ 5pt ] \end{eqnarray}
\] となり，ワンポイント解説「2.\( \ \mathrm {[kJ]} \ \)と\( \ \mathrm {[kW\cdot h]} \ \)の変換」の通り，\( \ 1 \ \mathrm {[kJ / s]} = 1 \ \mathrm {[kW]} \ \)なので，タービンの軸出力の熱量換算\( \ Q_{T} \ \mathrm {[kJ / s]} \ \)は，
\[
\begin{eqnarray}
Q_{T} &=&P_{T} \\[ 5pt ] &=&612.2\times 10^{3} \\[ 5pt ] &≒&6.122\times 10^{5} \ \mathrm {[kJ / s]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，タービン室効率\( \ \eta _{T} \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
\eta _{T} &=&\frac {Q_{T}}{Q_{T}+Q_{w}}\times 100 \\[ 5pt ] &=&\frac {6.122\times 10^{5}}{6.122\times 10^{5}+6.889\times 10^{5}}\times 100 \\[ 5pt ] &≒&47.1 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。