【問題】
【難易度】★★★☆☆(普通)
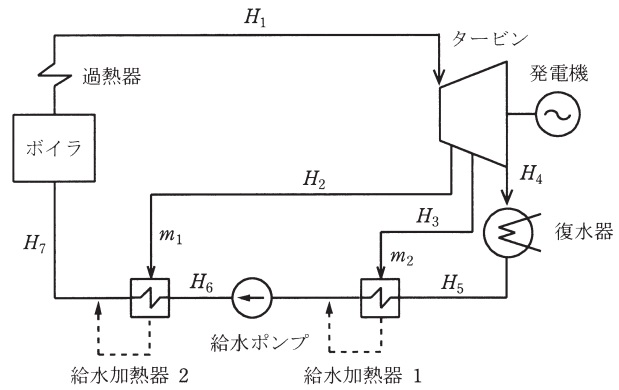
図に示すような再生サイクル汽力発電プラントがある。図中の記号について\( \ H \ \)はエンタルピーを,\( \ m \ \)は抽気量(サイクル流量に対する流量割合)を表すもとのし,添字(数字)は図のとおりとする。また,サイクル流量は\( \ 1 \ \)とし,抽気し給水加熱器で熱交換した後のドレン(蒸気が冷却され復水となった流体)は図の破線に示すようにサイクル中に戻すものとする。なお,給水ポンプの仕事は無視するものとする。
以下の設問にエンタルピー\( \ H_{1} \ \)~\( \ H_{7} \ \)を用いて解答せよ。
(1) タービンからの第\( \ 1 \ \)抽気の抽気量\( \ m_{1} \ \)を表す式を求めよ。
(2) タービンからの第\( \ 2 \ \)抽気の抽気量\( \ m_{2} \ \)を表す式を求めよ。
(3) タービンにおいて,第\( \ 1 \ \)抽気点から第\( \ 2 \ \)抽気点までに得られる仕事\( \ W_{12} \ \)を表す式を求めよ。
(4) サイクルとしての熱効率\( \ \eta \ \)を表す式を求めよ。ただし,記号\( \ m_{1} \ \)及び\( \ m_{2} \ \)を用いてよい。
【ワンポイント解説】
汽力発電所における熱効率の演算をやや応用したような問題です。
慣れてしまえばそれほど難しい内容ではありませんが,初見だと解くのは少し厳しいかもしれません。
給水加熱器における熱交換量が等しいという条件を使用することが本問の肝となります。
【解答】
(1)タービンからの第\( \ 1 \ \)抽気の抽気量\( \ m_{1} \ \)を表す式
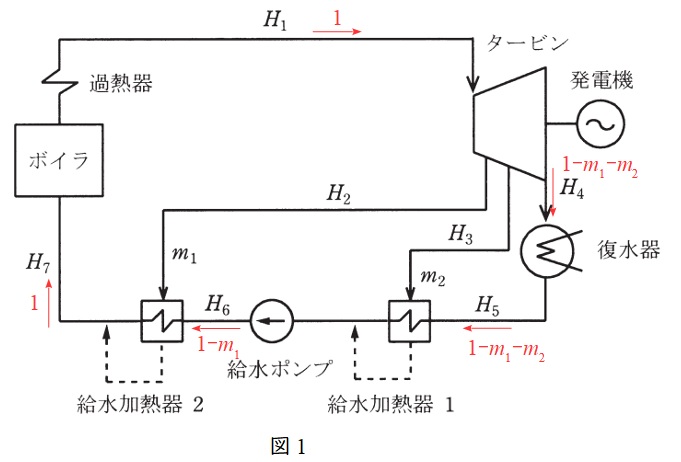
問題図の各エンタルピーにおける蒸気及び給水の流量を示すと図1のようになる。
図1の給水加熱器\( \ 2 \ \)において,抽気が失うエネルギーと給水が得るエネルギーは等しいので,
\[
\begin{eqnarray}
m_{1}\left( H_{2}-H_{7}\right) &=&\left( 1-m_{1}\right) \left( H_{7}-H_{6}\right) \\[ 5pt ]
\end{eqnarray}
\]
が成立する。これを\( \ m_{1} \ \)について整理すると,
\[
\begin{eqnarray}
m_{1}\left( H_{2}-H_{7}\right) &=&\left( H_{7}-H_{6}\right) -m_{1}\left( H_{7}-H_{6}\right) \\[ 5pt ]
m_{1}\left( H_{2}-H_{7}\right) +m_{1}\left( H_{7}-H_{6}\right)&=&H_{7}-H_{6} \\[ 5pt ]
m_{1}\left( H_{2}-H_{7}+H_{7}-H_{6}\right) &=&H_{7}-H_{6} \\[ 5pt ]
m_{1}\left( H_{2}-H_{6}\right) &=&H_{7}-H_{6} \\[ 5pt ]
m_{1}&=&\frac {H_{7}-H_{6}}{H_{2}-H_{6}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)タービンからの第\( \ 2 \ \)抽気の抽気量\( \ m_{2} \ \)を表す式
(1)と同様に,図1の給水加熱器\( \ 1 \ \)において,抽気が失うエネルギーと給水が得るエネルギーは等しいので,
\[
\begin{eqnarray}
m_{2}\left( H_{3}-H_{6}\right) &=&\left( 1-m_{1}-m_{2}\right) \left( H_{6}-H_{5}\right) \\[ 5pt ]
\end{eqnarray}
\]
が成立する。これを\( \ m_{2} \ \)について整理すると,
\[
\begin{eqnarray}
m_{2}\left( H_{3}-H_{6}\right) &=&\left( 1-m_{1}\right) \left( H_{6}-H_{5}\right) -m_{2}\left( H_{6}-H_{5}\right) \\[ 5pt ]
m_{2}\left( H_{3}-H_{6}\right) +m_{2}\left( H_{6}-H_{5}\right) &=&\left( 1-m_{1}\right) \left( H_{6}-H_{5}\right) \\[ 5pt ]
m_{2}\left( H_{3}-H_{6}+H_{6}-H_{5}\right) &=&\left( 1-m_{1}\right) \left( H_{6}-H_{5}\right) \\[ 5pt ]
m_{2}\left( H_{3}-H_{5}\right) &=&\left( 1-m_{1}\right) \left( H_{6}-H_{5}\right) \\[ 5pt ]
m_{2}&=&\left( 1-m_{1}\right) \frac {H_{6}-H_{5}}{H_{3}-H_{5}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,(1)解答式を代入しさらに整理すると,
\[
\begin{eqnarray}
m_{2}&=&\left( 1-\frac {H_{7}-H_{6}}{H_{2}-H_{6}}\right) \frac {H_{6}-H_{5}}{H_{3}-H_{5}} \\[ 5pt ]
&=&\left( \frac {H_{2}-H_{6}}{H_{2}-H_{6}}-\frac {H_{7}-H_{6}}{H_{2}-H_{6}}\right) \frac {H_{6}-H_{5}}{H_{3}-H_{5}} \\[ 5pt ]
&=&\frac {H_{2}-H_{7}}{H_{2}-H_{6}}\cdot \frac {H_{6}-H_{5}}{H_{3}-H_{5}} \\[ 5pt ]
&=&\frac {\left( H_{2}-H_{7}\right) \left( H_{6}-H_{5}\right) }{\left( H_{2}-H_{6}\right) \left( H_{3}-H_{5}\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)タービンにおいて,第\( \ 1 \ \)抽気点から第\( \ 2 \ \)抽気点までに得られる仕事\( \ W_{12} \ \)を表す式
タービンの第\( \ 1 \ \)抽気点から第\( \ 2 \ \)抽気点の間を流れる蒸気流量は\( \ 1-m_{1} \ \)であるから,その間に得られる仕事(エネルギー差)\( \ W_{12} \ \)は,
\[
\begin{eqnarray}
W_{12} &=&\left( 1-m_{1}\right) \left( H_{2}-H_{3}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。上式に(1)解答式を代入して整理すると,
\[
\begin{eqnarray}
W_{12} &=&\left( 1-\frac {H_{7}-H_{6}}{H_{2}-H_{6}}\right) \left( H_{2}-H_{3}\right) \\[ 5pt ]
&=&\left( \frac {H_{2}-H_{6}}{H_{2}-H_{6}}-\frac {H_{7}-H_{6}}{H_{2}-H_{6}}\right) \left( H_{2}-H_{3}\right) \\[ 5pt ]
&=&\frac {H_{2}-H_{7}}{H_{2}-H_{6}} \left( H_{2}-H_{3}\right) \\[ 5pt ]
&=&\frac {\left( H_{2}-H_{7}\right) \left( H_{2}-H_{3}\right) }{H_{2}-H_{6}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)サイクルとしての熱効率\( \ \eta \ \)を表す式
(3)と同様にタービン入口から第\( \ 1 \ \)抽気点までに得られる仕事\( \ W_{01} \ \)は,
\[
\begin{eqnarray}
W_{01} &=&1 \cdot \left( H_{1}-H_{2}\right) \\[ 5pt ]
&=&H_{1}-H_{2} \\[ 5pt ]
\end{eqnarray}
\]
であり,第\( \ 2 \ \)抽気点から復水器までに仕事\( \ W_{23} \ \)は,
\[
\begin{eqnarray}
W_{23} &=&\left( 1-m_{1}-m_{2}\right) \left( H_{3}-H_{4}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。また,ボイラで与えられる熱量\( \ W_{\mathrm {i}} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {i}} &=&1 \cdot \left( H_{1}-H_{7}\right) \\[ 5pt ]
&=&H_{1}-H_{7} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,サイクルの熱効率\( \ \eta \ \)は,
\[
\begin{eqnarray}
\eta &=&\frac {W_{01}+W_{12}+W_{23}}{W_{\mathrm {i}}} \\[ 5pt ]
&=&\frac {H_{1}-H_{2}+\left( 1-m_{1}\right) \left( H_{2}-H_{3}\right) +\left( 1-m_{1}-m_{2}\right) \left( H_{3}-H_{4}\right) }{H_{1}-H_{7}} \\[ 5pt ]
&=&\frac {H_{1}-H_{2}+H_{2}-H_{3}-m_{1}\left( H_{2}-H_{3}\right) +H_{3}-H_{4}-m_{1}\left( H_{3}-H_{4}\right) -m_{2}\left( H_{3}-H_{4}\right) }{H_{1}-H_{7}} \\[ 5pt ]
&=&\frac {H_{1}-H_{2}+H_{2}-H_{3}+H_{3}-H_{4}-m_{1}\left( H_{2}-H_{3}+H_{3}-H_{4}\right) -m_{2}\left( H_{3}-H_{4}\right) }{H_{1}-H_{7}} \\[ 5pt ]
&=&\frac {H_{1}-H_{4}-m_{1}\left( H_{2}-H_{4}\right) -m_{2}\left( H_{3}-H_{4}\right) }{H_{1}-H_{7}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん