【問題】
【難易度】★★★☆☆(普通)
次の文章は,水電解に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
電気分解では,電解質に\( \ 2 \ \)本の電極を入れ,直流電流を流して反応を起こす。\( \ 2 \ \)本の電極のうちの陰極では,最も反応しやすい物質が電子を\( \ \fbox { (1) } \ \)反応が起こる。電気分解の中でも,太陽光発電や風力発電を用いた水素製造にも適用されているアルカリ水電解は水酸化カリウム\( \ \left( \mathrm {KOH} \right) \ \)水溶液を電解質とするものである。
[陰極] \( \ \mathrm {2 H_{2}O+2e^{-}→ H_{2}+2OH^{-}} \ \)
[陽極] \( \ \mathrm {\fbox { (2) } \ OH^{-}→O_{2}+2 H_{2}O+ \ \fbox { (2) } \ e^{-}} \ \)
陰極又は陽極で変化する物質の量は,流した電気量に比例することをファラデーの電気分解の法則,電子\( \ 1 \ \mathrm {mol} \ \)のもつ電気量の大きさをファラデー定数:\( \ F \ \)といい,
\[
\begin{eqnarray}
F&=&9.65\times 10^{4} \ \mathrm {C/mol} \\[ 5pt ]
\end{eqnarray}
\]
である。
ここでは,二つの電解セルを直列に接続した電解槽について考える。電流効率\( \ 100 \ % \ \)のときに\( \ 1 \ 000 \ \mathrm {A} \ \)で\( \ 1 \ \)時間通電して得られる水素の量はファラデーの電気分解の法則を用いると\( \ \fbox { (3) } \ \mathrm {mol} \ \)であることがわかる。このとき,同時に発生する酸素の体積は水素の体積の\( \ \fbox { (4) } \ \)倍である。この電解槽の一つの電解セルの電圧が\( \ 1.80 \ \mathrm {V} \ \)で電流効率が\( \ 97 \ % \ \)のとき,上と同じ量の水素を製造するために必要な電気量は\( \ \fbox { (5) } \ \mathrm {kA\cdot h} \ \),電力量は\( \ \fbox { (6) } \ \mathrm {kW\cdot h} \ \)である。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& 4 &(ロ)& \frac {1}{4} &(ハ)& 3 \\[ 5pt ]
&(ニ)& 3.71 &(ホ)& 受け取る還元 &(ヘ)& 1 \\[ 5pt ]
&(ト)& 74.6 &(チ)& 2 &(リ)& 放出する還元 \\[ 5pt ]
&(ヌ)& \frac {1}{2} &(ル)& 18.7 &(ヲ)& 3.49 \\[ 5pt ]
&(ワ)& 受け取る酸化 &(カ)& 37.3 &(ヨ)& 3.60 \\[ 5pt ]
&(タ)& 1.03 &(レ)& 0.97 &(ソ)& 1.85 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
水電解に関する問題です。
水素は燃焼時に\( \ \mathrm {CO_{2}} \ \)を発生しないので近年注目されるエネルギーであること,アルカリ水電解により比較的容易に水素を得られること,等から本問は出題されたと考えられます。
ファラデーの法則や酸化,還元等の内容は二次電池でもそのまま応用できるので,必ず理解しておくようにして下さい。
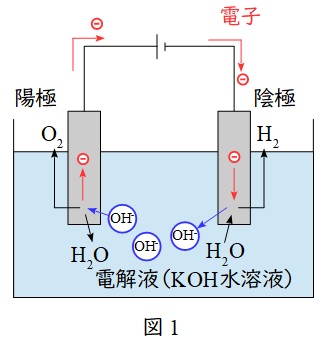
1.水電解
水を電気分解することで,水素と酸素を製造するシステムです。
陽極では電子を放出する酸化反応により酸素が発生し,陰極では電子を受け取る還元反応により水素が発生します。
電解質はアルカリ水溶液である水酸化カリウム\( \ \left( \mathrm {KOH} \right) \ \)水溶液で,反応は吸熱反応となります。
反応式
\[
\begin{eqnarray}
陽極&:& \mathrm {2OH^{-}}&& &→& \mathrm {\frac {1}{2}O_{2}} &+& \mathrm {H_{2}O} &+& \mathrm {2e^{-}} \\[ 5pt ]
陰極&:& \mathrm {2 H_{2}O} &+& \mathrm {2e^{-}} &→& \mathrm {H_{2}} &+& \mathrm {2OH^{-}} \\[ 5pt ]
\hline
全体&:& \mathrm {H_{2}O} && &→& \mathrm {H_{2}} &+& \mathrm {\frac {1}{2}O_{2}} \\[ 5pt ]
\end{eqnarray}
\]
2.ファラデーの電気分解の法則
ファラデーの電気分解の法則には以下の2つの法則があります。
第一法則:電極に析出される量は電気量(電流×時間)に比例する。
第二法則:電極に析出される量は化学当量(原子量÷原子価)に比例する。
※上記内容は,暗記するのではなく,計算問題を繰り返すことで内容を理解するようにしましょう。
【解答】
(1)解答:ホ
題意より解答候補は,(ホ)受け取る還元,(リ)放出する還元,(ワ)受け取る酸化,になると思います。
ワンポイント解説「1.水電解」の通り,陰極での反応は電子を受け取る還元反応となります。そもそも電子を放出する反応を酸化反応,電子を受け取る反応を還元反応というので,(リ)と(ワ)はどのような酸化還元反応においても起こらないということを知っておきましょう。
(2)解答:イ
題意より解答候補は,(イ)\( \ 4 \ \),(ロ)\( \ \displaystyle \frac {1}{4} \ \),(ハ)\( \ 3 \ \),(ヘ)\( \ 1 \ \),(チ)\( \ 2 \ \),(ヌ)\( \ \displaystyle \frac {1}{2} \ \),になると思います。
ワンポイント解説「1.水電解」の通り,陽極での反応は,\( \ \displaystyle \mathrm {2OH^{-}}→\mathrm {\frac {1}{2}O_{2}} + \mathrm {H_{2}O} + \mathrm {2e^{-}} \ \)となりますが,問題においては\( \ \mathrm {O_{2}} \ \)や\( \ \mathrm {H_{2}O} \ \)の係数がすべて\( \ 2 \ \)倍となっているので他の係数も\( \ 2 \ \)倍すると,\( \ \mathrm {4OH^{-}}→\mathrm {O_{2}} + \mathrm {2H_{2}O} + \mathrm {4e^{-}} \ \)となります。
(3)解答:カ
\( \ 1 \ 000 \ \mathrm {A} \ \)で\( \ 1 \ \)時間通電して得られる電気量\( \ Q \ \mathrm {[C]} \ \)は,
\[
\begin{eqnarray}
Q&=&1 \ 000\times 3 \ 600 \\[ 5pt ]
&=&3.6\times 10^{6} \ \mathrm {[C]} \\[ 5pt ]
\end{eqnarray}
\]
であり,ファラデーの電気分解の法則より電子の物質量\( \ M_{\mathrm {e}} \ \mathrm {[mol]} \ \)は,
\[
\begin{eqnarray}
M_{\mathrm {e}}&=&\frac {Q}{F} \\[ 5pt ]
&=&\frac {3.6\times 10^{6}}{96500} \\[ 5pt ]
&≒&37.306 \ \mathrm {[mol]} \\[ 5pt ]
\end{eqnarray}
\]
となる。陰極の反応式より,電子\( \ 2 \ \mathrm {[mol]} \ \)に対し反応する水素は\( \ 1 \ \mathrm {[mol]} \ \)であり,本問おいては二つの電解セルを直列に接続しているので二つ合わせて水素は\( \ 2 \ \mathrm {[mol]} \ \)生成されることになる。したがって,水素の物質量\( \ M_{\mathrm {H}} \ \mathrm {[mol]} \ \)は,
\[
\begin{eqnarray}
M_{\mathrm {H}}&=&M_{\mathrm {e}} \\[ 5pt ]
&≒&37.306 → 37.3 \ \mathrm {[mol]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヌ
題意より解答候補は,(イ)\( \ 4 \ \),(ロ)\( \ \displaystyle \frac {1}{4} \ \),(ハ)\( \ 3 \ \),(ヘ)\( \ 1 \ \),(チ)\( \ 2 \ \),(ヌ)\( \ \displaystyle \frac {1}{2} \ \),になると思います。
ワンポイント解説「1.水電解」の全体の反応式の通り,発生する酸素の物質量は水素の物質量の\( \ \displaystyle \frac {1}{2} \ \)倍であり,気体\( \ 1 \ \mathrm {[mol]} \ \)の標準状態における体積は\( \ 22.4 \ \mathrm {[L]} \ \)で等しいため,発生する酸素の体積は水素の体積の\( \ \displaystyle \frac {1}{2} \ \)倍となります。
(5)解答:タ
題意の条件における電気量を\( \ Q_{\mathrm {x}} \ \mathrm {[kA\cdot h]} \ \)とすると,通電する電気量が(3)の\( \ Q=3.6\times 10^{6} \ \mathrm {[C]} \ \)と等しくなければならないので,
\[
\begin{eqnarray}
Q&=&Q_{\mathrm {x}}\times 1 \ 000 \times 3 \ 600 \times 0.97 \\[ 5pt ]
3.6\times 10^{6}&=&Q_{\mathrm {x}}\times 1 \ 000 \times 3 \ 600 \times 0.97 \\[ 5pt ]
Q_{\mathrm {x}}&=&\frac {3.6\times 10^{6}}{1 \ 000 \times 3 \ 600 \times 0.97} \\[ 5pt ]
&≒&1.0309 → 1.03 \ \mathrm {[kA\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(6)解答:ニ
一つの電解セルの電圧が\( \ V=1.80 \ \mathrm {[V]} \ \)であるため,必要な電力量\( \ W \ \mathrm {[kW\cdot h]} \ \)は,
\[
\begin{eqnarray}
W&=&Q_{\mathrm {x}}\times 2V \\[ 5pt ]
&=&1.0309\times 2\times 1.80 \\[ 5pt ]
&≒&3.71 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん