【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,直流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な式を解答群の中から選びなさい。
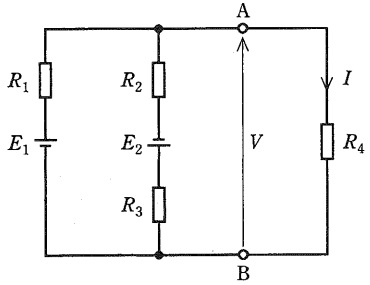
図において,抵抗\( \ R_{4} \ \)に流れる電流\( \ I \ \)をミルマンの定理を用いて求めたい。
まず,電圧源を短絡除去して端子\( \ \mathrm {A – B} \ \)間からみた回路全体のコンダクタンスを求めると\( \ \fbox { (1) } \ \)となる。次に,端子\( \ \mathrm {A – B} \ \)間を短絡したときに,端子\( \ \mathrm {B} \ \)から抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)を介して端子\( \ \mathrm {A} \ \)に流れる電流の和を求め,\( \ \fbox { (1) } \ \)で割れば,\( \ V= \ \fbox { (2) } \ \)となる。したがって,\( \ I= \ \fbox { (3) } \ \)となる。
さらに,\( \ R_{4} \ \)で消費される電力が最大となる\( \ R_{4} \ \)の値を求めてみよう。\( \ R_{4} \ \)で消費される電力\( \ P \ \)は\( \ P=I^{2}R_{4} \ \)で求められるから,\( \ R_{4} \ \)の値が\( \ R_{4}= \ \fbox { (4) } \ \)の条件を満足する場合に電力は最大となり,最大電力\( \ P_{\mathrm {m}} \ \)は\( \ P_{\mathrm {m}}= \ \fbox { (5) } \ \)となる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {\left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}}{R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) } (ロ) \frac {R_{2}R_{3}}{R_{1}+R_{2}+R_{3}} \\[ 5pt ]
&(ハ)& \frac {R_{1}\left( R_{2}+R_{3}\right) }{R_{1}+R_{2}+R_{3}} (ニ) \frac {\left[ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right] ^{2}}{2\left( R_{1}+R_{2}+R_{3}\right) } \\[ 5pt ]
&(ホ)& \frac {R_{2}R_{3}\left [\left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right] }{R_{4}\left( R_{2}+R_{3}\right) \left( R_{1}R_{2}+R_{1}R_{3}+R_{2}R_{3}\right) +R_{1}R_{2}R_{3}\left( R_{2}+R_{3}\right) } \\[ 5pt ]
&(ヘ)& \frac {1}{R_{1}}+\frac {1}{R_{2}}+\frac {1}{R_{3}}+\frac {1}{R_{4}} \ \ (ト) \frac {1}{R_{1}}+\frac {1}{R_{2}+R_{3}} \\[ 5pt ]
&(チ)& \frac {1}{R_{1}}+\frac {1}{R_{4}}+\frac {1}{R_{2}+R_{3}} (リ) \frac {\left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}}{\left( R_{1}+R_{2}+R_{3}\right) R_{4}} \\[ 5pt ]
&(ヌ)& \frac {\left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}}{R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) }R_{4} \ \ (ル) \frac {\left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}}{R_{1}+R_{2}+R_{3}} \\[ 5pt ]
&(ヲ)& \frac {\left[ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right] ^{2}}{4R_{1}\left( R_{2}+R_{3}\right) \left( R_{1}+R_{2}+R_{3}\right) } \\[ 5pt ]
&(ワ)& \frac {R_{2}R_{3}R_{4}\left [\left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right] }{R_{4}\left( R_{2}+R_{3}\right) \left( R_{1}R_{2}+R_{1}R_{3}+R_{2}R_{3}\right) +R_{1}R_{2}R_{3}\left( R_{2}+R_{3}\right) } \\[ 5pt ]
&(カ)& \frac {R_{2}R_{3}\left [\left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right] ^{2}}{4R_{1}\left( R_{2}+R_{3}\right) ^{2}\left( R_{1}R_{2}+R_{1}R_{3}+R_{2}R_{3}\right) } (ヨ) \frac {R_{1}R_{2}R_{3}}{R_{1}R_{2}+R_{1}R_{3}+R_{2}R_{3}} && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
ミルマンの定理を使用した問題です。
解法はそれほど難しくありませんが,計算量が非常に多いため,\( \ 15 \ \)分での完答はかなり厳しいかもしれません。
(4)の計算を省略できた方が完答できた可能性が高いかと思います。
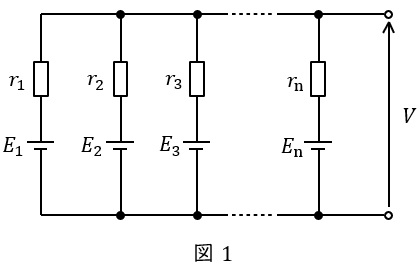
1.ミルマンの定理
図1のような,電源\( \ E_{1},E_{2},\cdots ,E_{\mathrm {n}} \ \)と抵抗\( \ r_{1},r_{2},\cdots ,r_{\mathrm {n}} \ \)が直並列された回路における全体の電圧\( \ V \ \)は,
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {E_{1}}{r_{1}}+\frac {E_{2}}{r_{2}}+\frac {E_{3}}{r_{3}}+\cdots +\frac {E_{\mathrm {n}}}{r_{\mathrm {n}}}}{\displaystyle \frac {1}{r_{1}}+\frac {1}{r_{2}}+\frac {1}{r_{3}}+\cdots +\frac {1}{r_{\mathrm {n}}}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。電源がない時は\( \ E=0 \ \)を代入すれば,ミルマンの定理は成立します。
【解答】
(1)解答:チ
電圧源を短絡除去して端子\( \ \mathrm {A – B} \ \)間からみた回路全体のコンダクタンス\( \ G \ \)は,\( \ R_{1} \ \),\( \ R_{1}+ R_{3} \ \),\( \ R_{4} \ \)の合成コンダクタンスであるから,
\[
\begin{eqnarray}
G&=&\frac {1}{R_{1}}+\frac {1}{R_{4}}+\frac {1}{R_{2}+R_{3}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヌ
電源の向きに注意して問題図の回路にミルマンの定理を適用すると,ワンポイント解説「1.ミルマンの定理」の通り,
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {E_{1}}{R_{1}}+\frac {0}{R_{4}}-\frac {E_{2}}{R_{2}+R_{3}}}{\displaystyle \frac {1}{R_{1}}+\frac {1}{R_{4}}+\frac {1}{R_{2}+R_{3}}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {E_{1}}{R_{1}}-\frac {E_{2}}{R_{2}+R_{3}}}{\displaystyle \frac {1}{R_{1}}+\frac {1}{R_{4}}+\frac {1}{R_{2}+R_{3}}}\times \frac {R_{1}R_{4}\left( R_{2}+R_{3}\right) }{R_{1}R_{4}\left( R_{2}+R_{3}\right) } \\[ 5pt ]
&=&\frac {R_{4}\left( R_{2}+R_{3}\right) E_{1}-R_{1}R_{4}E_{2}}{R_{4}\left( R_{2}+R_{3}\right) +R_{1}\left( R_{2}+R_{3}\right) +R_{1}R_{4}} \\[ 5pt ]
&=&\frac {\left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}}{R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) }R_{4} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:イ
(2)解答式より,電流\( \ I \ \)は,
\[
\begin{eqnarray}
I&=&\frac {V}{R_{4}} \\[ 5pt ]
&=&\frac {\left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}}{R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) }R_{4} \cdot \frac {1}{R_{4}} \\[ 5pt ]
&=&\frac {\left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}}{R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ハ
\( \ R_{4} \ \)で消費される電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&I^{2}R_{4} \\[ 5pt ]
&=&\left\{ \frac {\left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}}{R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) }\right\} ^{2}R_{4} \\[ 5pt ]
&=&\frac {R_{4}\left\{ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right\} ^{2}}{\left\{ R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) \right\} ^{2}} ・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
であり,両辺\( \ R_{4} \ \)で微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}R_{4}}&=&\frac {\left\{ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right\} ^{2}\left\{ R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) \right\} ^{2}-R_{4}\left\{ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right\} ^{2} \left( R_{1}+R_{2}+R_{3}\right) \cdot 2 \left\{ R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) \right\} }{\left\{ R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) \right\} ^{4}} \\[ 5pt ]
&=&\frac {\left\{ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right\} ^{2}\left\{ R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) \right\} }{\left\{ R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) \right\} ^{4}}\left[ \left\{ R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) \right\} -2R_{4}\left( R_{1}+R_{2}+R_{3}\right) \right] \\[ 5pt ]
&=&\frac {\left\{ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right\} ^{2}\left\{ R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) \right\} }{\left\{ R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) \right\} ^{4}}\left\{ R_{1}\left( R_{2}+R_{3}\right) -R_{4}\left( R_{1}+R_{2}+R_{3}\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}R_{4}}=0 \ \)のとき,
\[
\begin{eqnarray}
R_{1}\left( R_{2}+R_{3}\right) -R_{4}\left( R_{1}+R_{2}+R_{3}\right)&=&0 \\[ 5pt ]
R_{1}\left( R_{2}+R_{3}\right) &=&R_{4}\left( R_{1}+R_{2}+R_{3}\right) \\[ 5pt ]
R_{4}&=&\frac {R_{1}\left( R_{2}+R_{3}\right) }{R_{1}+R_{2}+R_{3}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※ 一次試験においては,最大電力となる条件が端子\( \ \mathrm {A – B} \ \)から電源側を見た合成抵抗と\( \ R_{4} \ \)が等しいときと知っていればそれを用いて求めても良いかと思います。
(5)解答:ヲ
(4)解答式を①式に代入すると,
\[
\begin{eqnarray}
P_{\mathrm {m}}&=&\frac {R_{4}\left\{ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right\} ^{2}}{\left\{ R_{1}\left( R_{2}+R_{3}\right) +R_{4}\left( R_{1}+R_{2}+R_{3}\right) \right\} ^{2}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {R_{1}\left( R_{2}+R_{3}\right) }{R_{1}+R_{2}+R_{3}}\left\{ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right\} ^{2}}{\displaystyle \left\{ R_{1}\left( R_{2}+R_{3}\right) +\frac {R_{1}\left( R_{2}+R_{3}\right) }{R_{1}+R_{2}+R_{3}}\left( R_{1}+R_{2}+R_{3}\right) \right\} ^{2}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {R_{1}\left( R_{2}+R_{3}\right) }{R_{1}+R_{2}+R_{3}}\left\{ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right\} ^{2}}{\displaystyle \left\{ R_{1}\left( R_{2}+R_{3}\right) +R_{1}\left( R_{2}+R_{3}\right) \right\} ^{2}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {R_{1}\left( R_{2}+R_{3}\right) }{R_{1}+R_{2}+R_{3}}\left\{ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right\} ^{2}}{\displaystyle 4\left\{ R_{1}\left( R_{2}+R_{3}\right) \right\} ^{2}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {1}{R_{1}+R_{2}+R_{3}}\left\{ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right\} ^{2}}{\displaystyle 4R_{1}\left( R_{2}+R_{3}\right) } \\[ 5pt ]
&=&\frac {\displaystyle \left\{ \left( R_{2}+R_{3}\right) E_{1}-R_{1}E_{2}\right\} ^{2}}{\displaystyle 4R_{1}\left( R_{2}+R_{3}\right) \left( R_{1}+R_{2}+R_{3} \right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん