【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,分布定数回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
図のように,特性インピーダンスがそれぞれ\( \ Z_{1} \ \),\( \ Z_{2} \ \)の2本の無損失線路と抵抗が接続されている。線路間に電気的・磁気的結合はなく,また,\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)それぞれの端子では反射がないものとする。
\( \ \mathrm {A} \ \)端子から接続点\( \ \mathrm {C} \ \)に向かって波頭が階段状で波高値\( \ E \ \)の電圧波が進入したときについて考える。\( \ \mathrm {A} \ \)端子からの入射波による電流\( \ i \ \),接続点\( \ \mathrm {C} \ \)での反射により生じる電圧\( \ E_{1} \ \),電流\( \ i_{1} \ \),それぞれの抵抗に流れる電流\( \ i_{3} \ \),\( \ i_{4} \ \),\( \ Z_{2} \ \)側への透過波による電圧\( \ E_{2} \ \),電流\( \ i_{2} \ \)を図のようにとる。電流は入射波が接続点\( \ \mathrm {C} \ \)に向かって進行する方向及び透過波が接続点\( \ \mathrm {D} \ \)から離れる方向を正とする。
接続点\( \ \mathrm {C} \ \)の電圧,電流の関係はそれぞれ次式で表される。
\[
\begin{eqnarray}
&&E+E_{1}=\fbox { (1) } &・・・・・・・ ①& \\[ 5pt ]
&&i+i_{1}=i_{3}=i_{2}+i_{4} &・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
①式及び②式と,\( \ E_{1}=-Z_{1}i_{1} \ \)であることを考慮すれば,\( \ i_{2}= \ \fbox { (2) } \ \times i_{3} \ \)となる。
ここで,接続点\( \ \mathrm {C} \ \)より\( \ \mathrm {B} \ \)側を見たインピーダンスを\( \ Z \ \)とすると,
\[
\begin{eqnarray}
E+E_{1}=Zi_{3} &・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ i_{1} \ \)を\( \ i \ \),\( \ Z_{1} \ \),\( \ Z \ \)を用いて表すと,
\[
\begin{eqnarray}
i_{1}=\fbox { (3) } \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ E_{2} \ \)は\( \ E \ \),\( \ Z_{1} \ \),\( \ R_{1} \ \),\( \ Z \ \)を用いて,
\[
\begin{eqnarray}
E_{2}=\fbox { (4) } \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ \displaystyle E_{1}=\frac {1}{2}E \ \)となるときの抵抗\( \ R_{1} \ \)を\( \ Z_{1} \ \),\( \ Z_{2} \ \),\( \ R_{2} \ \)を用いて表すと,\( \ R_{1}= \ \fbox { (5) } \ \)となる。
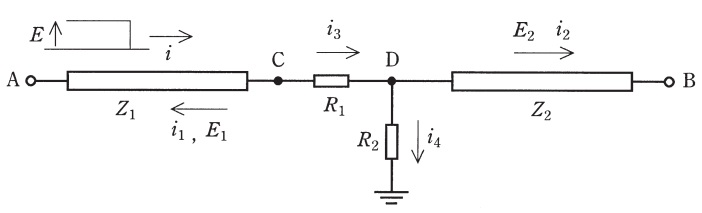
\( \ i_{1} \ \),\( \ E_{1} \ \)は反射波のみとする。
電流は\( \ \mathrm {A→C} \ \),\( \ \mathrm {C→B} \ \),\( \ \mathrm {D→} \ \)接地の向きを正とする。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {2\left( Z_{1}-R_{1}\right) }{Z_{1}-Z}E &(ロ)& \frac {Z_{1}+Z}{Z-Z_{1}}i &(ハ)& R_{1}i_{3}+E_{2} \\[ 5pt ]
&(ニ)& \frac {Z_{2}}{R_{2}+Z_{2}} &(ホ)& \frac {Z_{1}+Z}{Z_{1}-Z}i &(ヘ)& \frac {Z_{1}-Z}{Z_{1}+Z}i \\[ 5pt ]
&(ト)& \frac {R_{2}}{R_{2}+Z_{2}} &(チ)& \frac {1}{3}Z_{1}-\frac {R_{2}Z_{2}}{R_{2}+Z_{2}} &(リ)& \frac {2\left( Z-R_{1}\right) }{Z-Z_{1}}E \\[ 5pt ]
&(ヌ)& E_{2} &(ル)& R_{1}i_{3} &(ヲ)& \frac {2\left( Z-R_{1}\right) }{Z_{1}+Z}E \\[ 5pt ]
&(ワ)& Z_{1}-\frac {R_{2}Z_{2}}{3\left( R_{2}+Z_{2}\right) } &(カ)& \frac {Z_{2}}{R_{1}+Z_{2}} &(ヨ)& 3Z_{1}-\frac {R_{2}Z_{2}}{R_{2}+Z_{2}}
\end{eqnarray}
\]
【ワンポイント解説】
一種受験者であれば,連立方程式を立てることはそれほど難しくはないと思いますが,連立方程式を立ててからの計算が苦労すると思います。連立方程式が解ければ問題ないですが,なかなか解答が導けない場合は問7を選択する決断も考えた方が良いと思います。
【解答】
(1)解答:ハ
接続点\( \ \mathrm {D} \ \)の電圧が\( \ E_{2} \ \),抵抗\( \ R_{1} \ \)を流れる電流が\( \ i_{3} \ \)であるから,
\[
\begin{eqnarray}
E+E_{1}&=&R_{1}i_{3}+E_{2} ・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。
(2)解答:ト
\[
\begin{eqnarray}
E_{2}&=&Z_{2}i_{2}=R_{2}i_{4} \\[ 5pt ]
i_{4}&=&\frac {Z_{2}}{R_{2}}i_{2} \\[ 5pt ]
\end{eqnarray}
\]
であるから,これを②に代入すると,
\[
\begin{eqnarray}
i_{3}&=&i_{2}+i_{4} \\[ 5pt ]
i_{3}&=&i_{2}+\frac {Z_{2}}{R_{2}}i_{2} \\[ 5pt ]
i_{3}&=&\frac {R_{2}+Z_{2}}{R_{2}}i_{2} \\[ 5pt ]
i_{2}&=&\frac {R_{2}}{R_{2}+Z_{2}}i_{3} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヘ
\( \ E=Z_{1}i \ \),\( \ E_{1}=-Z_{1}i_{1} \ \)と②を③に代入すると,
\[
\begin{eqnarray}
E+E_{1}&=&Zi_{3} \\[ 5pt ]
Z_{1}i-Z_{1}i_{1}&=&Z\left( i+i_{1}\right) \\[ 5pt ]
Z_{1}i-Z_{1}i_{1}&=&Zi+Zi_{1} \\[ 5pt ]
i_{1}&=&\frac {Z_{1}-Z}{Z_{1}+Z}i \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヲ
②と(3)解答より,
\[
\begin{eqnarray}
i_{3}&=&i+i_{1} \\[ 5pt ]
&=&i+\frac {Z_{1}-Z}{Z_{1}+Z}i \\[ 5pt ]
&=&\frac {2Z_{1}}{Z_{1}+Z}i \\[ 5pt ]
&=&\frac {2E}{Z_{1}+Z} \\[ 5pt ]
\end{eqnarray}
\]
となる。これと\( \ E+E_{1}=Zi_{3} \ \)を①に代入すると,
\[
\begin{eqnarray}
E_{2}&=&E+E_{1}-R_{1}i_{3} \\[ 5pt ]
&=&Zi_{3}-R_{1}i_{3} \\[ 5pt ]
&=&\left( Z-R_{1}\right) i_{3} \\[ 5pt ]
&=&\left( Z-R_{1}\right) \frac {2E}{Z_{1}+Z} \\[ 5pt ]
&=&\frac {2\left( Z-R_{1}\right) }{Z_{1}+Z}E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヨ
\( \ \displaystyle E_{1}=\frac {1}{2}E \ \),(4)の解答を①に代入すると,
\[
\begin{eqnarray}
E+E_{1}&=&R_{1}i_{3}+E_{2} \\[ 5pt ]
E+\frac {1}{2}E&=&R_{1}\frac {2E}{Z_{1}+Z}+\frac {2\left( Z-R_{1}\right) }{Z_{1}+Z}E \\[ 5pt ]
\frac {3}{2}E&=&\frac {2ZE}{Z_{1}+Z} \\[ 5pt ]
Z&=&3Z_{1} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,題意より,接続点\( \ \mathrm {C} \ \)より\( \ \mathrm {B} \ \)側を見たインピーダンスが\( \ Z \ \)であるから,
\[
\begin{eqnarray}
Z&=&R_{1}+\frac {R_{2}Z_{2}}{R_{2}+Z_{2}} \\[ 5pt ]
R_{1}&=&Z-\frac {R_{2}Z_{2}}{R_{2}+Z_{2}} \\[ 5pt ]
&=&3Z_{1}-\frac {R_{2}Z_{2}}{R_{2}+Z_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん