《理論》〈電子回路〉[H23:問6] マイクロ波真空管に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，クライストロンと呼ばれるマイクロ波真空管に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまるものを解答群の中から選びなさい。

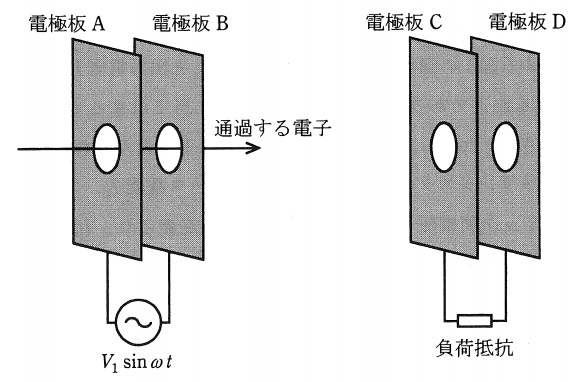
単位電荷を$ \ q \ $，電子の質量を$ \ m \ $とすると，エネルギー$ \ qV_{0} \ $をもって一様な速度で一方向に進む電子ビームの速度は，$ \ \displaystyle v_{0}=\sqrt {\frac {2qV_{0}}{m}} \ $で表される。この電子ビームが，図のように，穴が空いた2枚の電極板$ \ \mathrm {A} \ $，$ \ \mathrm {B} \ $の間を通過する。$ \ 2 \ $枚の電極板$ \ \mathrm {A-B} \ $間に$ \ V_{1}\sin \omega t \ $の交流電圧が印加されているとする。電極板$ \ \mathrm {A-B} \ $間を通過する時間が，交流電圧の周期に対して無視できるほど短いとすると，電子の速度は$ \ 2 \ $枚の電極板を通過した後に$ \ \fbox {　（１）　} \ $となる。したがって，電子ビームが速度変調される。交流電圧の振幅$ \ V_{1} \ $は上記の$ \ V_{0} \ $より十分小さいと仮定し，(注)に示した近似式を用いると，電極板$ \ \mathrm {B} \ $を通過後の電子の速度は$ \ \fbox {　（２）　} \ $となる。ここで，電極板$ \ \mathrm {B} \ $を出たあとも電子が走行を続けるとすると，一番遅い電子に一番速い電子が追いつく集群が起こる。電子同士の反発などは無視すると，一番遅い電子が電極板$ \ \mathrm {B} \ $を出てから次の速い電子がそこを出るまでの時間$ \ \mathit {\Delta }t \ $は$ \ \fbox {　（３）　} \ $である。遅い電子が出てから時間$ \ t \ $が経ったところで最初の集群が起こるとしよう。集群が起こしたところの位置では遅い電子の走行距離と速い電子の走行距離が等しいことから$ \ \fbox {　（４）　} \ $という$ \ \mathit {\Delta }t \ $を用いた関係が導出できる。さらに$ \ \mathit {\Delta }t \ $と$ \ \displaystyle \frac {V_{1}}{V_{0}} \ $の積は微小で無視できるとすると，集群の起こる位置の電極板$ \ \mathrm {B} \ $からの距離は$ \ \fbox {　（３）　} \ $を用いて$ \ \fbox {　（５）　} \ $と近似できる。図のように，集群する位置に穴が空いた$ \ 2 \ $枚の電極板$ \ \mathrm {C} \ $，$ \ \mathrm {D} \ $を置いて，その間に負荷抵抗を挿入し発生する誘導電流を取り出すと，集群して電子密度の濃くなった部分と薄くなった部分が繰り返し通過することから，時間変化する電流が取り出せる。
(注)　　$\displaystyle \sqrt {1+x}≒ 1+\frac {x}{2}$　　　(ただし，$ \ \left| x\right| \ll 1 \ $)

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\sqrt {\frac {2q\left( V_{0}+V_{1}\sin \omega t\right) }{m}}　　　&（ロ）&　\frac {\pi }{2\omega } \\[ 5pt ] &（ハ）&　\frac {\pi }{2\omega }\cdot \frac {V_{0}}{V_{1}}v_{0}　　　&（ニ）&　v_{0}\left( 1+\frac {V_{1}}{2V_{0}}\right) \left( t-\mathit {\Delta } t\right) =v_{0}\left( 1-\frac {V_{1}}{2V_{0}}\right) t \\[ 5pt ] &（ホ）&　v_{0}\left( t-\mathit {\Delta } t\right) =v_{0}\left( 1-\frac {V_{1}}{2V_{0}}\right) t　　　&（ヘ）&　v_{0}\left( 1+\frac {2V_{1}}{V_{0}}\sin \omega t\right) \\[ 5pt ] &（ト）&　\frac {\pi }{\omega }\cdot \frac {V_{0}}{V_{1}}v_{0}　　　&（チ）&　\sqrt {\frac {q\left( V_{0}+V_{1}\sin \omega t\right) }{2m}} \\[ 5pt ] &（リ）&　\sqrt {\frac {q\left( V_{0}+V_{1}\sin \omega t\right) }{m}}　　　&（ヌ）&　\frac {2\pi }{\omega } \\[ 5pt ] &（ル）&　\frac {\pi }{\omega }　　　&（ヲ）&　v_{0}\left( 1+\frac {V_{1}}{2V_{0}}\sin \omega t\right) \\[ 5pt ] &（ワ）&　\frac {2\pi }{\omega }\cdot \frac {V_{0}}{V_{1}}v_{0}　　　&（カ）&　v_{0}\left( 1+\frac {V_{1}}{V_{0}}\sin \omega t\right) \\[ 5pt ] &（ヨ）&　v_{0}\left( 1+\frac {V_{1}}{2V_{0}}\right) \left( t-\mathit {\Delta } t\right) =v_{0}t
\end{eqnarray}
\]

【ワンポイント解説】

クライストロンの原理を計算で求めるような問題です。クライストロンという聞きなれない言葉にビックリしますが、内容は真空電子理論の問題です。
類題の出題率は低いと思われますが，近似計算の慣れも考慮し内容は理解しておきたい問題です。

【解答】

(1)解答：イ
電極板$ \ \mathrm {A-B} \ $通過後のエネルギーは$ \ q\left( V_{0}+V_{1}\sin \omega t\right) \ $となるから，電極板$ \ \mathrm {A-B} \ $通過後の速度$ \ v_{0}^{\prime } \ $は，$V_{0} \ $を$ \ V_{0}+V_{1}\sin \omega t \ $に置き換えて，
\[
\begin{eqnarray}
v_{0}^{\prime }&=&\sqrt {\frac {2q\left( V_{0}+V_{1}\sin \omega t\right) }{m}} \\[ 5pt ] \end{eqnarray}
\] となる。

(2)解答：ヲ
(1)の解答式を変形すると，
\[
\begin{eqnarray}
v_{0}^{\prime }&=&\sqrt {\frac {2q\left( V_{0}+V_{1}\sin \omega t\right) }{m}} \\[ 5pt ] &=&\sqrt {\frac {2qV_{0}}{m}}\sqrt {1+\frac {V_{1}}{V_{0}}\sin \omega t} \\[ 5pt ] &≒& \sqrt {\frac {2qV_{0}}{m}}\left( 1+\frac {V_{1}}{2V_{0}}\sin \omega t\right) \\[ 5pt ] &=&v_{0}\left( 1+\frac {V_{1}}{2V_{0}}\sin \omega t\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ル
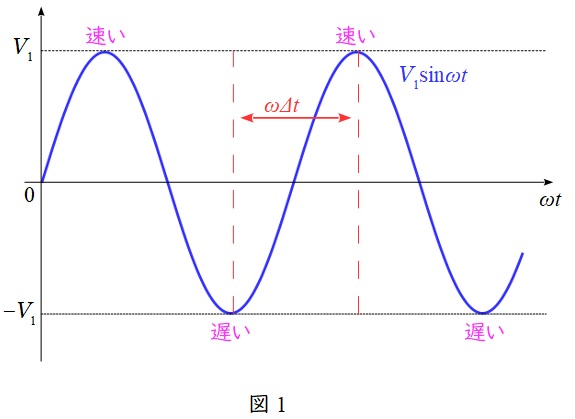
図1に$ \ V_{1}\sin \omega t \ $の波形を示す。図1より，一番遅い電子と一番早い電子の位相差は$ \ \pi \ $であるから，
\[
\begin{eqnarray}
\omega \mathit {\Delta } t&=&\pi \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
\mathit {\Delta } t&=&\frac {\pi }{\omega } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ニ
図1より最も速い電子は$ \ V_{1} \ $，最も遅い電子は$ \ -V_{1} \ $が印加された電子である。それぞれの速度$ \ v_{0\max}^{\prime } \ $及び$ \ v_{0\min}^{\prime } \ $は，(2)解答式に代入すると，
\[
\begin{eqnarray}
v_{0\max}^{\prime }&=&v_{0}\left( 1+\frac {V_{1}}{2V_{0}}\right) \\[ 5pt ] v_{0\min}^{\prime }&=&v_{0}\left( 1-\frac {V_{1}}{2V_{0}}\right) \\[ 5pt ] \end{eqnarray}
\] となる。集群が起こしたところでは，一番遅い電子の移動時間を$ \ t \ $とした時，一番速い電子の移動時間は$ \ t-\mathit {\Delta } t \ $となり，それぞれの移動距離が等しいので，
\[
\begin{eqnarray}
v_{0\max}^{\prime }\left( t-\mathit {\Delta } t \right)&=&v_{0\min}^{\prime } t \\[ 5pt ] v_{0}\left( 1+\frac {V_{1}}{2V_{0}}\right)\left( t-\mathit {\Delta } t \right)&=&v_{0}\left( 1-\frac {V_{1}}{2V_{0}}\right)t \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ト
(4)解答式を計算すると，
\[
\begin{eqnarray}
v_{0}\left( 1+\frac {V_{1}}{2V_{0}}\right)\left( t-\mathit {\Delta } t \right)&=&v_{0}\left( 1-\frac {V_{1}}{2V_{0}}\right)t \\[ 5pt ] \left( 1+\frac {V_{1}}{2V_{0}}\right)\left( t-\mathit {\Delta } t \right)&=&\left( 1-\frac {V_{1}}{2V_{0}}\right)t \\[ 5pt ] t-\mathit {\Delta } t+\frac {V_{1}}{2V_{0}}t-\frac {V_{1}}{2V_{0}}\mathit {\Delta } t&=&t-\frac {V_{1}}{2V_{0}}t \\[ 5pt ] t-\mathit {\Delta } t+\frac {V_{1}}{2V_{0}}t&≃&t-\frac {V_{1}}{2V_{0}}t \\[ 5pt ] -\mathit {\Delta } t+\frac {V_{1}}{2V_{0}}t&=&-\frac {V_{1}}{2V_{0}}t \\[ 5pt ] t&=&\frac {V_{0}}{V_{1}}\mathit {\Delta } t \\[ 5pt ] \end{eqnarray}
\] となるので，集群の起こる位置$ \ x \ $は上式を(4)解答式右辺に代入すると，
\[
\begin{eqnarray}
x&=&v_{0}\left( 1-\frac {V_{1}}{2V_{0}}\right)t \\[ 5pt ] &=&v_{0}\left( 1-\frac {V_{1}}{2V_{0}}\right)\frac {V_{0}}{V_{1}}\mathit {\Delta } t \\[ 5pt ] &=&\frac {V_{0}}{V_{1}}v_{0}\left( \mathit {\Delta } t-\frac {V_{1}}{2V_{0}}\mathit {\Delta } t\right) \\[ 5pt ] &≃&\mathit {\Delta } t\frac {V_{0}}{V_{1}}v_{0} \\[ 5pt ] &=&\frac {\pi }{\omega }\cdot \frac {V_{0}}{V_{1}}v_{0} \\[ 5pt ] \end{eqnarray}
\] と求められる。