【問題】
【難易度】★★☆☆☆(やや易しい)
変圧器の三相結線に関して,次の問に答えよ。
(1) 単相変圧器\( \ 2 \ \)台を用いて\( \ \mathrm {V} \ \)結線した場合,変圧器の利用率は\( \ \displaystyle \frac {\sqrt {3}}{2} \ \left( = 0.866 \right) \ \)であることを説明せよ。
(2) 定格容量\( \ 100 \ \mathrm {[kV\cdot A]} \ \)の単相変圧器\( \ 3 \ \)台を\( \ \Delta – \Delta \ \)結線して三相平衡負荷に配電しているときに,単相変圧器\( \ 1 \ \)台が故障した。この故障した変圧器を回路から除いて\( \ \mathrm {V} \ \)結線にて配電した場合の最大容量\( \ \mathrm {[kV\cdot A]} \ \)を計算せよ。
(3) \( \ 3 \ \)台の同じ容量の単相変圧器を組み合わせた三相変圧器バンクと比較して,一つの鉄心に三相分の巻線を施した三相変圧器の長所と短所を理由を付してそれぞれ一つ以上述べよ。ただし,両者とも三相分の容量は同じとする。
【ワンポイント解説】
変圧器の三相結線である\( \ \mathrm {V} \ \)結線と\( \ \Delta \ \)結線の比較に関する問題です。
本問はあまり時間を要しないため,知識があり選択できれば大きなアドバンテージになったと予想されます。こういう問題を選択できるように準備しましょう。
1.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較
①\( \ \mathrm {\Delta -\Delta } \ \)結線
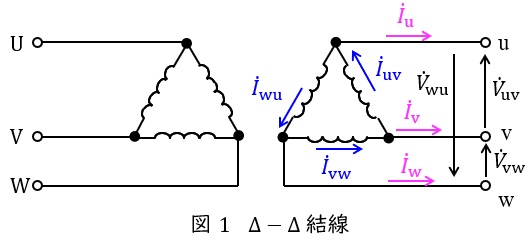
\( \ \mathrm {\Delta -\Delta } \ \)結線の変圧器の回路図とベクトル図を図1及び図2に示します。
図1において,負荷電流\( \ {\dot I}_{\mathrm {u}} \ \mathrm {[A]} \ \)は,変圧器を流れる電流\( \ {\dot I}_{\mathrm {uv}} \ \mathrm {[A]} \ \)及び\( \ {\dot I}_{\mathrm {wu}} \ \mathrm {[A]} \ \)を用いて,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}}&=& {\dot I}_{\mathrm {uv}}-{\dot I}_{\mathrm {wu}} \\[ 5pt ]
\end{eqnarray}
\]
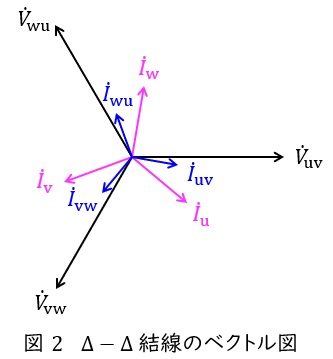
で求められ,ベクトル図上では図2のような関係となり,三相平衡である場合にはそれぞれの大きさの比は,
\[
\begin{eqnarray}
I_{\mathrm {u}}&=& \sqrt {3}I_{\mathrm {uv}} \\[ 5pt ]
\end{eqnarray}
\]
であることが分かります。したがって,各変圧器が分担する容量\( \ S \ \mathrm {[V\cdot A]} \ \)は,負荷の線間電圧を\( \ V_{\mathrm {uv}}=V_{\mathrm {vw}}=V_{\mathrm {wu}}=V \ \),負荷電流を\( \ I_{\mathrm {u}}=I_{\mathrm {v}}=I_{\mathrm {w}}=I \ \)とすると,
\[
\begin{eqnarray}
S&=& \frac {VI}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって,変圧器全体の送電電力\( \ P \ \mathrm {[W]} \ \)は力率を\( \ \cos \theta \ \)とすると,
\[
\begin{eqnarray}
P&=& 3S\cos \theta \\[ 5pt ]
&=& 3\cdot \frac {VI}{\sqrt {3}}\cdot \cos \theta \\[ 5pt ]
&=&\sqrt {3}VI \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。
②\( \ \mathrm {V -V } \ \)結線
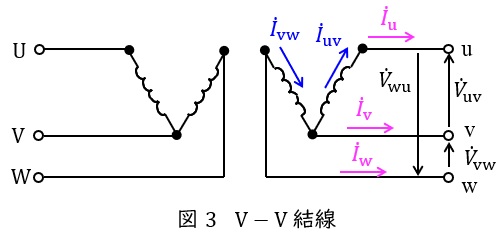
\( \ \mathrm {V -V } \ \)結線の変圧器の回路図とベクトル図を図3及び図4に示します。
図3において,負荷電流\( \ {\dot I}_{\mathrm {u}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {v}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {w}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}}&=& {\dot I}_{\mathrm {uv}} \\[ 5pt ]
{\dot I}_{\mathrm {v}}&=& {\dot I}_{\mathrm {vw}}-{\dot I}_{\mathrm {uv}} \\[ 5pt ]
{\dot I}_{\mathrm {w}}&=& -{\dot I}_{\mathrm {vw}} \\[ 5pt ]
\end{eqnarray}
\]
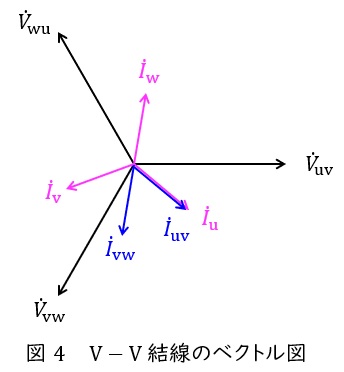
で求められ,ベクトル図上では図4のような関係となり,三相平衡である場合にはそれぞれの大きさの比は,
\[
\begin{eqnarray}
I_{\mathrm {u}}&=&I_{\mathrm {v}}&=&I_{\mathrm {w}}&=&I_{\mathrm {uv}}&=&I_{\mathrm {vw}} \\[ 5pt ]
\end{eqnarray}
\]
であることが分かります。したがって,各変圧器が分担する容量\( \ S \ \mathrm {[V\cdot A]} \ \)は,負荷の線間電圧を\( \ V_{\mathrm {uv}}=V_{\mathrm {vw}}=V_{\mathrm {wu}}=V \ \),負荷電流を\( \ I_{\mathrm {u}}=I_{\mathrm {v}}=I_{\mathrm {w}}=I \ \)とすると,
\[
\begin{eqnarray}
S&=& VI \\[ 5pt ]
\end{eqnarray}
\]
となります。変圧器全体の送電電力\( \ P_{\mathrm {V}} \ \mathrm {[W]} \ \)は力率を\( \ \cos \theta \ \)とすると,
\[
\begin{eqnarray}
P_{\mathrm {V}}&=& \sqrt {3}VI \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \mathrm {V -V } \ \)結線で得られる出力\( \ \mathrm {[V\cdot A]} \ \)は各変圧器の出力の\( \ \sqrt {3} \ \)倍となるため,利用率は,
\[
\begin{eqnarray}
利用率&=& \frac {\sqrt {3}VI}{2VI} \\[ 5pt ]
&=& \frac {\sqrt {3}}{2} → 86.6 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,\( \ \mathrm {V -V } \ \)結線と\( \ \mathrm {\Delta -\Delta } \ \)結線で同じ電力を出力する場合に必要となる変圧器の容量比は,
\[
\begin{eqnarray}
容量比&=& \frac {\displaystyle \frac {VI}{\sqrt {3}}}{VI} \\[ 5pt ]
&=& \frac {1}{\sqrt {3}} → 57.7 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ \mathrm {V -V } \ \)結線の出力は\( \ \mathrm {\Delta -\Delta } \ \)結線の\( \ 57.7 \ \mathrm {[%]} \ \)程度であることがわかります。
【解答】
(1)\( \ \mathrm {V} \ \)結線した場合の利用率は\( \ \displaystyle \frac {\sqrt {3}}{2} \ \left( = 0.866 \right) \ \)であることを説明
\( \ \mathrm {V} \ \)結線における相電圧を\( \ V \ \mathrm {[V]} \ \),相電流を\( \ I \ \mathrm {[A]} \ \)とすると,図3の通り,三相負荷に供給される線間電圧が\( \ V \ \mathrm {[V]} \ \),線電流は\( \ I \ \mathrm {[A]} \ \)となる。
このとき,三相負荷に供給される皮相電力\( \ S_{\mathrm {L}} \ \mathrm {[V\cdot A]} \ \)は,
\[
\begin{eqnarray}
S_{\mathrm {L}}&=& \sqrt {3}VI \\[ 5pt ]
\end{eqnarray}
\]
であり,必要な変圧器の容量\( \ S_{\mathrm {V}} \ \mathrm {[V\cdot A]} \ \)は,
\[
\begin{eqnarray}
S_{\mathrm {V}}&=& 2VI \\[ 5pt ]
\end{eqnarray}
\]
であるから,利用率は,
\[
\begin{eqnarray}
\frac {S_{\mathrm {L}}}{S_{\mathrm {V}}}&=& \frac {\sqrt {3}VI}{2VI} \\[ 5pt ]
&=& \frac {\sqrt {3}}{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)定格容量\( \ 100 \ \mathrm {[kV\cdot A]} \ \)の単相変圧器を\( \ \mathrm {V} \ \)結線にて配電した場合の最大容量\( \ \mathrm {[kV\cdot A]} \ \)
(1)より,三相負荷に供給される皮相電力\( \ S_{\mathrm {L}} \ \mathrm {[V\cdot A]} \ \)は,
\[
\begin{eqnarray}
S_{\mathrm {L}}&=& \sqrt {3}VI \\[ 5pt ]
\end{eqnarray}
\]
であり,単相変圧器一台あたりの容量\( \ VI=100 \ \mathrm {[kV\cdot A]} \ \)であるから,
\[
\begin{eqnarray}
S_{\mathrm {L}}&=& \sqrt {3}\times 100 \\[ 5pt ]
&≒& 173 \ \mathrm {[kV\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)単相変圧器を組み合わせた三相変圧器バンクと比較して一つの鉄心に三相分の巻線を施した三相変圧器の長所と短所
(ポイント)
・(1),(2)より,単相変圧器の場合は\( \ \mathrm {V} \ \)結線とできることが最大の特徴なので,それが三相変圧器の短所側の一つの解答となるかと思います。
・三相変圧器は重量を抑えることができ,それに伴い設置面積も小さくなり,コストが安くなる等のメリットがあります。
(試験センター解答例)
下記のような解答が,いずれか\( \ 1 \ \)項目ずつ記載されていればよい。
●長所
・鉄心材料の使用量が少なく,鉄損も少なくなるので効率が良い。
・使用材料が少なくて済むので質量が減少し,設置スペースや材料費も節約される。(質量が減少,設置スペースが節約及び経済的だけでも正解とする。)
・高電圧結線が外箱内でできるので,ブッシングが少なくできる。
●短所
・一相だけ故障しても三相平衡回路が成立しないので,変圧器全体が使用できなくなる。
・予備変圧器として三相変圧器バンクの場合には単相変圧器\( \ 1 \ \)台を予備とすればよいが,三相変圧器の場合には三相変圧器\( \ 1 \ \)台を予備としなくてはならないので,設置バンク数が少ないときには予備変圧器が割高となる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん