【問題】
【難易度】★★★☆☆(普通)
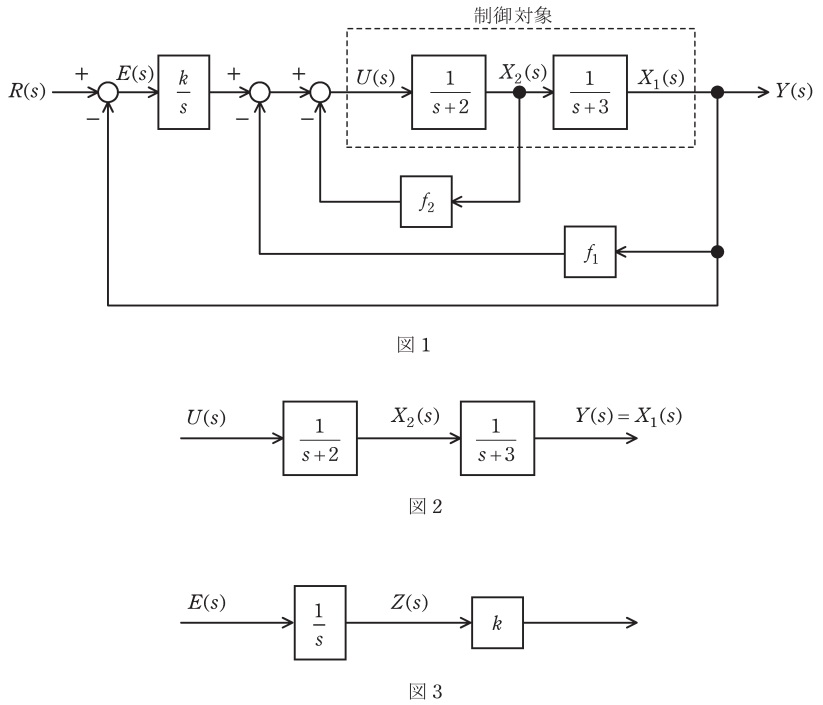
図1のフィードバック制御系について,次の問に答えよ。ただし,以下の設問において用いる\( \ x_{1}(t) \ \),\( \ x_{2}(t) \ \),\( \ u(t) \ \),\( \ y(t) \ \),\( \ r(t) \ \),\( \ e(t) \ \)及び\( \ z(t) \ \)のラプラス変換はそれぞれ,\( \ X_{1}(s) \ \),\( \ X_{2}(s) \ \),\( \ U(s) \ \),\( \ Y(s) \ \),\( \ R(s) \ \),\( \ E(s) \ \)及び\( \ Z(s) \ \)で表す。
(1) 図1の制御対象部分を示す図2において,状態変数を\( \ x_{1}(t) \ \),\( \ x_{2}(t) \ \),制御対象の入力と出力をそれぞれ\( \ u(t) \ \),\( \ y(t) \ \)とする。このとき,状態ベクトル\( \ \boldsymbol x (t)=\begin{bmatrix} x_{1}(t) & x_{2}(t) \end{bmatrix} ^{T} \ \)が満たす次の状態空間表現
\[
\begin{eqnarray}
\dot {\boldsymbol x} (t)&=& \boldsymbol {\mathrm {A}} \boldsymbol x (t) +\boldsymbol {\mathrm {b}} u (t), y(t)&=& \boldsymbol {\mathrm {c}} \boldsymbol x (t) \\[ 5pt ]
\end{eqnarray}
\]
における,\( \ \boldsymbol {\mathrm {A}} \ \),\( \ \boldsymbol {\mathrm {b}} \ \),\( \ \boldsymbol {\mathrm {c}} \ \)を求めよ。
(2) 図1の積分器を図3のように書き直して,変数\( \ Z(s) \ \)を新たに設けるとき,この時間関数\( \ z(t) \ \)は,関係式
\[
\begin{eqnarray}
\dot z (t)&=& r (t)-y(t)&=&r(t)-\boldsymbol {\mathrm {c}} \boldsymbol x (t) \\[ 5pt ]
\end{eqnarray}
\]
を満たす。また,入力\( \ u(t) \ \)は次のように書くことができる。
\[
\begin{eqnarray}
u (t)&=&-\boldsymbol {\mathrm {f}} \boldsymbol x (t)+kz(t),\boldsymbol {\mathrm {f}}=\begin{bmatrix} f_{1} & f_{2} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
積分器の出力である\( \ z(t) \ \)を状態変数として取り込み,状態ベクトルを\( \ \overline {\boldsymbol x} (t)=\begin{bmatrix} x_{1}(t) & x_{2}(t) & z(t) \end{bmatrix} ^{T} \ \)に拡大すると,図1のフィードバック制御系は次の状態空間表現
\[
\begin{eqnarray}
\dot {\overline {\boldsymbol x}} (t)&=& \overline {\boldsymbol {\mathrm {A}}} \overline {\boldsymbol x} (t) +\overline {\boldsymbol {\mathrm {b}}} r (t), y(t)&=& \overline {\boldsymbol {\mathrm {c}}} \ \overline {\boldsymbol x} (t) \\[ 5pt ]
\end{eqnarray}
\]
で記述できる。\( \ \overline {\boldsymbol {\mathrm {A}}} \ \),\( \ \overline {\boldsymbol {\mathrm {b}}} \ \),\( \ \overline {\boldsymbol {\mathrm {c}}} \ \)を\( \ \boldsymbol {\mathrm {A}} \ \),\( \ \boldsymbol {\mathrm {b}} \ \),\( \ \boldsymbol {\mathrm {c}} \ \),\( \ k \ \),\( \ \boldsymbol {\mathrm {f}} \ \),\( \ 0 \ \)及び\( \ 1 \ \)を用いて表せ。
(3) \( \ k=1 \ \),\( \ f_{1}=1 \ \),\( \ f_{2}=1 \ \)として,上記小問(2)の行列\( \ \overline {\boldsymbol {\mathrm {A}}} \ \)の固有値を与える特性多項式を示せ。
(4) \( \ k=1 \ \),\( \ f_{1}=1 \ \),\( \ f_{2}=1 \ \)として,図1のブロック線図の目標値\( \ R(s) \ \)から出力\( \ Y(s) \ \)までの伝達関数を求めよ。
【ワンポイント解説】
現代制御理論からの出題です。近年は自動制御も選択者が多いのか少し捻った問題が出題されるようです。(2)や(3)がやや応用問題と言えますが,冷静に解けばそれほど難易度が高い問題ではないので落ち着いて解くようにしましょう。
1.特性多項式
\( \ \boldsymbol {\mathrm {A}} \ \)の特性多項式は単位行列\( \ \boldsymbol I \ \)とすると,
\[
\begin{eqnarray}
\left| s\boldsymbol I-\boldsymbol {\mathrm {A}}\right| &=&0 \\[ 5pt ]
\end{eqnarray}
\]
で与えられる多項式を言い,これにより求められる\( \ s \ \)の値を固有値と言います。
【解答】
(1)\( \ \boldsymbol {\mathrm {A}} \ \),\( \ \boldsymbol {\mathrm {b}} \ \),\( \ \boldsymbol c \ \)を求める
図2より,
\[
\begin{eqnarray}
X_{2}(s) &=&\frac {1}{s+2}U(s) &→& sX_{2}(s)&=&-2X_{2}(s)+U(s) \\[ 5pt ]
X_{1}(s) &=&\frac {1}{s+3}X_{2}(s) &→& sX_{1}(s)&=&-3X_{1}(s)+X_{2}(s) \\[ 5pt ]
Y(s) &=&X_{1}(s) \\[ 5pt ]
\end{eqnarray}
\]
が成り立つので,両辺をラプラス逆変換すると,
\[
\begin{eqnarray}
\dot x_{2}(t)&=&-2x_{2}(t)+u(t) \\[ 5pt ]
\dot x_{1}(t)&=&-3x_{1}(t)+x_{2}(t) \\[ 5pt ]
y(t) &=&x_{1}(t) \\[ 5pt ]
\end{eqnarray}
\]
となる。上式を状態空間表現すると,
\[
\begin{eqnarray}
\begin{bmatrix} \dot x_{1}(t) \\ \dot x_{2}(t) \end{bmatrix}&=&\begin{bmatrix} -3 & 1 \\ 0 & -2 \end{bmatrix}\begin{bmatrix} x_{1}(t) \\ x_{2}(t) \end{bmatrix}+\begin{bmatrix} 0 \\ 1 \end{bmatrix}u(t) \\[ 5pt ]
y(t) &=&\begin{bmatrix} 1 & 0 \end{bmatrix}\begin{bmatrix} x_{1}(t) \\ x_{2}(t) \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\displaystyle \boldsymbol {\mathrm {A}}=\begin{bmatrix} -3 & 1 \\ 0 & -2 \end{bmatrix},\displaystyle \boldsymbol {\mathrm {b}}=\begin{bmatrix} 0 \\ 1 \end{bmatrix},\displaystyle \boldsymbol {\mathrm {c}}=\begin{bmatrix} 1 & 0 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ \overline {\boldsymbol {\mathrm {A}}} \ \),\( \ \overline {\boldsymbol {\mathrm {b}}} \ \),\( \ \overline {\boldsymbol c} \ \)を\( \ \boldsymbol {\mathrm {A}} \ \),\( \ \boldsymbol {\mathrm {b}} \ \),\( \ \boldsymbol {\mathrm {c}} \ \),\( \ k \ \),\( \ \boldsymbol {\mathrm {f}} \ \),\( \ 0 \ \)及び\( \ 1 \ \)を用いて表す
(1)及び題意より,
\[
\begin{eqnarray}
\dot {\boldsymbol x} (t)&=& \boldsymbol {\mathrm {A}} \boldsymbol x (t) +\boldsymbol {\mathrm {b}} u (t)& ・・・・・・・・・・・・・・・・・ ①& \\[ 5pt ]
u (t)&=&-\boldsymbol {\mathrm {f}} \boldsymbol x (t)+kz(t)& ・・・・・・・・・・・・・・・・・ ② & \\[ 5pt ]
\end{eqnarray}
\]
であるから,②を①に代入すると,
\[
\begin{eqnarray}
\dot {\boldsymbol x} (t)&=& \boldsymbol {\mathrm {A}} \boldsymbol x (t) +\boldsymbol {\mathrm {b}} \left[ -\boldsymbol {\mathrm {f}} \boldsymbol x (t)+kz(t)\right] \\[ 5pt ]
\dot {\boldsymbol x} (t)&=& \left( \boldsymbol {\mathrm {A}} -\boldsymbol {\mathrm {b}} \boldsymbol {\mathrm {f}}\right) \boldsymbol x (t) +\boldsymbol {\mathrm {b}} kz(t)& ・・・・・・・・・・ ③ & \\[ 5pt ]
\end{eqnarray}
\]
となる。また,題意より,
\[
\begin{eqnarray}
\dot z (t)&=&-\boldsymbol {\mathrm {c}} \boldsymbol x (t)+r(t) & ・・・・・・・・・・・・・・・・・・ ④ & \\[ 5pt ]
\end{eqnarray}
\]
であるから,③,④を状態空間表現をすると,
\[
\begin{eqnarray}
\begin{bmatrix} \dot {\boldsymbol x} (t) \\ \dot z (t) \end{bmatrix}&=&\begin{bmatrix} \boldsymbol {\mathrm {A}} -\boldsymbol {\mathrm {b}} \boldsymbol {\mathrm {f}} & \boldsymbol {\mathrm {b}} k \\ -\boldsymbol {\mathrm {c}} & 0 \end{bmatrix}\begin{bmatrix} \boldsymbol x (t) \\ z(t) \end{bmatrix}+\begin{bmatrix} \boldsymbol 0 \\ 1 \end{bmatrix}r(t) & ・・・・・ ⑤ & \\[ 5pt ]
\end{eqnarray}
\]
となる。また,\( \ y(t)= \boldsymbol {\mathrm {c}} \boldsymbol x (t) \ \)であるから,状態空間表現をすると,
\[
\begin{eqnarray}
y(t)&=&\begin{bmatrix} \boldsymbol {\mathrm {c}} & 0 \end{bmatrix}\begin{bmatrix} \boldsymbol x (t) \\ z(t) \end{bmatrix}& ・・・・・・・・・・・・・・・・・・ ⑥ & \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,⑤,⑥より,
\[
\begin{eqnarray}
\displaystyle \overline {\boldsymbol {\mathrm {A}}}=\begin{bmatrix} \boldsymbol {\mathrm {A}} -\boldsymbol {\mathrm {b}} \boldsymbol {\mathrm {f}} & \boldsymbol {\mathrm {b}} k \\ -\boldsymbol c & 0 \end{bmatrix},\overline {\displaystyle \boldsymbol {\mathrm {b}}}=\begin{bmatrix} \boldsymbol 0 \\ 1 \end{bmatrix},\displaystyle \overline {\boldsymbol c}=\begin{bmatrix} \boldsymbol c & 0 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \overline {\boldsymbol {\mathrm {A}}} \ \)の固有値を与える特性多項式
\[
\begin{eqnarray}
\boldsymbol {\mathrm {A}} -\boldsymbol {\mathrm {b}} \boldsymbol {\mathrm {f}}&=&\begin{bmatrix} -3 & 1 \\ 0 & -2 \end{bmatrix}-\begin{bmatrix} 0 \\ 1 \end{bmatrix}\begin{bmatrix} 1 & 1 \end{bmatrix} \\[ 5pt ]
&=&\begin{bmatrix} -3 & 1 \\ 0 & -2 \end{bmatrix}-\begin{bmatrix} 0 & 0 \\ 1 & 1 \end{bmatrix} \\[ 5pt ]
&=&\begin{bmatrix} -3 & 1 \\ -1 & -3 \end{bmatrix} \\[ 5pt ]
\boldsymbol {\mathrm {b}} k&=&\begin{bmatrix} 0 \\ 1 \end{bmatrix}1 \\[ 5pt ]
&=&\begin{bmatrix} 0 \\ 1 \end{bmatrix} \\[ 5pt ]
-\boldsymbol {\mathrm {c}}&=&-\begin{bmatrix} 1 & 0 \end{bmatrix} \\[ 5pt ]
&=&\begin{bmatrix} -1 & 0 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
\displaystyle \overline {\boldsymbol {\mathrm {A}}}&=&\begin{bmatrix} -3 & 1 & 0 \\ -1 & -3 & 1 \\ -1 & 0 & 0 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「1.特性多項式」より,\( \ \overline {\boldsymbol {\mathrm {A}}} \ \)の固有値を与える特性多項式は,
\[
\begin{eqnarray}
\left| s\boldsymbol I-\overline {\boldsymbol {\mathrm {A}}}\right| &=&\left| \begin{bmatrix} s & 0 & 0 \\ 0 & s & 0 \\ 0 & 0 & s \end{bmatrix} -\begin{bmatrix} -3 & 1 & 0 \\ -1 & -3 & 1 \\ -1 & 0 & 0 \end{bmatrix} \right| \\[ 5pt ]
&=&\begin{vmatrix} s+3 & -1 & 0 \\ 1 & s+3 & -1 \\ 1 & 0 & s \end{vmatrix} \\[ 5pt ]
&=&\left( s+3\right) \left( s+3\right) s+(-1)\cdot (-1) \cdot 1-(-1)\cdot 1\cdot s \\[ 5pt ]
&=&s^{3}+6s^{2}+10s+1 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)目標値\( \ R(s) \ \)から出力\( \ Y(s) \ \)までの伝達関数
\( \ k=1 \ \),\( \ f_{1}=1 \ \),\( \ f_{2}=1 \ \)に注意して,フィードバック制御系に関して成り立つ等式を考えると,
\[
\begin{eqnarray}
\left[ [ R(s)-Y(s) ] \frac {1}{s}-Y(s)-X_{2}(s)\right] \frac {1}{s+2} &=&X_{2}(s) & ・・・・・・ ⑦ & \\[ 5pt ]
X_{2}(s)\cdot \frac {1}{s+3} &=&Y(s) & ・・・・・・ ⑧ & \\[ 5pt ]
\end{eqnarray}
\]
となるので,⑧を⑦に代入して整理すると,
\[
\begin{eqnarray}
\left[ [ R(s)-Y(s) ] \frac {1}{s}-Y(s)-\left( s+3\right) Y(s)\right] \frac {1}{s+2} &=&\left( s+3\right) Y(s) \\[ 5pt ]
\left[ R(s)-Y(s) \right] \frac {1}{s}-Y(s)-\left( s+3\right) Y(s) &=&\left( s+2\right) \left( s+3\right) Y(s) \\[ 5pt ]
R(s)-Y(s)-sY(s)-s\left( s+3\right) Y(s) &=&s\left( s+2\right) \left( s+3\right) Y(s) \\[ 5pt ]
R(s)&=&\left[ s\left( s+2\right) \left( s+3\right) +s\left( s+3\right) +s +1 \right] Y(s) \\[ 5pt ]
\frac {Y(s)}{R(s)}&=&\frac {1}{s^{3}+6s^{2}+10s+1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん