【問題】
【難易度】★☆☆☆☆(易しい)
単相変圧器について次の問に答えよ。
(1) 下記に示す記号を用いて,単相変圧器の簡易等価回路(\( \ \mathrm {L} \ \)型等価回路)を描け。
【等価回路に使用する記号】
\( \ V_{\mathrm {1}} \ \):一次端子電圧,\( \ I_{\mathrm {1}} \ \):入力電流,\( \ I_{\mathrm {0}} \ \):励磁電流,\( \ r_{\mathrm {s}} \ \):一次側換算全巻線抵抗,\( \ x_{\mathrm {s}} \ \):一次側換算全漏れリアクタンス,\( \ g_{\mathrm {0}} \ \):一次側励磁コンダクタンス,\( \ b_{\mathrm {0}} \ \):一次側励磁サセプタンス
(2) ある単相変圧器を定格周波数の電源を用いて試験したところ,次のような結果となった。
二次端子を開放して無負荷試験を行い,定格電圧\( \ V_{\mathrm {NL}} \ \mathrm {[V]} \ \)を一次端子に加えたところ,入力電流\( \ I_{\mathrm {1}}=I_{\mathrm {NL}} \ \mathrm {[A]} \ \),入力電力は\( \ P_{\mathrm {NL}} \ \mathrm {[W]} \ \)であった。さらに,二次端子を短絡して短絡試験を行い,二次電流が定格電流になるような電圧\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \)を一次端子に加えたところ,入力電流\( \ I_{\mathrm {1}}=I_{\mathrm {s}} \ \mathrm {[A]} \ \),入力電力は\( \ P_{\mathrm {s}} \ \mathrm {[W]} \ \)であった。
試験により得られた測定値から,等価回路定数\( \ r_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \),\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \),\( \ g_{\mathrm {o}} \ \mathrm {[S]} \ \),\( \ b_{\mathrm {o}} \ \mathrm {[S]} \ \)を求める式を導出せよ。導出にあたっては,次のような仮定を用いること。また,導出の経過について,考え方を説明すること。
(Ⅰ)無負荷試験においては,入力した電力はすべて鉄損である。
(Ⅱ)短絡試験においては,励磁電流は無視する。
【ワンポイント解説】
変圧器の無負荷試験と短絡試験に関する問題です。
無負荷試験と短絡試験は\( \ 2 \ \)種の頃から過去問でも出題されている内容なので,多くの受験生が選択したと考えられます。
ぜひ完答を目指して頂きたい問題です。
1.変圧器の\( \ \mathrm {L} \ \)形等価回路(一次換算)
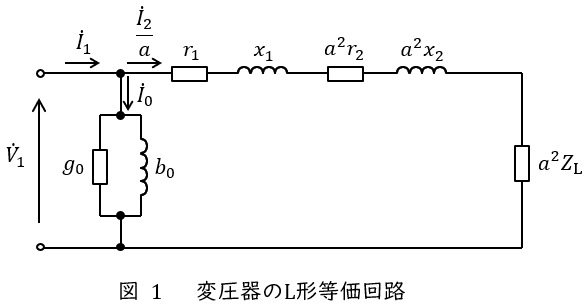
変圧器の一次換算\( \ \mathrm {L} \ \)形等価回路を図1に示します。ただし,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)は二次電流,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2} \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2} \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンス,\( \ Z_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)は負荷,\( \ g_{\mathrm {o}} \ \mathrm {[S]} \ \)は励磁コンダクタンス,\( \ b_{\mathrm {o}} \ \mathrm {[S]} \ \)は励磁サセプタンス,\( \ a \ \)は変圧比(巻数比)となります。
2.無負荷試験の等価回路
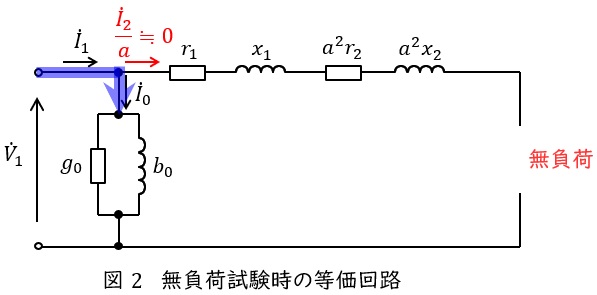
変圧器の無負荷試験は二次側(もしくは一次側)を開放して,一次側(もしくは二次側)に定格電圧を加える試験です。電源から出た電流はほぼ励磁回路に流れるので,一次側(もしくは二次側)に定格電圧\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)をかけ,そのときの電力\( \ P_{\mathrm {0}} \ \mathrm {[W]} \ \)と電流\( \ I_{\mathrm {0}} \ \mathrm {[A]} \ \)を測定すれば,励磁コンダクタンス\( \ g_{0} \ \mathrm {[S]} \ \)と励磁サセプタンス\( \ b_{0} \ \mathrm {[S]} \ \)をそれぞれ,
\[
\begin{eqnarray}
P_{\mathrm {0}} &=&g_{0}V_{\mathrm {n}} ^{2} \\[ 5pt ]
g_{0}&=&\frac {P_{\mathrm {0}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ]
b_{0}&=&\sqrt {Y_{\mathrm {0}}^{2}-g_{\mathrm {0}}^{2}} \\[ 5pt ]
&=&\sqrt {\left( \frac {I_{\mathrm {0}}}{V_{\mathrm {n}}}\right) ^{2}-g_{\mathrm {0}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求めることができます。
3.短絡試験の等価回路
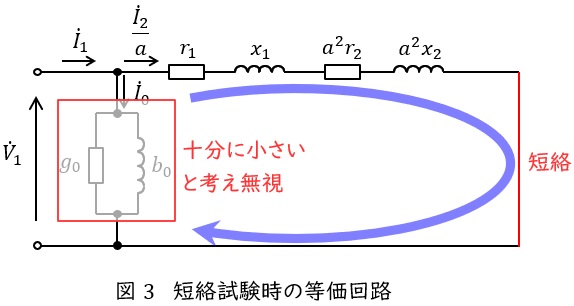
変圧器の短絡試験は二次側を短絡して,定格電流を流すように一次側にインピーダンス電圧を加える試験です。一次側に定格電流\( \ I_{\mathrm {1n}} \ \mathrm {[A]} \ \)が流れるように電圧\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \)をかけ,そのときの電力\( \ P_{\mathrm {s}} \ \mathrm {[W]} \ \)を測定すれば,一次巻線抵抗と二次巻線抵抗の一次換算値の合計\( \ r=r_{1}+a^{2}r_{2} \ \)と,一次漏れリアクタンスと二次漏れリアクタンスの一次換算値の合計\( \ x=x_{1}+a^{2}x_{2} \ \)をそれぞれ,
\[
\begin{eqnarray}
P_{\mathrm {s}} &=&rI_{\mathrm {1n}}^{2} \\[ 5pt ]
r&=&\frac {P_{\mathrm {s}}}{I_{\mathrm {1n}}^{2}} \\[ 5pt ]
x&=&\sqrt {Z_{\mathrm {s}}^{2}-r^{2}} \\[ 5pt ]
&=&\sqrt {\left( \frac {V_{\mathrm {s}}}{I_{\mathrm {1n}}}\right) ^{2}-r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求めることができます。
【解答】
(1)単相変圧器の簡易等価回路(\( \ \mathrm {L} \ \)型等価回路)
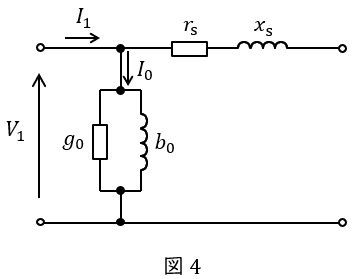
ワンポイント解説「1.変圧器の\( \ \mathrm {L} \ \)形等価回路(一次換算)」の通り,\( \ \mathrm {L} \ \)型等価回路は,抵抗及びリアクタンスが一次側換算全抵抗及び全漏れリアクタンスであることに注意すると図4のようになる。
(2)\( \ r_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \),\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \),\( \ g_{\mathrm {o}} \ \mathrm {[S]} \ \),\( \ b_{\mathrm {o}} \ \mathrm {[S]} \ \)を求める式
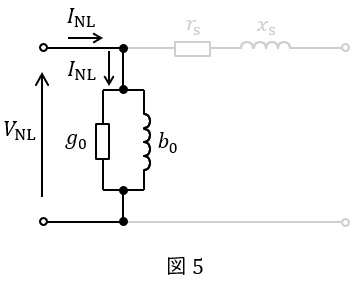
「(Ⅰ)無負荷試験においては,入力した電力はすべて鉄損である。」という仮定から,無負荷試験時の等価回路は図5のようになる。図5において\( \ g_{\mathrm {o}} \ \mathrm {[S]} \ \)で消費される電力が\( \ P_{\mathrm {NL}} \ \mathrm {[W]} \ \)であるから,
\[
\begin{eqnarray}
P_{\mathrm {NL}} &=&g_{\mathrm {o}}{V_{\mathrm {NL}}}^{2} \\[ 5pt ]
g_{\mathrm {o}}&=&\frac {P_{\mathrm {NL}}}{{V_{\mathrm {NL}}}^{2}} \ \mathrm {[S]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,オームの法則より,
\[
\begin{eqnarray}
\sqrt {{g_{\mathrm {o}}}^{2}+{b_{\mathrm {o}}}^{2}} &=&\frac {I_{\mathrm {NL}}}{V_{\mathrm {NL}}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,これを\( \ b_{\mathrm {o}} \ \mathrm {[S]} \ \)について整理すれば,
\[
\begin{eqnarray}
{g_{\mathrm {o}}}^{2}+{b_{\mathrm {o}}}^{2} &=&\left( \frac {I_{\mathrm {NL}}}{V_{\mathrm {NL}}}\right) ^{2} \\[ 5pt ]
{b_{\mathrm {o}}}^{2} &=&\left( \frac {I_{\mathrm {NL}}}{V_{\mathrm {NL}}}\right) ^{2}-{g_{\mathrm {o}}}^{2} \\[ 5pt ]
b_{\mathrm {o}}&=&\sqrt {\left( \frac {I_{\mathrm {NL}}}{V_{\mathrm {NL}}}\right) ^{2}-{g_{\mathrm {o}}}^{2}} \\[ 5pt ]
&=&\sqrt {\left( \frac {I_{\mathrm {NL}}}{V_{\mathrm {NL}}}\right) ^{2}-\left( \frac {P_{\mathrm {NL}}}{{V_{\mathrm {NL}}}^{2}}\right) ^{2}} \ \mathrm {[S]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
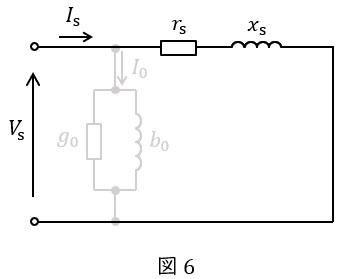
また,「(Ⅱ)短絡試験においては,励磁電流は無視する。」という仮定から,短絡試験時の等価回路は図6のようになる。図6において\( \ r_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)で消費される電力が\( \ P_{\mathrm {s}} \ \mathrm {[W]} \ \)であるから,
\[
\begin{eqnarray}
P_{\mathrm {s}} &=&r_{\mathrm {s}}{I_{\mathrm {s}}}^{2} \\[ 5pt ]
r_{\mathrm {s}}&=&\frac {P_{\mathrm {s}}}{{I_{\mathrm {s}}}^{2}} \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,オームの法則より,
\[
\begin{eqnarray}
\sqrt {{r_{\mathrm {s}}}^{2}+{x_{\mathrm {s}}}^{2}} &=&\frac {V_{\mathrm {s}}}{I_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,これを\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)について整理すれば,
\[
\begin{eqnarray}
{r_{\mathrm {s}}}^{2}+{x_{\mathrm {s}}}^{2} &=&\left( \frac {V_{\mathrm {s}}}{I_{\mathrm {s}}}\right) ^{2} \\[ 5pt ]
{x_{\mathrm {s}}}^{2} &=&\left( \frac {V_{\mathrm {s}}}{I_{\mathrm {s}}}\right) ^{2}-{r_{\mathrm {s}}}^{2} \\[ 5pt ]
x_{\mathrm {s}}&=&\sqrt {\left( \frac {V_{\mathrm {s}}}{I_{\mathrm {s}}}\right) ^{2}-{r_{\mathrm {s}}}^{2}} \\[ 5pt ]
&=&\sqrt {\left( \frac {V_{\mathrm {s}}}{I_{\mathrm {s}}}\right) ^{2}-\left( \frac {P_{\mathrm {s}}}{{I_{\mathrm {s}}}^{2}}\right) ^{2}} \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん