【問題】
【難易度】★★★☆☆(普通)
図1及び図3に示す制御系において,次の問に答えよ。ただし,\( \ R (s) \ \)は目標値,\( \ E (s) \ \)は偏差,\( \ U (s) \ \)は操作量,\( \ Y (s) \ \)は出力であり,\( \ G (s) \ \)は制御対象の伝達関数,\( \ K \ \)は定数ゲインとする。
(1) 図1において\( \ \displaystyle G(s) =\frac {1}{s} \ \)のとき,\( \ K>0 \ \)ならば図1のフィードバック制御系が安定となることを示せ。
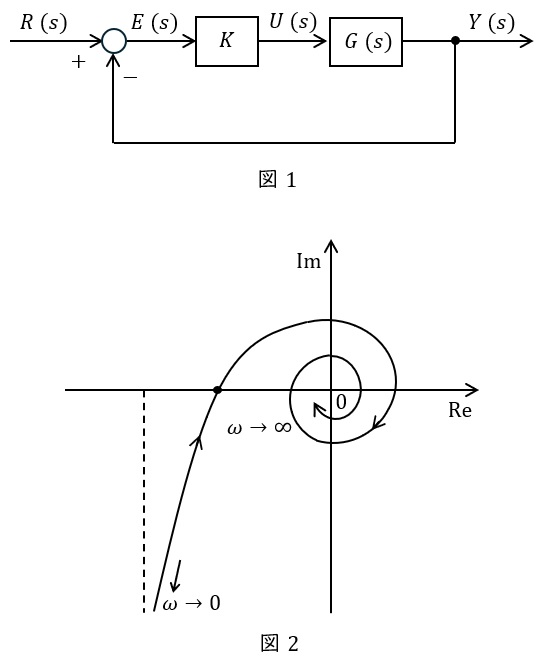
(2) 図1において\( \ \displaystyle G(s) =\frac {1}{s}\mathrm {e}^{-Ls} \ \)のとき,むだ時間\( \ L \ \)を含む図1の制御系の安定性を解析するために,\( \ \displaystyle KG (\mathrm {j}\omega ) =K\frac {\mathrm {e}^{-\mathrm {j}\omega L}}{\mathrm {j}\omega } \ \)のベクトル軌跡の概形を描くと図2のようになる。図1の制御系を安定にする\( \ K \ \)の範囲を求めよ。
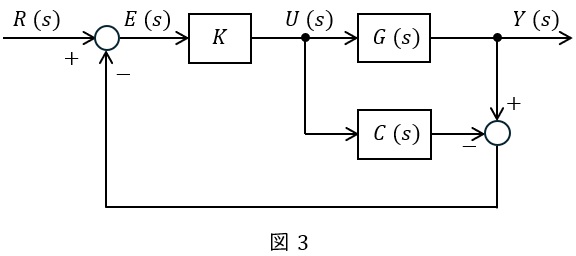
(3) \( \ \displaystyle G(s) =\frac {1}{s}\mathrm {e}^{-Ls} \ \)のむだ時間を補償するために,補償器\( \ C (s) \ \)を付加した図3のフィードバック制御系を考える。\( \ \displaystyle C(s) =\frac {1}{s}\left( \mathrm {e}^{-Ls}-1\right) \ \)とするとき,\( \ R (s) \ \)から\( \ Y (s) \ \)までの伝達関数を求めよ。
(4) 上記(3)の結果から,図3の制御系を安定にする\( \ K \ \)の範囲を求めよ。
【ワンポイント解説】
ナイキストの安定判別法を用いた制御系の安定判別をする問題です。
(2)の難易度が高めですが,(3)及び(4)は連動していないため(1),(3),(4)が解ければ十分に合格圏内となると考えて良いかと思います。
1.開ループ伝達関数と閉ループ伝達関数
ブロック線図において,フィードバック制御のループを考慮しない関数を開ループ伝達関数,ループを考慮する関数を閉ループ伝達関数,ループを一巡だけ考慮する関数を一巡伝達関数といいます。
図3の例においては,開ループ伝達関数\( \ W_{\mathrm {o}} \left( s \right) \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {o}} \left( s \right) &=& G \left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
閉ループ伝達関数\( \ W \left( s \right) \ \)は,
\[
\begin{eqnarray}
W \left( s \right) &=&\frac {G \left( s \right) }{1+G \left( s \right) H \left( s \right) } \\[ 5pt ]
\end{eqnarray}
\]
一巡伝達関数\( \ W_{\mathrm {r}} \left( s \right) \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {r}} \left( s \right) &=& G \left( s \right) H \left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.特性根による安定判別
閉ループ伝達関数の特性方程式,例えば図3の例においては\( \ 1+G \left( s \right) H \left( s \right) =0 \ \)において,\( \ s \ \)について解いた根の実数部がすべて負である場合には安定,一つでも根の実数部が正である場合には不安定となります。
解の公式がある二次方程式までは特性根による安定判別が有効となります。
3.ナイキストの安定判別法
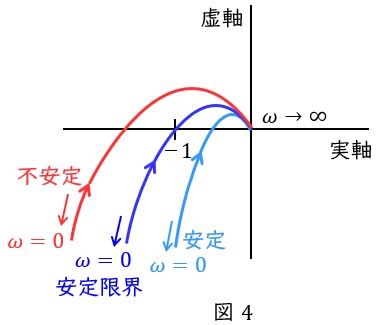
図4に示すような周波数伝達関数のベクトル軌跡をナイキスト線図といい,ナイキスト線図による安定判別をナイキストの安定判別法といいます。
一巡伝達関数\( \ W_{\mathrm {r}} \left( \mathrm {j}\omega \right) \ \)において,角周波数\( \ \omega \ \)を\( \ 0 \ \)から\( \ \infty \ \)まで変化させたときのベクトル軌跡を描いたとき,
実軸との交点が\( \left( -1 , \mathrm {j}0\right) \)より右側であれば安定
実軸との交点が\( \left( -1 , \mathrm {j}0\right) \)であれば安定限界
実軸との交点が\( \left( -1 , \mathrm {j}0\right) \)より左側であれば不安定
となります。
【解答】
(1)\( \ \displaystyle G(s) =\frac {1}{s} \ \)のとき,\( \ K>0 \ \)ならば図1のフィードバック制御系が安定となることを示す
図1の閉ループ伝達関数\( \ W(s) \ \)は,ワンポイント解説「1.開ループ伝達関数と閉ループ伝達関数」の通り,
\[
\begin{eqnarray}
W \left( s \right) &=&\frac {KG \left( s \right) }{1+KG \left( s \right) } \\[ 5pt ]
&=&\frac {\displaystyle \frac {K}{s}}{1+\displaystyle \frac {K}{s}} \\[ 5pt ]
&=&\frac {K}{s+K} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,特定方程式は\( \ s+K=0 \ \)となるので,特性根は\( \ s=-K \ \)となり,ワンポイント解説「2.特性根による安定判別」の通り,\( \ K>0 \ \)ならば根が負となるので安定となる。
(2)\( \ \displaystyle G(s) =\frac {1}{s}\mathrm {e}^{-Ls} \ \)のとき,図1の制御系を安定にする\( \ K \ \)の範囲
図1の一巡ループ伝達関数\( \ W_{r}(s) \ \)は,
\[
\begin{eqnarray}
W_{r} \left( s \right) &=& KG \left( s \right) \\[ 5pt ]
&=& \frac {K}{s}\mathrm {e}^{-Ls} \\[ 5pt ]
\end{eqnarray}
\]
であり,この周波数伝達関数\( \ W_{r}(\mathrm {j}\omega ) \ \)は,
\[
\begin{eqnarray}
W_{r} \left( \mathrm {j}\omega \right) &=& \frac {K}{\mathrm {j}\omega }\mathrm {e}^{-\mathrm {j}\omega L} \\[ 5pt ]
&=& -\mathrm {j}\frac {K}{\omega }\left( \cos \omega L -\mathrm {j}\sin \omega L\right) \\[ 5pt ]
&=& -\frac {K}{\omega }\sin \omega L-\mathrm {j}\frac {K}{\omega }\cos \omega L \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「3.ナイキストの安定判別法」の通り,図2より,\( \ \omega \ \)を\( \ 0 \ \)から徐々に大きくしていき,実軸と初めて交わる点が\( \ \left( -1 , \mathrm {j}0\right) \ \)より右側であれば安定となるため,実軸との交点は上式の虚数部が零であることから,
\[
\begin{eqnarray}
\frac {K}{\omega }\cos \omega L &=&0 \\[ 5pt ]
\cos \omega L &=&0 \\[ 5pt ]
\omega L&=& \frac {\pi }{2},\frac {3\pi }{2},\frac {5\pi }{2},\cdots \\[ 5pt ]
\omega &=& \frac {\pi }{2L},\frac {3\pi }{2L},\frac {5\pi }{2L},\cdots \\[ 5pt ]
\end{eqnarray}
\]
となり,図2より初めて交わる点は\( \ \displaystyle \omega =\frac {\pi }{2L} \ \)の時であることがわかる。これを\( \ W_{r}(\mathrm {j}\omega ) \ \)の実数部に代入し,実数部が\( \ -1 \ \)より大きければ良いので,
\[
\begin{eqnarray}
-\frac {K}{\omega }\sin \omega L &>& -1 \\[ 5pt ]
-\frac {K}{\displaystyle \frac {\pi }{2L}}\sin \frac {\pi }{2L}\cdot L &>& -1 \\[ 5pt ]
-\frac {2KL}{\pi}\sin \frac {\pi }{2} &>& -1 \\[ 5pt ]
-\frac {2KL}{\pi} &>& -1 \\[ 5pt ]
\frac {2KL}{\pi} &<& 1 \\[ 5pt ]
K &<& \frac {\pi}{2L} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,(1)より,むだ時間を考慮しない場合において\( \ K≦0 \ \)が不安定であることがわかっているので,安定となる条件は\( \ \displaystyle 0<K<\frac {\pi}{2L} \ \)と求められる。
(3)図3における\( \ R (s) \ \)から\( \ Y (s) \ \)までの伝達関数
図3において,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
U(s)&=& KE(s) &・・・・・・・・・・・・ ①&\\[ 5pt ]
Y(s)&=& G(s)U(s) &・・・・・・・・・・・・ ②& \\[ 5pt ]
E(s)&=&R(s)-\left\{ Y(s)-C(s)U(s) \right\} &・・・・・・・・・・・・ ③& \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
となるので,①を②,③に代入して整理すれば,
\[
\begin{eqnarray}
Y(s)&=& KG(s)E(s) \\[ 5pt ]
E(s)&=& \frac {Y(s)}{KG(s)} &・・・・・・・・・ ②^{\prime }& \\[ 5pt ]
E(s)&=&R(s)-\left\{ Y(s)-KC(s)E(s) \right\} \\[ 5pt ]
E(s)&=&R(s)- Y(s)+KC(s)E(s) \\[ 5pt ]
\left\{ 1-KC(s)\right\} E(s)&=&R(s)- Y(s) &・・・・・・・・・ ③^{\prime }& \\[ 5pt ]
\end{eqnarray}
\]
となる。さらに\( \ ②^{\prime } \ \)を\( \ ③^{\prime } \ \)に代入して整理すれば,
\[
\begin{eqnarray}
\left\{ 1-KC(s)\right\} \frac {Y(s)}{KG(s)}&=&R(s)- Y(s) \\[ 5pt ]
\frac {1-KC(s)}{KG(s)}Y(s)+Y(s)&=&R(s) \\[ 5pt ]
\frac {1-KC(s)+KG(s)}{KG(s)}Y(s)&=&R(s) \\[ 5pt ]
\frac {Y(s)}{R(s)}&=&\frac {KG(s)}{1-KC(s)+KG(s)} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これに\( \ \displaystyle G(s) =\frac {1}{s}\mathrm {e}^{-Ls} \ \)及び\( \ \displaystyle C(s) =\frac {1}{s}\left( \mathrm {e}^{-Ls}-1\right) \ \)を代入すると,
\[
\begin{eqnarray}
\frac {Y(s)}{R(s)}&=&\frac {\displaystyle K\cdot \frac {1}{s}\mathrm {e}^{-Ls}}{\displaystyle 1-K\cdot \frac {1}{s}\left( \mathrm {e}^{-Ls}-1\right)+K\cdot \frac {1}{s}\mathrm {e}^{-Ls}} \\[ 5pt ]
&=&\frac {\displaystyle K\mathrm {e}^{-Ls}}{\displaystyle s-K\left( \mathrm {e}^{-Ls}-1\right)+K\mathrm {e}^{-Ls}} \\[ 5pt ]
&=&\frac {\displaystyle K\mathrm {e}^{-Ls}}{s+K} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)図3の制御系を安定にする\( \ K \ \)の範囲
(3)解答式において,\( \ \mathrm {e}^{-Ls} \ \)はむだ時間であるため,安定性は\( \ \displaystyle \frac {\displaystyle K}{s+K} \ \)を考えればよい。したがって,特性方程式\( \ s+K=0 \ \)より,特性根は\( \ s=-K \ \)となるため,ワンポイント解説「2.特性根による安定判別」の通り,根が負となる安定にする\( \ K \ \)の範囲は\( \ K>0 \ \)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん