《理論》〈電子理論〉[R06:問6]円電流が作る磁界中を通過する電子の運動に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，円電流が作る磁界中を通過する電子の運動に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。なお，電子の質量を$ \ m \ $，電荷量を$ \ -e \left( e＞0 \right) \ $とし，電子の質量の変化は無視する。

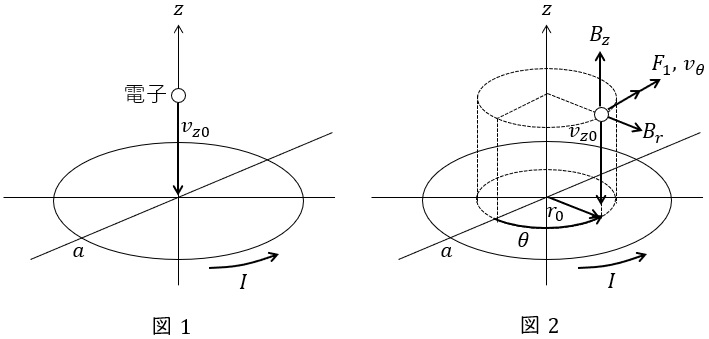
図1のように，原点を中心とする半径$ \ a \ $の円があり，その円周上に，図に示す方向に一定の電流$ \ I \left( ＞0 \right) \ $が流れている。円筒座標系の点$ \ \left( r，\theta ，z\right) \ $における，円電流$ \ I \ $が作る磁束密度ベクトル$ \ \boldsymbol B \ $を，$ \ \boldsymbol B=\left( B_{r}，B_{\theta }，B_{z}\right) \ $のように表す。

一つの電子が$ \ z \ $軸上を，$ \ z \ $軸の正の領域から速度$ \ v_{z0} \left( ＜0 \right) \ $で$ \ z \ $軸の負の方向に運動している状況を考える。円電流$ \ I \ $が作る磁束密度は，$ \ z \ $軸上では対称性から，$ \ z \ $軸方向の成分$ \ B_{z} \ $以外は$ \ 0 \ $であり，電子が磁界から受けるローレンツ力の大きさは$ \ \fbox {　（１）　} \ $である。

次に，図2のように，電子が$ \ z \ $軸と平行で距離$ \ r_{0} \left( 0＜r_{0}≪a \right) \ $だけ離れた軸上を運動する場合を考える。電子の速度の$ \ z \ $方向成分を$ \ v_{z0} \left( ＜0 \right) \ $，その他の方向の速度成分は$ \ 0 \ $とする。$ \ r_{0}≠0 \ $の場合には，$ \ B_{r} \ $は$ \ 0 \ $ではなく，電子の速さ$ \ \left| v_{z0}\right| \ $が極めて高速であれば，電子はごく短い時間$ \ \mathit {\Delta } t \ $でのみ磁界から力を受けると近似できる。$ \ B_{r} \ $によって電子が受けるローレンツ力$ \ F_{1} \ $は，図2に示すような半径$ \ r_{0} \ $の円の接線に沿って$ \ \theta \ $が増加する方向（$ \ \theta + \ $方向と定義する）を正にとると，符号も含めて$ \ F_{1}= \ \fbox {　（２）　} \ $と表される。その結果，$ \ \theta + \ $方向に速度$ \ v_{\theta } \left( ＞0 \right) \ $が生じる。ニュートンの第$ \ 2 \ $法則より，$ \ v_{\theta } \ $の運動方程式は近似的に次のように表される。ただし$ \ v_{\theta } \ $の大きさは十分小さく，$ \ \left| v_{z0}\right| ≫\left| v_{\theta }\right| \ $とする。
\[
\begin{eqnarray}
m\frac {\mathrm {d}v_{\theta }}{\mathrm {d}t}&=&F_{1}　・・・・・・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] $ \ F_{1} \ $が$ \ z＞0 \ $の限られた微小区間$ \ \mathit {\Delta }z \ $でのみ作用すると近似すると，力が作用する微小時間$ \ \displaystyle \mathit {\Delta } t\left( =\frac {\mathit {\Delta } z}{\left| v_{z0}\right| } \right) \ $を用いて，$ \ v_{\theta } \ $は①式より，$ \ \displaystyle v_{\theta }=\frac {F_{1}}{m}\mathit {\Delta } t \ $と表される。

さらに，$ \ v_{\theta } \ $と$ \ B_{z} \ $により，電子はローレンツ力$ \ F_{2} \ $を受ける。動径方向に沿って$ \ r \ $が大きくなる方向を正に取り，符号を含めて$ \ F_{2} \ $を式で表すと，$ \ F_{2}= \ \fbox {　（３）　} \ $と表される。本問の状況では，$ \ F_{2} \ $の符号は負であることから，結果的に電子は$ \ z \ $軸に近づく方向に力を受ける。

ニュートンの第$ \ 2 \ $法則より，速度の$ \ r \ $方向成分$ \ v_{r} \ $の運動方程式は近似的に次のように表される。ただし$ \ v_{r} \ $の大きさは十分小さく，$ \ \left| v_{z0}\right| ≫\left| v_{r}\right| \ $とする。
\[
\begin{eqnarray}
m\frac {\mathrm {d}v_{r}}{\mathrm {d}t}&=&F_{2}　・・・・・・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] $ \ F_{2} \ $も$ \ F_{1} \ $と同様に，力が作用する微小時間$ \ \displaystyle \mathit {\Delta } t\left( =\frac {\mathit {\Delta } z}{\left| v_{z0}\right| } \right) \ $を用いて，②式より，$ \ v_{r}= \ \fbox {　（４）　} \ \cdot \mathit {\Delta } t \ $と表される。力の作用後は動径方向に一定の速さ$ \ \left| v_{r}\right| \ $で$ \ z \ $軸に近づいていくので，電子が$ \ z \ $軸に交わるのは時間$ \ \displaystyle \frac {r_{0}}{\left| v_{r}\right| } \ $後である。したがって，力の作用後から$ \ z \ $軸に交わるまでに電子が$ \ z \ $軸に沿って進む距離$ \ f \ $は，$ \ f=\left| v_{z0}\right| \times \displaystyle \frac {r_{0}}{\left| v_{r}\right| } \ $と表される。$ \ r_{0} \ $が微小である場合には，$ \ k \ $を比例定数として，$ \ B_{r}=kr_{0}B_{z} \ $と表されることなどを用いると，$ \ f= \ \fbox {　（５）　} \ $となり，$ \ r_{0} \ $に依存しない式で表される。これは，円電流による磁界が電子線の集束レンズとして機能することを意味し，$ \ f \ $は焦点距離に相当する。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　-e{v_{\theta }}^{2}B_{z}　　　　　&（ロ）&　-ev_{z0}B_{r}　　　　　&（ハ）&　-ev_{z0}B_{\theta } \\[ 5pt ] &（ニ）&　-ev_{\theta }{B_{z}}^{2}　　　　　&（ホ）&　\frac {m{v_{z0}}^{2}}{ek\mathit {\Delta }z^{2}{B_{z}}^{2}}　　　　　&（ヘ）&　-\frac {v_{z0}B_{z}}{e} \\[ 5pt ] &（ト）&　\frac {F_{2}}{m}　　　　　&（チ）&　-ev_{z0}{B_{z}}^{2}　　　　　&（リ）&　-ev_{\theta }B_{z} \\[ 5pt ] &（ヌ）&　\frac {F_{1}}{m}　　　　　&（ル）&　-ev_{z0}B_{z}　　　　　　&（ヲ）&　\frac {m^{2}v_{z0}}{e^{2}k\mathit {\Delta }z{B_{z}}^{2}} \\[ 5pt ] &（ワ）&　\frac {eF_{2}}{m}　　　　　&（カ）&　\frac {m^{2}{v_{z0}}^{2}}{e^{2}k\mathit {\Delta }z^{2}{B_{z}}^{2}}　　　　　　&（ヨ）&　0 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

円電流が作る磁界中の電子の運動に関する問題です。
(5)の式変形が様々な情報を整理して解く必要があり，計算量の多い問題となります。(4)までは比較的取り組みやすい問題なので，合格点を狙うのであれば十分に選択して良い問題かと思います。

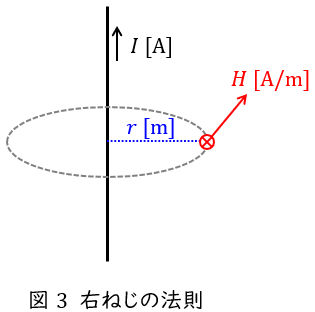
1.アンペアの周回積分の法則
電流$ \ I \ \mathrm {[A]} \ $の流れる向きに右ねじを合わせる（図3においては上向き）と，右ねじを回す向きに磁界$ \ H \ \mathrm {[A / m ]} \ $が発生し，距離$ \ r \ \mathrm {[m]} \ $離れた場所の磁界の大きさは，
\[
\begin{eqnarray}
H &=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。

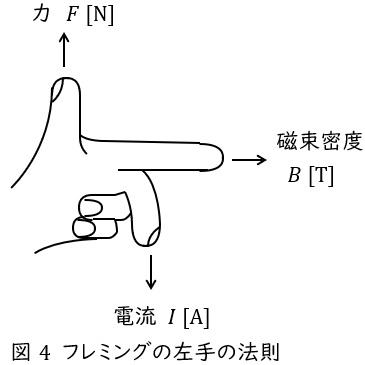
2.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ$ \ B \ \mathrm {[T]} \ $，電流の大きさ$ \ I \ \mathrm {[A]} \ $，直線状導体の長さを$ \ l \ \mathrm {[m]} \ $とすると，導体に発生する電磁力$ \ F \ \mathrm {[N]} \ $は，
\[
\begin{eqnarray}
F &=&BIl \\[ 5pt ] \end{eqnarray}
\] となります。また，真空中を電子が動いているときは，磁束密度の大きさ$ \ B \ \mathrm {[T]} \ $，電子の速度$ \ v \ \mathrm {[m / s]} \ $，電子の電荷を$ \ -e\left( e＞0 \right) \ \mathrm {[C]} \ $とすると，電子に加わるローレンツ力$ \ F \ $は
\[
\begin{eqnarray}
F &=&-evB \\[ 5pt ] \end{eqnarray}
\] となります。電子の場合，動く向きが電流の向きと逆になるので，中指の向きに注意するようにしましょう。

3.運動方程式（力学）
質量$ \ m \ \mathrm {[kg]} \ $の物体に力$ \ F \ \mathrm {[N]} \ $が加わっている時，この物体の加速度$ \ a \ \mathrm {[m / s^{2}]} \ $との間には，
\[
\begin{eqnarray}
F &=&ma \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(1)解答：ヨ
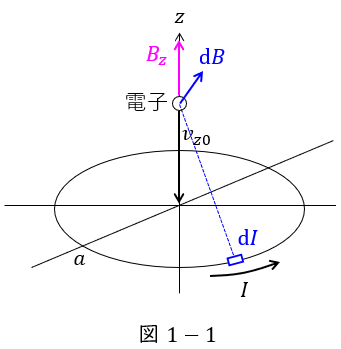
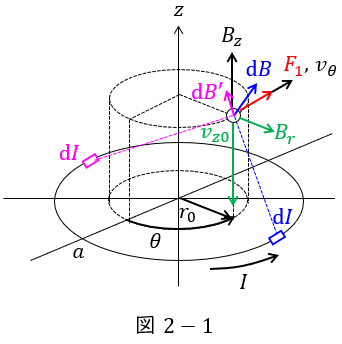
図1において，電流素片$ \ \mathrm {d}I \ $が作る磁束密度$ \ \mathrm {d}B \ $を示すと図1-1のようになり，これを円電流$ \ I \ $に沿って周回積分すると全体では大きさは$ \ B_{z} \ $のみとなる。したがって，ワンポイント解説「2.フレミングの左手の法則」の通り，電子の動く方向に対し直角成分の磁束密度がないため，電子が磁界から受けるローレンツ力の大きさは$ \ 0 \ $と求められる。

(2)解答：ロ
図2における電流素片が作る磁束密度は図2-1のようになり，反対側にある電流素片が作る磁束密度との和が零ではないため，問題文の通り$ \ B_{r} \ $が発生していることになる。
この$ \ B_{r} \ $により電子が受けるローレンツ力$ \ F_{1} \ $はフレミングの左手の法則より図2-1のようになり，その大きさは，ワンポイント解説「2.フレミングの左手の法則」の通り，
\[
\begin{eqnarray}
F_{1} &=&-ev_{z0}B_{r} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：リ
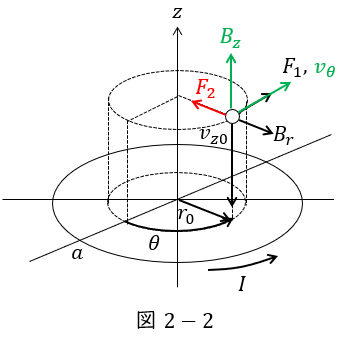
フレミングの左手の法則より，$ \ v_{\theta } \ $と$ \ B_{z} \ $により，電子が受けるローレンツ力$ \ F_{2} \ $は図2-2のようになり，その大きさは，ワンポイント解説「2.フレミングの左手の法則」の通り，
\[
\begin{eqnarray}
F_{2} &=&-ev_{\theta }B_{z} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ト
①式と同様に，②式において，力が作用する微小時間$ \ \mathit {\Delta } t \ $を用いると，
\[
\begin{eqnarray}
v_{r}&=& \frac {F_{2}}{m} \cdot \mathit {\Delta } t \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：カ
問題に与えられている式を用いて$ \ f=\left| v_{z0}\right| \times \displaystyle \frac {r_{0}}{\left| v_{r}\right| } \ $を変形していくと，
\[
\begin{eqnarray}
f&=& \left| v_{z0}\right| \times \frac {\displaystyle \frac {B_{r}}{kB_{z}}}{\displaystyle \frac {F_{2}}{m}\mathit {\Delta }t} \\[ 5pt ] &=& \frac {\displaystyle m\left| v_{z0}\right| B_{r}}{\displaystyle kB_{z}F_{2}\mathit {\Delta }t} \\[ 5pt ] &=& \frac {\displaystyle m\left| v_{z0}\right| B_{r}}{\displaystyle kB_{z}\left( -ev_{\theta }B_{z}\right) \frac {\mathit {\Delta } z}{\left| v_{z0}\right| }} \\[ 5pt ] &=& \frac {\displaystyle m{v_{z0}}^{2}B_{r}}{\displaystyle -ekv_{\theta }\mathit {\Delta } zB_{z}^{2} } \\[ 5pt ] &=& \frac {\displaystyle m{v_{z0}}^{2}B_{r}}{\displaystyle -ek\frac {F_{1}}{m}\mathit {\Delta }t\mathit {\Delta } zB_{z}^{2} } \\[ 5pt ] &=& \frac {\displaystyle m^{2}{v_{z0}}^{2}B_{r}}{\displaystyle -ekF_{1}\mathit {\Delta }t\mathit {\Delta } zB_{z}^{2} } \\[ 5pt ] &=& \frac {\displaystyle m^{2}{v_{z0}}^{2}B_{r}}{\displaystyle -ek\left( -ev_{z0}B_{r}\right) \frac {\mathit {\Delta } z}{\left| v_{z0}\right| }\mathit {\Delta } zB_{z}^{2} } \\[ 5pt ] &=& \frac {m^{2}{v_{z0}}^{2}}{e^{2}k\mathit {\Delta }z^{2}{B_{z}}^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。