《理論》〈電磁気〉[H27:問1] 誘電体中の静電界の基本性質に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，誘電体中の静電界の基本性質に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

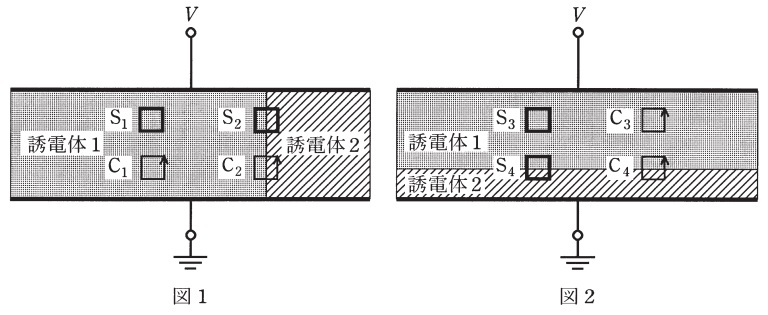
長方形の導体平板を極板とする平行平板コンデンサが二つある。このコンデンサに，異なる誘電率をもつ2種類の直方体の誘電体を，隙間のないよう，かつ極板からはみ出さないように挿入する。一つは図1のように，二つの誘電体の境界面が極板と垂直になっており，もう一つは図2のように，二つの誘電体の境界面が極板と平行になっている。共に，極板間には電位差$ \ V (≠0) \ $が与えられている。ただし，図1及び図2は横から見た図であり，端効果はないものとする。

これに対し，図1及び図2に示したように，紙面と平行に置かれた長方形の周回積分路$ \ \mathrm {C_{1}～C_{4}} \ $と，紙面と平行な面及び極板と平行な面をもつように置かれた直方体の閉曲面$ \ \mathrm {S_{1}～S_{4}} \ $を仮定する。$ \ \mathrm {C_{1}～C_{4}} \ $，$ \ \mathrm {S_{1}～S_{4}} \ $は全て誘電体内に存在し，$ \ \mathrm {C_{2}} \ $，$ \ \mathrm {C_{4}} \ $，$ \ \mathrm {S_{2}} \ $，$ \ \mathrm {S_{4}} \ $は二つの誘電体の境界面を横切っているものとする。

コンデンサ内の電界$ \ \boldsymbol E \ $，電束密度$ \ \boldsymbol D \ $と分極$ \ \boldsymbol P \ $を考える。これらの関係式は，真空の誘電率を$ \ \varepsilon _{0} \ $とすると，$ \ \fbox {　（１）　} \ $となる。また，空間内の電界のエネルギー密度は，$ \ \fbox {　（２）　} \ $で表される。

次に，$ \ \boldsymbol E \ $，$ \ \boldsymbol D \ $，$ \ \boldsymbol P \ $を長方形$ \ \mathrm {C_{1}～C_{4}} \ $でそれぞれ周回積分することを考える。このとき，$ \ \mathrm {C_{1}～C_{4}} \ $のうちの$ \ \fbox {　（３）　} \ $については，$ \ \boldsymbol D \ $と$ \ \boldsymbol P \ $の周回積分は零にならない。

今度は，$ \ \boldsymbol E \ $，$ \ \boldsymbol D \ $，$ \ \boldsymbol P \ $を直方体$ \ \mathrm {S_{1}～S_{4}} \ $でそれぞれ面積分することを考える。このとき，$ \ \mathrm {S_{1}～S_{4}} \ $のうちの$ \ \fbox {　（４）　} \ $については，$ \ \boldsymbol E \ $，$ \ \boldsymbol D \ $，$ \ \boldsymbol P \ $のうちの$ \ \fbox {　（５）　} \ $の面積分は零にならない。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　\boldsymbol Eと\boldsymbol D　　　　　&（ロ）&　\boldsymbol P=\varepsilon _{0}\boldsymbol E +\boldsymbol D　　　　　&（ハ）&　\mathrm {S_{1}とS_{3}} \\[ 5pt ] &（ニ）&　\mathrm {S_{2}}　　　　　&（ホ）&　\boldsymbol D=\varepsilon _{0}\boldsymbol E +\boldsymbol P　　　　　&（ヘ）&　\mathrm {S_{4}} \\[ 5pt ] &（ト）&　\mathrm {C_{1}とC_{3}}　　　　　&（チ）&　\boldsymbol D　　　　　&（リ）&　\mathrm {C_{4}} \\[ 5pt ] &（ヌ）&　\frac {1}{2}\boldsymbol E^{2}　　　　　&（ル）&　\mathrm {C_{2}}　　　　　&（ヲ）&　\boldsymbol D=\varepsilon _{0}\left( \boldsymbol E +\boldsymbol P\right) \\[ 5pt ] &（ワ）&　\frac {1}{2}\boldsymbol E \cdot \boldsymbol D　　　　　&（カ）&　\boldsymbol E と\boldsymbol P　　　　　&（ヨ）&　\frac {1}{2}\boldsymbol E \times \boldsymbol D
\end{eqnarray}
\]

【ワンポイント解説】

分極$ \ \boldsymbol P \ $がなければ標準的な問題ですが，分極が加わることにより，やや難しい問題となっています。電験のテキストにはあまり書いてありませんが，電磁気学の教科書には記載があると思いますので確認してみて下さい。

1.電束密度$ \ \boldsymbol D \ $と電界$ \ \boldsymbol E \ $の関係
電界により誘電体で分極$ \ \boldsymbol P \ $が起こるとき，電極感受率を$ \ \chi \ $，電界$ \ \boldsymbol E \ $とすると，
\[
\boldsymbol P≒\chi \boldsymbol E
\] となり，電束密度$ \ \boldsymbol D \ $と電界$ \ \boldsymbol E \ $の関係は，
\[
\begin{eqnarray}
\boldsymbol D &=& \varepsilon \boldsymbol E \\[ 5pt ] &=& \left( \varepsilon _{0}+\chi \right) \boldsymbol E \\[ 5pt ] &=& \varepsilon _{0}\boldsymbol E +\boldsymbol P
\end{eqnarray}
\] となります。

2.エネルギー密度$ \ w \ $
極板間の電界が$ \ \boldsymbol E \ $，電束密度が$ \ \boldsymbol D \ $であるとき，エネルギー密度$ \ w \ $は，
\[
w=\frac {1}{2}\boldsymbol E\cdot \boldsymbol D
\] となります。

【関連する「電気の神髄」記事】

　　平行平板コンデンサの静電容量まとめ

【解答】

(1)解答：ホ
ワンポイント解説「1.電束密度$ \ \boldsymbol D \ $と電界$ \ \boldsymbol E \ $の関係」より，
\[
\boldsymbol D=\varepsilon \boldsymbol E +\boldsymbol P
\] となります。

(2)解答：ワ
ワンポイント解説「2.エネルギー密度$ \ w \ $」より，
\[
w=\frac {1}{2}\boldsymbol E\cdot \boldsymbol D
\] となります。

(3)解答：ル
図1の誘電体1と誘電体2において，電界$ \ \boldsymbol E \ $は等しいが，電束密度$ \ \boldsymbol D \ $と分極$ \ \boldsymbol P \ $は異なる。また，図2の誘電体1と誘電体2において，電束密度$ \ \boldsymbol D \ $は等しいが，電界$ \ \boldsymbol E \ $と分極$ \ \boldsymbol P \ $は異なる。
$ \ \mathrm {C_{1}} \ $と$ \ \mathrm {C_{3}} \ $に関しては，長方形がすべて誘電体1の中にあるので，周回積分は零となる。
$ \ \mathrm {C_{2}} \ $に関しては，図の左の辺と右の辺の$ \ \boldsymbol E \ $は同じであるが，$ \ \boldsymbol D \ $と$ \ \boldsymbol P \ $が異なる。
$ \ \mathrm {C_{4}} \ $に関しては，図の上の辺と下の辺の$ \ \boldsymbol D \ $は同じであるが，$ \ \boldsymbol E \ $と$ \ \boldsymbol P \ $が異なる。
よって，$ \ \boldsymbol D \ $と$ \ \boldsymbol P \ $の周回積分は零にならないのは，$ \ \mathrm {C_{2}} \ $となる。

(4)解答：ヘ
(5)解答：カ
周回積分の場合と同様に直方体の上面と下面の値が異なるのは$ \ \mathrm {S_{4}} \ $の場合であり，この時，値が異なるのは$ \ \boldsymbol E \ $と$ \ \boldsymbol P \ $となる。