《機械》〈照明〉[H20:問6]屋外作業場の平均照度や投光器の所要台数に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

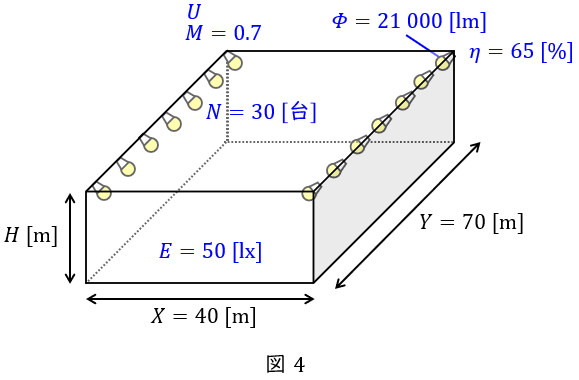
屋外作業場\( \ 40 \ \mathrm {[m]} \times 70 \ \mathrm {[m]} \ \)を，蛍光水銀ランプ\( \ 400 \ \mathrm {[W]} \ \)（ランプ光束\( \ 21 \ 000 \ \mathrm {[lm]} \ \)）を用いた投光器\( \ 30 \ \)台で照明し，平均照度\( \ 50 \ \mathrm {[lx]} \ \)を得ている。ただし，このときの保守率は\( \ 0.70 \ \)，投光器の器具効率は\( \ 65 \ \mathrm {[％]} \ \)であった。これに関して次の(1)から(4)の値を求め，記述用紙の解答欄に記入しなさい（計算根拠を明示すること）。

(1)　この屋外作業場の照明率（光束の利用率）を求めよ。ただし，答は小数点以下\( \ 3 \ \)けた目を四捨五入とする。

(2)　屋外作業場外へ漏れる光束は，総ランプ光束の何\( \ \mathrm {[％]} \ \)か。ただし，答は小数点以下を四捨五入とする。

(3)　投光器を新しいものに改修し，ランプも高効率のメタルハライドランプ（ランプ光束\( \ 40 \ 000 \ \mathrm {[lm]} \ \)）に交換すれば，照明率が\( \ 0.38 \ \)に高くなる。この改修案において，\( \ 30 \ \)台で照明した場合の平均照度（初期値）\( \ \mathrm {[lx]} \ \)を求めよ。ただし，答は小数点以下を四捨五入とする。

(4)　上記(3)において，平均照度\( \ 50 \ \mathrm {[lx]} \ \)を維持したい場合の投光器の所要台数を求めよ。ただし，保守率は\( \ 0.70 \ \)とし，また，答は小数点以下を切り上げた正の整数とする。

【ワンポイント解説】

屋外作業場の平均照度を求める問題です。
(2)が最も難易度が高い問題なので，合格のためにはそれ以外の空欄を間違えないことが重要かと思います。
くれぐれも計算ミスのないように注意して下さい。

1.光束\( \ F \ \)
光源から出る可視光の量（エネルギー）で，単位は\( \ \mathrm {[lm]} \ \)となります。
電磁気の分野の電束に似たようなイメージで良いです。

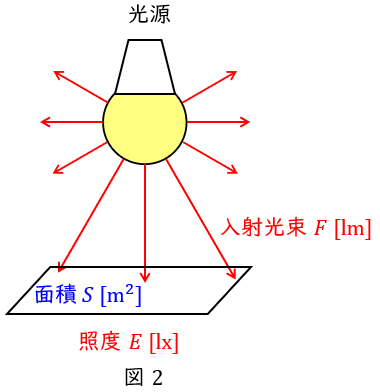
2.照度\( \ E \ \)
図2のように，面積\( \ S \ \mathrm {[m^{2}]} \ \)に入射する光束が\( \ F \ \mathrm {[lm]} \ \)であるとき，照度\( \ E \ \mathrm {[lx]} \ \)は，
\[
\begin{eqnarray}
E&=&\frac {F}{S} \\[ 5pt ] \end{eqnarray}
\] で求められます。

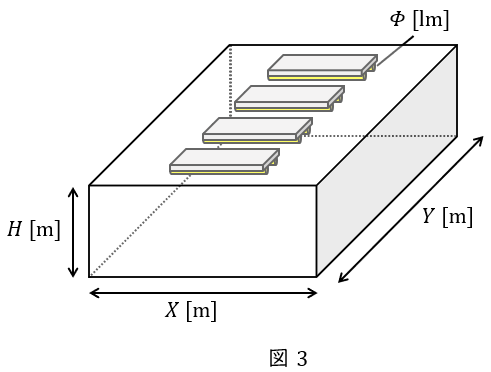
3.光束法による平均照度\( \ E \ \)の計算
間口\( \ X \ \mathrm {[m]} \ \)，奥行\( \ Y \ \mathrm {[m]} \ \)の部屋において，光源１個あたりの光束を\( \ \mathit {\Phi} \ \mathrm {[lm]} \ \)，光源の個数を\( \ N \ \mathrm {[個]} \ \)とすると，空間内の全光束\( \ F \ \mathrm {[lm]} \ \)は，
\[
\begin{eqnarray}
F&=&\mathit {\Phi}N \\[ 5pt ] \end{eqnarray}
\] となり，照明率（光源の光束が作業面に届く割合）を\( \ U \ \)，保守率（新設時の平均照度を\( \ 1 \ \)としたときの一定期間使用した後の平均照度）を\( \ M \ \)とすると，照射面積は\( \ XY \ \mathrm {[m^{2}]} \ \)なので，平均照度\( \ E \ \mathrm {[lx]} \ \)は，
\[
\begin{eqnarray}
E&=&\frac {FUM}{XY} \\[ 5pt ] &=&\frac {\mathit {\Phi} NUM}{XY} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(1)解答：\( \ 0.32 \ \)
題意に沿って図を描くと図4のようになる。平均照度\( \ E=50 \ \mathrm {[lx]} \ \)を得る式より照明率\( \ U \ \)は，ワンポイント解説「3.光束法による平均照度\( \ E \ \)の計算」の通り，
\[
\begin{eqnarray}
E&=&\frac {\mathit {\Phi} NUM}{XY} \\[ 5pt ] U&=&\frac {EXY}{\mathit {\Phi} NM} \\[ 5pt ] &=&\frac {50\times 40\times 70}{21 \ 000\times 30 \times 0.7} \\[ 5pt ] &≒&0.317 \ 5　→　0.32 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：\( \ 33 \ \mathrm {％} \ \)
投光器から発生する全光束\( \ F_{0} \ \mathrm {[lm]} \ \)は，
\[
\begin{eqnarray}
F_{0}&=&\mathit {\Phi}N \\[ 5pt ] &=&21 \ 000\times 30 \\[ 5pt ] &=&630 \ 000 \ \mathrm {[lm]} \\[ 5pt ] \end{eqnarray}
\] であり，投光器の器具効率は\( \ \eta =65 \ \mathrm {[％]} \ \)であるから，投光器から放射させる全光束\( \ F_{1} \ \mathrm {[lm]} \ \)は，
\[
\begin{eqnarray}
F_{1}&=&F_{0}\eta \\[ 5pt ] &=&630 \ 000 \times 0.65 \\[ 5pt ] &=&409 \ 500 \ \mathrm {[lm]} \\[ 5pt ] \end{eqnarray}
\] である。一方，床面に入射する光束\( \ F \ \mathrm {[lm]} \ \)は，ワンポイント解説「2.照度\( \ E \ \)」の通り，
\[
\begin{eqnarray}
F&=&EXY \\[ 5pt ] &=&50\times 40\times 70 \\[ 5pt ] &=&140 \ 000 \ \mathrm {[lm]} \\[ 5pt ] \end{eqnarray}
\] となるので，屋外作業場外へ漏れる光束\( \ F^{\prime } \ \mathrm {[lm]} \ \)とすると，床面に到達する光束との関係から，
\[
\begin{eqnarray}
F&=&\left( F_{1}-F^{\prime }\right) U \\[ 5pt ] 140 \ 000&=&\left( 409 \ 500-F^{\prime }\right) \times 0.7 \\[ 5pt ] 409 \ 500-F^{\prime }&=&200 \ 000 \\[ 5pt ] F^{\prime }&=&209 \ 500 \ \mathrm {[lm]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，屋外作業場外へ漏れる光束の割合\( \ ％F^{\prime } \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％F^{\prime }&=&\frac {F^{\prime }}{F_{0}}\times 100 \\[ 5pt ] &=&\frac {209 \ 500}{630 \ 000}\times 100 \\[ 5pt ] &≒&33.25　→　33 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

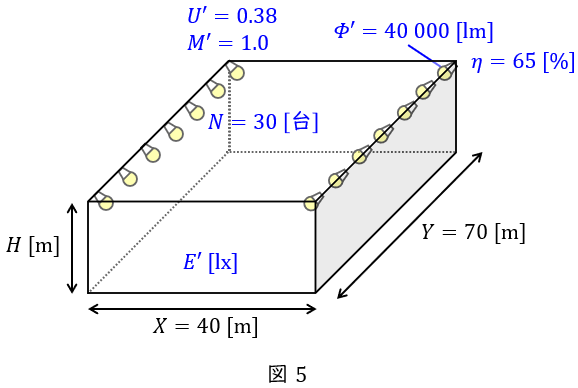
(3)解答：\( \ 163 \ \mathrm {lx} \ \)
改修案において，初期値の保守率\( \ M^{\prime }=1.0 \ \)とすれば良いから，\( \ 30 \ \)台で照明した場合の平均照度\( \ E^{\prime } \ \mathrm {[lx]} \ \)は，
\[
\begin{eqnarray}
E^{\prime }&=&\frac {\mathit {\Phi}^{\prime } NU^{\prime }M^{\prime }}{XY} \\[ 5pt ] &=&\frac {40 \ 000\times 30\times 0.38\times 1.0}{40\times 70} \\[ 5pt ] &≒&162.86　→　163 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：\( \ 14 \ \)台
保守率\( \ M^{\prime \prime }=0.7 \ \)平均照度\( \ E^{\prime \prime }=50 \ \mathrm {[lx]} \ \)を維持するときの投光器の台数を\( \ N^{\prime \prime } \ \)台とすると，平均照度を求める関係より，
\[
\begin{eqnarray}
E^{\prime \prime }&=&\frac {\mathit {\Phi}^{\prime } N^{\prime \prime }U^{\prime }M^{\prime \prime }}{XY} \\[ 5pt ] N^{\prime \prime }&=&\frac {E^{\prime \prime }XY}{\mathit {\Phi}^{\prime } U^{\prime }M^{\prime \prime }} \\[ 5pt ] &=&\frac {50\times 40\times 70}{40 \ 000 \times 0.38\times 0.7} \\[ 5pt ] &≒&13.2　→　14 \ \mathrm {[台]} \\[ 5pt ] \end{eqnarray}
\] と求められる。