《理論》〈電磁気〉[R07:問2]無限長直線電荷が作る電界と電位に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，誘導起電力によって正方形コイルに生じる誘導電流に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

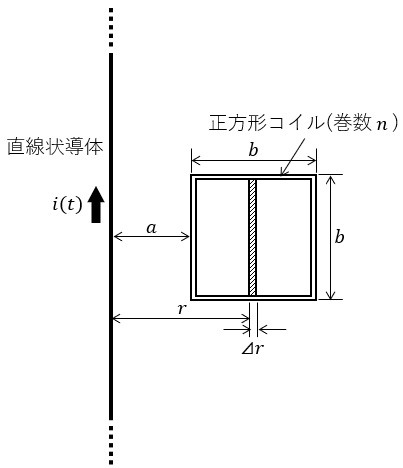
図のように，透磁率$ \ \mu _{0} \ $の空間の同一平面上に，一辺の長さ$ \ b \ $，巻数$ \ n \ $の正方形コイルと無限に長い直線状導体とが置かれている。正方形コイルの導体及び直線状導体の太さは無視でき，正方形コイルの一辺は直線状導体に平行で，距離$ \ a \ $だけ離れている。時刻$ \ t=0 \ $において直線状導体及び正方形コイルには電流は流れていない。

$ \ 0≦ t≦ t_{1} \ $において，直線状導体に流れる電流$ \ i(t) \ $を$ \ 0 \ $から$ \ I_{0} \ $に一定の割合で増加させた。$ \ t=t_{1} \ $において，$ \ i(t) \ $によって直線状導体から距離$ \ r \ $の位置に生じる磁界の大きさは$ \ \fbox {　（１）　} \ $，この位置で長さ$ \ b \ $，幅$ \ \mathit {\Delta }r \ $の面（図中のハッチング部）を貫く磁束の大きさは$ \ \fbox {　（２）　} \ $と表される。したがって，$ \ i(t) \ $が正方形コイル内につくる磁束の大きさは，$ \ 0≦ t≦ t_{1} \ $において$ \ 0 \ $から$ \ \fbox {　（３）　} \ $まで増加する。この間，正方形コイルに生じる誘導起電力の大きさは$ \ \fbox {　（４）　} \ $となる。正方形コイルが短絡されている場合，誘導起電力によって誘導電流が流れ，その際に正方形コイルに働く力の向きは$ \ \fbox {　（５）　} \ $である。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {n^{2}\mu _{0} I_{0}b}{2\pi t_{1}}\ln \left( \frac {a+b}{a}\right)　　　　　&（ロ）&　\frac {n\mu _{0} I_{0}b}{2\pi r}\mathit {\Delta }r　　　　　&（ハ）&　\frac {n\mu _{0} I_{0}b}{2\pi }\ln \left( \frac {a+b}{a}\right) \\[ 5pt ] &（ニ）&　\frac {\mu _{0} I_{0}b}{2\pi }\ln \left( \frac {a+b}{a}\right)　　　　　&（ホ）&　\frac {I_{0}}{2\pi r}　　　　　&（ヘ）&　\frac {I_{0}}{2\pi r^{2}} \\[ 5pt ] &（ト）&　\frac {I_{0}}{\pi r}　　　　　&（チ）&　\frac {\mu _{0} I_{0}b}{2\pi r}\mathit {\Delta }r　　　　　　　&（リ）&　\frac {n\mu _{0} I_{0}b}{2\pi t_{1}}\ln \left( \frac {a+b}{a}\right) \\[ 5pt ] &（ヌ）&　\frac {n\mu _{0} I_{0}b}{\pi t_{1}}\ln \left( \frac {b}{a}\right)　　　　　&（ル）&　\frac {\mu _{0} I_{0}b}{\pi r}\mathit {\Delta }r　　　　　　&（ヲ）&　\frac {\mu _{0} I_{0}b}{\pi }\ln \left( \frac {b}{a}\right) \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&（ワ）&　直線状導体と引き合う向き \\[ 5pt ] &（カ）&　直線状導体と反発し合う向き \\[ 5pt ] &（ヨ）&　直線状導体を中心軸として回転する向き \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

直線状導体と正方形コイル間の電磁誘導に関する問題です。
引っ掛けの要素もあるため難易度は普通としていますが，$ \ 1 \ $種の受験生ですと完答してくる方も多い問題かと思います。
一つ一つの原理をしっかりと理解して，ミスをしないように解いていって下さい。

1.アンペア（アンペール）の周回積分の法則
空間上の磁界ベクトルを$ \ \boldsymbol H \ $，$ \ \mathrm {C} \ $を閉曲線，$ \ \mathrm {d}\boldsymbol l \ $を$ \ \mathrm {C} \ $上の微小区間ベクトル，$ \ I \ $を$ \ \mathrm {C} \ $と鎖交する電流の総量とすると，
\[
\begin{eqnarray}
\oint_{\mathrm {C}} \boldsymbol H \cdot \mathrm {d}\boldsymbol l &=&I　 \\[ 5pt ] \end{eqnarray}
\] の関係があり，これをアンペアの周回積分の法則といいます。
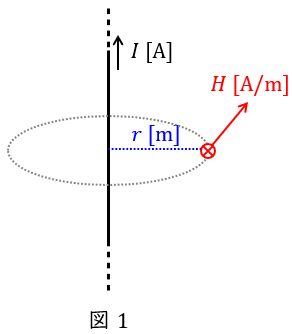
例えば，図1のように無限長直線電流$ \ I \ \mathrm {[A]} \ $が流れているとき，電線から距離$ \ r \ \mathrm {[m]} \ $の位置での磁界の強さ$ \ H \ \mathrm {[A / m]} \ $は，$ \ l=2\pi r \ $なので，
\[
\begin{eqnarray}
2\pi r H&=&I \\[ 5pt ] H&=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。

2.磁束密度$ \ B \ $
単位面積あたりに通過する磁束のことで，微小な面積$ \ \mathrm {d}\boldsymbol S \ $を通過する磁束が$ \ \mathrm {d}\mathit {\Phi } \ $であるとき，磁束密度$ \ \boldsymbol B \ $との関係は，
\[
\begin{eqnarray}
\mathrm {d}\mathit {\Phi }&=&\boldsymbol B\cdot \mathrm {d}\boldsymbol S \\[ 5pt ] \mathit {\Phi }&=&\int_{\mathrm {S}} \boldsymbol B\cdot \mathrm {d}\boldsymbol S \\[ 5pt ] \end{eqnarray}
\] となります。

3.磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係
透磁率が$ \ \mu \ \mathrm {[H / m]} \ $の時，磁束密度$ \ B \ \mathrm {[T]} \ $と磁界の大きさ$ \ H \ \mathrm {[A / m]} \ $の関係は，
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ] \end{eqnarray}
\] となります。

4.ファラデーの電磁誘導の法則と自己インダクタンス$ \ L \ $
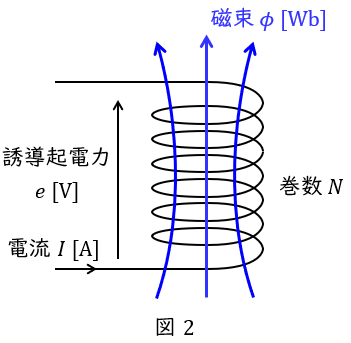
図2において，巻数$ \ N \ $のコイルを貫通する磁束$ \ \phi \ \mathrm {[Wb]} \ $があるとき，ファラデーの電磁誘導の法則より，コイルに発生する誘導起電力$ \ e \ \mathrm {[V]} \ $は，磁束の時間変化に比例し，
\[
\begin{eqnarray}
e&=&−N\frac {\mathrm {d}\phi }{\mathrm {d}t} \\[ 5pt ] \end{eqnarray}
\] で求められます。これをファラデーの電磁誘導の法則といいます。このとき，電流変化によりコイル内の磁束が変化したと考えれば，
\[
\begin{eqnarray}
e&=&−L\frac {\mathrm {d}I }{\mathrm {d}t} \\[ 5pt ] \end{eqnarray}
\] という関係も成り立ち，$ \ L \ \mathrm {[H]} \ $を自己インダクタンスと言います。これらの関係から，
\[
\begin{eqnarray}
−N\frac {\mathrm {d}\phi }{\mathrm {d}t}&=&−L\frac {\mathrm {d}I }{\mathrm {d}t} \\[ 5pt ] N\phi &=&LI \\[ 5pt ] \end{eqnarray}
\] の関係があります。

5.平行直線状導体間に働く力の大きさ
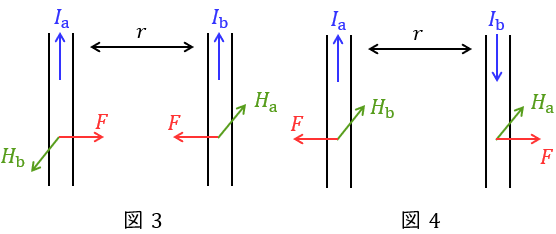
図3のような同方向に電流が流れている場合を考えます。電流$ \ I_{\mathrm {b}} \ \mathrm {[A]} \ $により発生する電流$ \ I_{\mathrm {a}} \ \mathrm {[A]} \ $が流れる導体部分の磁界の大きさ$ \ H_{\mathrm {b}} \ \mathrm {[A/m]} \ $は，アンペールの法則より，
\[
\begin{eqnarray}
H_{\mathrm {b}}&=&\frac {I_{\mathrm {b}}}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となり，空間の透磁率が$ \ \mu \ \mathrm {[H/m]} \ $であるとすると，磁束密度$ \ B_{\mathrm {b}} \ \mathrm {[T]} \ $は，
\[
\begin{eqnarray}
B_{\mathrm {b}}&=&\mu H_{\mathrm {b}} \\[ 5pt ] &=&\frac {\mu I_{\mathrm {b}}}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。フレミングの左手の法則により，$ \ I_{\mathrm {a}} \ \mathrm {[A]} \ $の流れる導体にかかる力の大きさは引力となり，その$ \ 1 \ \mathrm {[m]} \ $あたりの大きさ$ \ F \ \mathrm {[N]} \ $は，
\[
\begin{eqnarray}
F&=&B_{\mathrm {b}} I_{\mathrm {a}}\times 1 \\[ 5pt ] &=&\frac {\mu I_{\mathrm {a}}I_{\mathrm {b}}}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] と求められます。同様に$ \ I_{\mathrm {b}} \ \mathrm {[A]} \ $側や図4のような反対向きの場合も求めることができます。

【解答】

(1)解答：ホ
時刻$ \ t=t_{1} \ $において，$ \ i(t) =I_{0} \ $であるから，直線状導体から距離$ \ r \ $の位置に生じる磁界の大きさ$ \ H_{\mathrm {r}} \ $は，ワンポイント解説「1.アンペア（アンペール）の周回積分の法則」の通り，
\[
\begin{eqnarray}
H_{\mathrm {r}}&=&\frac {I_{0}}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：チ
直線状導体から距離$ \ r \ $の位置に生じる磁束密度の大きさ$ \ B_{\mathrm {r}} \ $は，ワンポイント解説「3.磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係」の通り，
\[
\begin{eqnarray}
B_{\mathrm {r}}&=&\mu _{0}H_{\mathrm {r}} \\[ 5pt ] &=&\frac {\mu _{0}I_{0}}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となるので，長さ$ \ b \ $，幅$ \ \mathit {\Delta }r \ $の面を貫く磁束の大きさ$ \ \mathit {\Phi }_{\mathrm {r}} \ $は，ワンポイント解説「2.磁束密度$ \ B \ $」の通り，
\[
\begin{eqnarray}
\mathit {\Phi }_{\mathrm {r}}&=&B_{\mathrm {r}}\cdot b\mathit {\Delta }r \\[ 5pt ] &=&\frac {\mu _{0} I_{0}b}{2\pi r}\mathit {\Delta }r \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ニ
(2)解答式において，正方形コイル内を貫く磁束$ \ \mathit {\Phi } \ $は，$ \ r \ $が$ \ a \ $から$ \ a+b \ $まで変化したときの合計であるから，
\[
\begin{eqnarray}
\mathit {\Phi }&=&\int _{a}^{a+b}\frac {\mu _{0} I_{0}b}{2\pi r}\mathrm {d}r \\[ 5pt ] &=&\frac {\mu _{0} I_{0}b}{2\pi }\int _{a}^{a+b}\frac {1}{r}\mathrm {d}r \\[ 5pt ] &=&\frac {\mu _{0} I_{0}b}{2\pi }\left[ \ln r \right] _{a}^{a+b} \\[ 5pt ] &=&\frac {\mu _{0} I_{0}b}{2\pi }\left\{ \ln \left( a+b\right) -\ln a \right\} \\[ 5pt ] &=&\frac {\mu _{0} I_{0}b}{2\pi }\ln \left( \frac {a+b}{a}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：リ
題意より，電流$ \ i(t) \ $は$ \ 0 \ $から$ \ I_{0} \ $に一定の割合で増加しているので，これに比例する磁束$ \ \mathit {\Phi } \ $も一定の割合で増加する。したがって，磁束の変化（傾き）$ \ \displaystyle \frac {\mathrm {d}\mathit {\Phi } }{\mathrm {d}t} \ $は，
\[
\begin{eqnarray}
\frac {\mathrm {d}\mathit {\Phi } }{\mathrm {d}t}&=&\frac {\mathit {\Phi }}{t_{1}} \\[ 5pt ] &=&\frac {\mu _{0} I_{0}b}{2\pi t_{1}}\ln \left( \frac {a+b}{a}\right) \\[ 5pt ] \end{eqnarray}
\] となるから，誘導起電力の大きさ$ \ e \ $は，ワンポイント解説「4.ファラデーの電磁誘導の法則と自己インダクタンス$ \ L \ $」の通り，
\[
\begin{eqnarray}
e&=&n\frac {\mathrm {d}\mathit {\Phi } }{\mathrm {d}t} \\[ 5pt ] &=&\frac {n\mu _{0} I_{0}b}{2\pi t_{1}}\ln \left( \frac {a+b}{a}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：カ
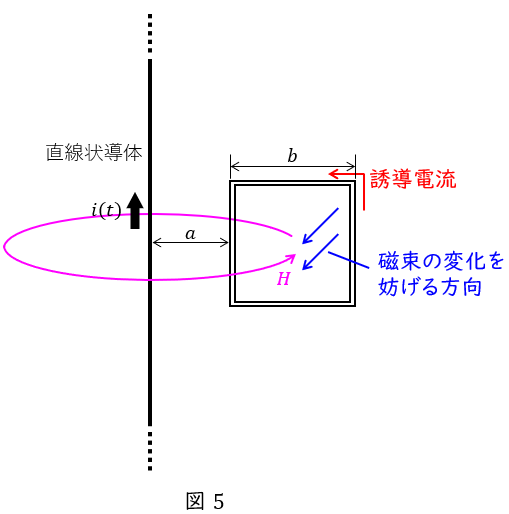
図5に示すように，直線状導体による磁界$ \ H \ $は右ねじの法則から図5のようになり，その磁束の変化を妨げる方向に誘導電流が流れるため，誘導電流の流れる向きは左回りの向きとなる。
ワンポイント解説「5.平行直線状導体間に働く力の大きさ」の通り，直線状導体から$ \ a \ $離れた平行導体には反発力，$ \ a+b \ $離れた平行導体には引力が働き，全体としては反発力の方が大きくなるため，正方形コイルに働く力の向きは直線状導体と反発し合う向きと求められる。