《理論》〈電子回路〉[H30:問7] ウィーンブリッジ発振回路に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，ウィーンブリッジ発振回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。ただし，図中の\( \ \mathrm {A} \ \)は電圧利得\( \ A \ \)倍の増幅回路である。その入力インピーダンスは無限大，出力インピーダンスは零，入出力の位相差はないものとする。

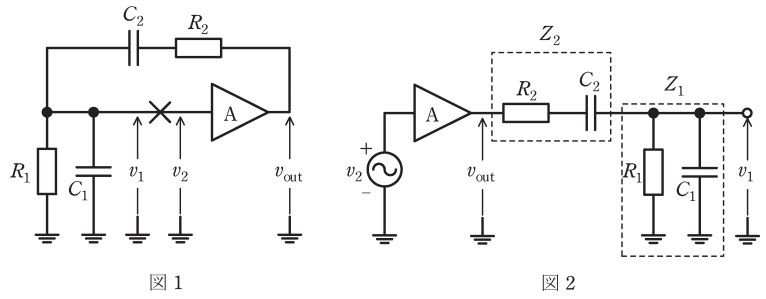
図1の発振回路を×印で示した位置で切り開き，切り開いた位置の右側に電圧源\( \ v _{2} \ \)を接続した回路が図2である。図2中の\( \ R_{1} \ \)と\( \ C_{1} \ \)の並列接続のインピーダンスを\( \ Z_{1} \ \)とすると，\( \ Z_{1} \ \)は入力電圧\( \ v _{2} \ \)の角周波数\( \ \omega \ \)を用いて\( \ \fbox {　 （１） 　} \ \)と表される。一方，\( \ R_{2} \ \)と\( \ C_{2} \ \)の直列接続のインピーダンス\( \ Z_{2} \ \)は\( \ \displaystyle R_{2}-\mathrm {j}\frac {1}{\omega C_{2}} \ \)となる。\( \ v _{1} \ \)は\( \ v _{\mathrm {out}}=Av_{2} \ \)を\( \ Z_{1} \ \)と\( \ Z_{2} \ \)とで分圧した電圧であることから，\( \ \displaystyle \frac {v_{1}}{v_{2}} \ \)は\( \ \fbox {　 （２） 　} \ \)と求められる。この\( \ \displaystyle \frac {v_{1}}{v_{2}} \ \)が図1の発振回路の一巡伝達関数である。回路は，一巡伝達関数の虚部が零となる角周波数で発振する(発振条件の周波数条件)ことから，図1の発振回路の発振角周波数は\( \ \fbox {　 （３） 　} \ \)となる。また，回路が発振状態を持続するためには発振周波数において，一巡伝達関数の実部が\( \ 1 \ \)以上(発振条件の電力条件)を満たさなければならないため，増幅回路の電圧利得\( \ A \ \)は\( \ \fbox {　 （４） 　} \ \)でなければならない。\( \ R_{1}=R_{2}=R \ \)及び\( \ C_{1}=C_{2}=C \ \)であるとき，演算増幅器を含む回路\( \ \fbox {　 （５） 　} \ \)は，\( \ \fbox {　 （４） 　} \ \)の条件を満たす増幅回路\( \ \mathrm {A} \ \)として使用することができる。ただし，演算増幅器は理想的であるとする。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {1}{R_{1}+\mathrm {j}\omega C_{1}}　　　&（ロ）&　\frac {R_{1}A}{\displaystyle \left( R_{1}+R_{2}+\frac {C_{1}}{C_{2}}R_{1}\right) +\mathrm {j} \left( \omega C_{1}R_{1}R_{2}-\frac {1}{\omega C_{2}}\right) } \\[ 5pt ] &（ハ）&　A≧1+R_{1}R_{2}　　　&（ニ）&　A≧1 \\[ 5pt ] &（ホ）&　\frac {\mathrm {j}\omega C_{1}R_{1}}{R_{1}+\mathrm {j}\omega C_{1}}　　　&（ヘ）&　\frac {\mathrm {j}\omega C_{1}R_{1}A}{\displaystyle \left( R_{1}R_{2}+\frac {C_{1}}{C_{2}}\right) +\mathrm {j} \left( \frac {R_{1}}{\omega C_{2}}+\omega C_{1}R_{1}+\omega C_{1}R_{2}\right) } \\[ 5pt ] &（ト）&　\frac {1}{\sqrt {C_{1}C_{2}R_{1}R_{2}}}　　　&（チ）&　\frac {R_{1}}{1+\mathrm {j}\omega C_{1}R_{1}} \\[ 5pt ] &（リ）&　\sqrt {\frac {R_{1}}{C_{1}C_{2}R_{2}}}　　　&（ヌ）&　\sqrt {\frac {R_{1}}{C_{1}C_{2}\left( R_{1}+R_{2}\right) }} \\[ 5pt ] &（ル）&　A≧1+\frac {R_{1}}{R_{2}}+\frac {C_{1}}{C_{2}}　　　&（ヲ）&　\frac {A}{\displaystyle \left( 1+R_{1}R_{2}\right) +\mathrm {j} \left( \omega C_{1}R_{2}-\frac {R_{1}}{\omega C_{2}}\right) } \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

(5)以外は基本的な問題であると言えると思います。(5)が分からなくても３択で当たる可能性があるので，問題として問６よりもこちらの問題を選択した方が良いかもしれません。

1.理想的なオペアンプの特徴
１．電圧増幅率が無限大です。したがって，無限大でない有限数が出力される時，入力端子間の電圧は\(0 \ \mathrm {V}\)(バーチャルショート)となります。
２．入力インピーダンスが無限大です。したがって入力端子に電流は流れません。
３．出力インピーダンスがゼロです。

【関連する「電気の神髄」記事】

　　静電容量測定用ブリッジ回路まとめ

【解答】

(1)解答：チ
図2中の\( \ R_{1} \ \)と\( \ C_{1} \ \)の並列接続のアドミタンスを\( \ Y_{1} \ \)とすると，
\[
\begin{eqnarray}
Y_{1} &=& \frac {1}{R_{1}}+\mathrm {j}\omega C_{1} \\[ 5pt ] &=& \frac {1+\mathrm {j}\omega C_{1}R_{1}}{R_{1}} \\[ 5pt ] \end{eqnarray}
\] であり，インピーダンスはアドミタンスの逆数であるから，
\[
\begin{eqnarray}
Z_{1} &=& \frac {1}{Y_{1}} \\[ 5pt ] &=& \frac {R_{1}}{1+\mathrm {j}\omega C_{1}R_{1}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ロ
分圧の法則より，
\[
\begin{eqnarray}
v_{1} &=& \frac {Z_{1}}{Z_{1}+Z_{2}}v_{\mathrm {out}} \\[ 5pt ] &=& \frac {Z_{1}}{Z_{1}+Z_{2}}Av_{2} \\[ 5pt ] \frac {v_{1}}{v_{2}} &=& \frac {Z_{1}}{Z_{1}+Z_{2}}A \\[ 5pt ] &=& \frac {\displaystyle \frac {R_{1}}{1+\mathrm {j}\omega C_{1}R_{1}}}{\displaystyle \frac {R_{1}}{1+\mathrm {j}\omega C_{1}R_{1}}+R_{2}-\mathrm {j}\frac {1}{\omega C_{2}}}A \\[ 5pt ] &=& \frac {R_{1}A}{\displaystyle R_{1}+\left( R_{2}-\mathrm {j}\frac {1}{\omega C_{2}}\right) \left( 1+\mathrm {j}\omega C_{1}R_{1}\right) } \\[ 5pt ] &=& \frac {R_{1}A}{\displaystyle \left( R_{1}+R_{2}+\frac {C_{1}}{C_{2}}R_{1}\right) +\mathrm {j} \left( \omega C_{1}R_{1}R_{2}-\frac {1}{\omega C_{2}}\right) } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ト
(2)の虚部が零となるには，
\[
\begin{eqnarray}
\omega C_{1}R_{1}R_{2}-\frac {1}{\omega C_{2}} &=& 0 \\[ 5pt ] \end{eqnarray}
\] となれば良い。\( \ \omega \ \)について整理すると，
\[
\begin{eqnarray}
\omega C_{1}R_{1}R_{2} &=& \frac {1}{\omega C_{2}} \\[ 5pt ] \omega ^{2}&=& \frac {1}{C_{1}C_{2}R_{1}R_{2} } \\[ 5pt ] \omega &=& \frac {1}{\sqrt {C_{1}C_{2}R_{1}R_{2}} } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ル
発振周波数(虚部が零)の時，一巡伝達関数の実部が\( \ 1 \ \)以上であるから，
\[
\begin{eqnarray}
\frac {R_{1}A}{\displaystyle R_{1}+R_{2}+\frac {C_{1}}{C_{2}}R_{1}}&≧& 1 \\[ 5pt ] R_{1}A&≧& R_{1}+R_{2}+\frac {C_{1}}{C_{2}}R_{1} \\[ 5pt ] A&≧& 1+\frac {R_{2}}{R_{1}}+\frac {C_{1}}{C_{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

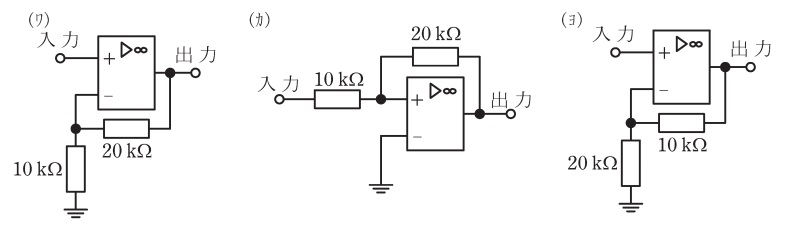
(5)解答：ワ
\( \ R_{1}=R_{2}=R \ \)及び\( \ C_{1}=C_{2}=C \ \)である時，一巡伝達関数の実部が\( \ 1 \ \)以上(発振条件の電力条件)である条件は，
\[
\begin{eqnarray}
A&≧& 1+\frac {R}{R}+\frac {C}{C} \\[ 5pt ] A&≧& 3 \\[ 5pt ] \end{eqnarray}
\] である。これを満たす回路を(ワ)～(ヨ)の中から見つける。

各図の入力電圧を\( \ v_{\mathrm {in}} \ \)，出力電圧を\( \ v_{\mathrm {out}} \ \)とする。
(ワ)の回路について，オペアンプの入力端子間の電圧差はないので，入力端子の電圧はともに\( \ v_{\mathrm {in}} \ \)となる。
また，オペアンプの入力端子には電流が流れないので，入力端子の－側の電圧\(( = \ v_{\mathrm {in}} \ )\)は，分圧の法則より，
\[
\begin{eqnarray}
v_{\mathrm {in}} &=& \frac {10\times 10^{3}}{10\times 10^{3}+20\times 10^{3}}v_{\mathrm {out}} \\[ 5pt ] &=& \frac {1}{3}v_{\mathrm {out}} \\[ 5pt ] \end{eqnarray}
\] となり，電圧増幅率は，
\[
\begin{eqnarray}
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} &=& 3 \\[ 5pt ] \end{eqnarray}
\] と求められ，\( \ A≧3 \ \)の条件を満たすこととなる。

(カ)の回路について，オペアンプの各入力端子の電圧は\( \ 0 \ \)であるので，\( 10 \ \mathrm {k\Omega } \ \)の抵抗に流れる電流\( \ I \ \)は，
\[
\begin{eqnarray}
I &=& \frac {v_{\mathrm {in}}}{10\times 10^{3}} \\[ 5pt ] \end{eqnarray}
\] となる。オペアンプの入力端子には電流が流れないので，電流\( \ I \ \)はそのまま\( 20 \ \mathrm {k\Omega } \ \)の抵抗に流れる。したがって，出力電圧及び電圧増幅率は，
\[
\begin{eqnarray}
v_{\mathrm {out}} &=& 0-20\times 10^{3}I \\[ 5pt ] &=& -20\times 10^{3}\cdot \frac {v_{\mathrm {in}}}{10\times 10^{3}} \\[ 5pt ] &=& -2v_{\mathrm {in}} \\[ 5pt ] \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}&=& -2 \\[ 5pt ] \end{eqnarray}
\] となり，\( \ A≧3 \ \)の条件を満たさない。

(ヨ)の回路について，オペアンプの入力端子間の電圧差はないので，入力端子の電圧はともに\( \ v_{\mathrm {in}} \ \)となる。
また，オペアンプの入力端子には電流が流れないので，入力端子の－側の電圧\(( = \ v_{\mathrm {in}} \ )\)は，分圧の法則より，
\[
\begin{eqnarray}
v_{\mathrm {in}} &=& \frac {20\times 10^{3}}{20\times 10^{3}+10\times 10^{3}}v_{\mathrm {out}} \\[ 5pt ] &=& \frac {2}{3}v_{\mathrm {out}} \\[ 5pt ] \end{eqnarray}
\] となり，電圧増幅率は，
\[
\begin{eqnarray}
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} &=& \frac {3}{2} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ A≧3 \ \)の条件を満たさない。
以上から，\( \ A≧3 \ \)の条件を満たすのは(ワ)となる。