【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,真空中の静電界に関する諸法則の微分形に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
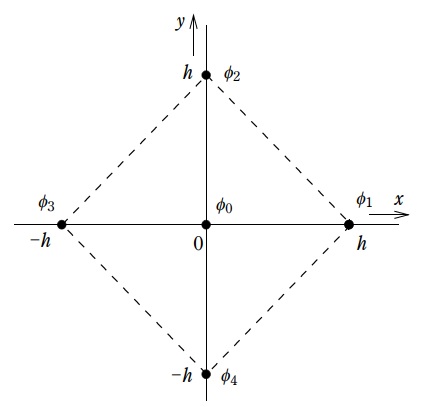
図のように,直交座標系において電界の\( \ z \ \)軸成分が零となるような電界について,\( \ xy \ \)平面の二次元で電位や電界を考える。ここで,\( \ 4 \ \)点\( \ ( h,0 ) \ \),\( \ ( 0,h ) \ \),\( \ ( -h,0 ) \ \),\( \ ( 0,-h ) \ \)の電位がそれぞれ\( \ \mathit {\phi }_{1} \ \),\( \ \mathit {\phi }_{2} \ \),\( \ \mathit {\phi }_{3} \ \),\( \ \mathit {\phi }_{4} \ \)であり,\( \ 4 \ \)点を頂点とする正方形の内側には電荷が存在せず,その電位\( \ \mathit {\phi } \ \)が次式のような二次関数で表されるとする。
\[
\begin{eqnarray}
\mathit {\phi } ( x,y ) &=& ax^{2}+bxy+cy^{2}+dx+ey+f ・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
電界\( \ \boldsymbol E=( E_{\mathrm {x}},E_{\mathrm {y}},0 ) \ \)は\( \ \boldsymbol E=-\mathrm {grad}\mathit {\phi } ( x,y ) \ \)で計算できる。このとき,電界\( \ \boldsymbol E \ \)について,電界の保存性を表す式より,\( \ \fbox { (1) } \ \)が常に成り立つ。
また,\( \ \fbox { (2) } \ \)の法則を微分形で記述すると,電荷が存在しないため,次式となる。
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol E &=& \fbox { (3) } &=& 0 \\[ 5pt ]
\end{eqnarray}
\]
この式から導かれる\( \ a ~ f \ \)の関係式は,
\[
\begin{eqnarray}
\fbox { (4) } ・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
である。
また,①式から原点の電位は,\( \ \mathit {\phi }_{0}=\mathit {\phi } ( 0,0 ) =f \ \)で与えられる。そこで,\( \ 4 \ \)点の座標と電位\( \ \mathit {\phi }_{1} ~ \mathit {\phi }_{4} \ \)を①式に代入し,②式の関係を考慮して,\( \ f \ \)を\( \ \mathit {\phi }_{1} ~ \mathit {\phi }_{4} \ \)を用いて表せば,\( \ \mathit {\phi }_{0}=f=\fbox { (5) } \ \)となる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \mathrm {rot}\boldsymbol E =0 &(ロ)& a+c=0 &(ハ)& \frac {\mathit {\phi }_{1}+\mathit {\phi }_{2}+\mathit {\phi }_{3}+\mathit {\phi }_{4}}{4} \\[ 5pt ]
&(ニ)& \frac { \partial E_{\mathrm {y}}}{ \partial x }-\frac { \partial E_{\mathrm {x}}}{ \partial y } &(ホ)& d+e=0 &(ヘ)& b^{2}=4ac \\[ 5pt ]
&(ト)& \frac { \partial E_{\mathrm {y}}}{ \partial x }+\frac { \partial E_{\mathrm {x}}}{ \partial y } &(チ)& \frac { \partial E_{\mathrm {x}}}{ \partial x }+\frac { \partial E_{\mathrm {y}}}{ \partial y } &(リ)& \frac {\mathit {\phi }_{1}\mathit {\phi }_{3}-\mathit {\phi }_{2}\mathit {\phi }_{4}}{\mathit {\phi }_{1}+\mathit {\phi }_{2}+\mathit {\phi }_{3}+\mathit {\phi }_{4}} \\[ 5pt ]
&(ヌ)& ガウス &(ル)& \boldsymbol E =0 &(ヲ)& アンペール \\[ 5pt ]
&(ワ)& \frac {\mathit {\phi }_{1}+\mathit {\phi }_{2}-\mathit {\phi }_{3}-\mathit {\phi }_{4}}{2} &(カ)& クーロン &(ヨ)& \boldsymbol E =\left( \frac {\mathit {\phi }_{1}-\mathit {\phi }_{2}}{h},\frac {\mathit {\phi }_{3}-\mathit {\phi }_{4}}{h},0\right)
\end{eqnarray}
\]
【ワンポイント解説】
マクスウェルの方程式を使ったやや高度な問題です。\( \ \boldsymbol E=-\mathrm {grad}\mathit {\phi } ( x,y ) \ \)等は大学の電磁気の教科書に出てくる内容で,典型的な1種らしい問題とも言えると思います。深追いすると電験の範囲を逸脱するレベルになるので,ご興味のある方は電磁気学の専門書を見て下さい。
1.\( \ \mathrm {rot} \ \)(回転)
\( \ \mathrm {rot} \ \)の定義は,
\[
\begin{eqnarray}
\mathrm {rot} \boldsymbol E&=&\left( \frac { \partial E_{\mathrm {z}}}{ \partial y }-\frac { \partial E_{\mathrm {y}}}{ \partial z },\frac { \partial E_{\mathrm {x}}}{ \partial z }-\frac { \partial E_{\mathrm {z}}}{ \partial x },\frac { \partial E_{\mathrm {y}}}{ \partial x }-\frac { \partial E_{\mathrm {x}}}{ \partial y }\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,外積を用いて表すと,
\[
\begin{eqnarray}
\mathrm {rot} \boldsymbol E &=& \begin{bmatrix} \mathrm {i} & \mathrm {j} & \mathrm {k} \\ \frac { \partial }{ \partial x } & \frac { \partial }{ \partial y } & \frac { \partial }{ \partial z } \\ E_{\mathrm {x}} & E_{\mathrm {y}} & E_{\mathrm {z}} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となり,こちらの方が覚えやすいと思います。
(\( \ \mathrm {i} \ \),\( \ \mathrm {j} \ \),\( \ \mathrm {k} \ \)は\( \ x \ \)軸,\( \ y \ \)軸,\( \ z \ \)軸の単位ベクトルです)
2.\( \ \mathrm {div} \ \)(発散)
ある微小な立方体の発散量で次式で定義されます。
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol E &=& \frac { \partial E_{\mathrm {x}}}{ \partial x }+\frac { \partial E_{\mathrm {y}}}{ \partial y }+\frac { \partial E_{\mathrm {z}}}{ \partial z } \\[ 5pt ]
\end{eqnarray}
\]
3.\( \ \mathrm {grad} \ \)(勾配)
勾配という意味で,電磁気では電界\( \ E \ \)が電位\( \ V \ \)の傾きとなります。
\[
\begin{eqnarray}
\boldsymbol E &=& -\mathrm {grad} V \\[ 5pt ]
&=& \left( -\frac { \partial V}{ \partial x },-\frac { \partial V}{ \partial y },-\frac { \partial V}{ \partial z }\right) \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:イ
ワンポイント解説「3.\( \ \mathrm {grad} \ \)(勾配)」より,
\[
\begin{eqnarray}
\boldsymbol E &=& -\mathrm {grad} \mathit {\phi } ( x,y ) \\[ 5pt ]
&=& \left( -2ax-by-d,-bx-2cy-e,0\right) ・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
であるので,ワンポイント解説「1.\( \ \mathrm {rot} \ \)(回転)」より,
\[
\begin{eqnarray}
\mathrm {rot} \boldsymbol E&=&\left( \frac { \partial E_{\mathrm {z}}}{ \partial y }-\frac { \partial E_{\mathrm {y}}}{ \partial z },\frac { \partial E_{\mathrm {x}}}{ \partial z }-\frac { \partial E_{\mathrm {z}}}{ \partial x },\frac { \partial E_{\mathrm {y}}}{ \partial x }-\frac { \partial E_{\mathrm {x}}}{ \partial y }\right) \\[ 5pt ]
&=&\left( 0-0,0-0,-b+b\right) \\[ 5pt ]
&=&\left( 0,0,0\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \mathrm {rot }\boldsymbol E =0 \ \)が常に成り立つ。
※電界の保存性より正確に求めるならば,ストークスの定理\( \ \int _{\mathrm {c}}\boldsymbol E \mathrm {d}\boldsymbol l =\int _{\mathrm {s}}\mathrm {rot }\boldsymbol E \mathrm {d}\boldsymbol S =0\ \)を使用することが必要です。\( \ \mathrm {rot }\boldsymbol E =0 \ \)は電磁気の教科書には掲載されているので,興味のある方は確認してみて下さい。
(2)解答:ヌ
静電界で用いられる法則はガウスの法則となります。ガウスの法則の微分形は電荷密度\( \ \rho \ \)を用いて,
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol E&=&\frac {\rho }{\varepsilon _{0}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
(3)解答:チ
ワンポイント解説「2.\( \ \mathrm {div} \ \)(発散)」より,
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol E &=& \frac { \partial E_{\mathrm {x}}}{ \partial x }+\frac { \partial E_{\mathrm {y}}}{ \partial y }+\frac { \partial E_{\mathrm {z}}}{ \partial z } \\[ 5pt ]
&=& \frac { \partial E_{\mathrm {x}}}{ \partial x }+\frac { \partial E_{\mathrm {y}}}{ \partial y } \\[ 5pt ]
\end{eqnarray}
\]
となる。
(4)解答:ロ
③式より,
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol E &=& \frac { \partial E_{\mathrm {x}}}{ \partial x }+\frac { \partial E_{\mathrm {y}}}{ \partial y } \\[ 5pt ]
&=& -2a-2c \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \mathrm {div} \boldsymbol E =0 \ \)より,
\[
\begin{eqnarray}
-2a-2c &=& 0 \\[ 5pt ]
a+c&=& 0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ハ
\( \ \mathit {\phi }_{1} \ \),\( \ \mathit {\phi }_{2} \ \),\( \ \mathit {\phi }_{3} \ \),\( \ \mathit {\phi }_{4} \ \)の電位は,
\[
\begin{eqnarray}
\mathit {\phi }_{1} &=& \mathit {\phi } ( h,0 ) \\[ 5pt ]
&=& ah^{2}+dh+f \\[ 5pt ]
\mathit {\phi }_{2} &=& \mathit {\phi } ( 0,h ) \\[ 5pt ]
&=& ch^{2}+eh+f \\[ 5pt ]
\mathit {\phi }_{3} &=& \mathit {\phi } ( -h,0 ) \\[ 5pt ]
&=& ah^{2}-dh+f \\[ 5pt ]
\mathit {\phi }_{4} &=& \mathit {\phi } ( 0,-h ) \\[ 5pt ]
&=& ch^{2}-eh+f \\[ 5pt ]
\end{eqnarray}
\]
となり,それぞれ足し合わせると,
\[
\begin{eqnarray}
\mathit {\phi }_{1}+\mathit {\phi }_{2}+\mathit {\phi }_{3}+\mathit {\phi }_{4} &=& \left( ah^{2}+dh+f\right) +\left( ch^{2}+eh+f \right) +\left( ah^{2}-dh+f\right) +\left( ch^{2}-eh+f\right) \\[ 5pt ]
&=& \left( 2a+2c\right) h^{2}+4f \\[ 5pt ]
\end{eqnarray}
\]
となり,(4)の解答式より,
\[
\begin{eqnarray}
\mathit {\phi }_{1}+\mathit {\phi }_{2}+\mathit {\phi }_{3}+\mathit {\phi }_{4} &=& 4f \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,
\[
\begin{eqnarray}
\mathit {\phi }_{0}&=& f \\[ 5pt ]
&=& \frac {\mathit {\phi }_{1}+\mathit {\phi }_{2}+\mathit {\phi }_{3}+\mathit {\phi }_{4}}{4} \\[ 5pt ]
\end{eqnarray}
\]
が成立する。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん