【問題】
【難易度】★★★★☆(やや難しい)
図1に示すような,三相定格回路電圧\( \ 6 \ 600 \ \mathrm {[V]} \ \),定格周波数\( \ 50 \ \mathrm {[Hz]} \ \),同一定格の単相缶形コンデンサ\( \ 3 \ \)台を三角結線した三相定格設備容量\( \ 1 \ 500 \ \mathrm {[kvar]} \ \),直列リアクトル\( \ 6 \ \mathrm {[%]} \ \)を有する進相設備\( \ 6 \ \)組がある。
この進相設備\( \ 6 \ \)組の缶形コンデンサ合計\( \ 18 \ \)台を用いて,図2に示すように,三相星形結線で一相分を缶形コンデンサ\( \ 2 \ \)直列・\( \ 3 \ \)並列接続で構成した,三相定格回路電圧\( \ 22 \ \mathrm {[kV]} \ \),定格周波数\( \ 50 \ \mathrm {[Hz]} \ \)で直列リアクトル\( \ 6 \ \mathrm {[%]} \ \)の進相設備を設計する。
この場合,定格回路電圧\( \ 6 \ 600 \ \mathrm {[V]} \ \)で使用していた直列リアクトル及び放電コイルは\( \ 22 \ \mathrm {[kV]} \ \)回路では使用できないので,新規に製作するものとする。
これらの条件で,次の問に答えよ。
(1) コンデンサ設備に使用される放電抵抗と放電コイルの違いを構造や機能面から説明せよ。
(2) 定格回路電圧\( \ 6 \ 600 \ \mathrm {[V]} \ \)で使用しているときの単相缶形コンデンサの定格電圧\( \ U_{C0} \ \mathrm {[V]} \ \)と缶形コンデンサ\( \ 1 \ \)台当たりの定格容量\( \ Q_{C0} \ \mathrm {[kvar]} \ \)及び\( \ 22 \ \mathrm {[kV]} \ \)回路で使用する場合のコンデンサ群一相分(\( \ 2 \ \)直列\( \ 3 \ \)並列構成)の定格相電圧\( \ U_{C} \ \mathrm {[V]} \ \)を求めよ。
(3) \( \ 22 \ \mathrm {[kV]} \ \)回路で得られるコンデンサの三相定格容量\( \ Q_{C22} \ \mathrm {[kvar]} \ \),必要となる直列リアクトルの定格容量\( \ Q_{L} \ \mathrm {[kvar]} \ \)及び定格進相設備容量\( \ Q \ \mathrm {[kvar]} \ \)を求めよ。


【ワンポイント解説】
直列リアクトルと放電コイルを接続した進相コンデンサに関する問題です。
内容自体は一度は学習したことがあるような範囲からの出題ですが,\( \ \Delta \ \)結線や\( \ \mathrm {Y} \ \)結線を組み合わせたり,電圧を変えたりすることで受験生を迷わせる問題です。ミスを非常にしやすい問題なので,落ち着いて解いていくようにして下さい。
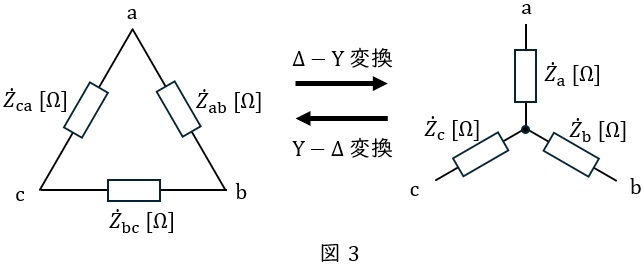
1.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
図3において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
②\( \ \mathrm {Y}-\Delta \ \)変換
図3において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
平衡三相回路においては,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}&=&{\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
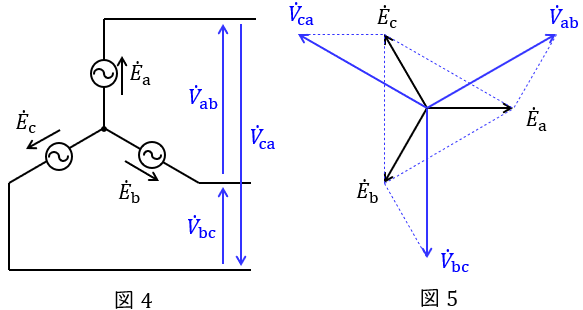
2.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
図4のような三相対称電源がある時,線間電圧と相電圧の関係は図5のベクトル図のようになり,線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると,
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ]
V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ]
V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \left( 30^{\circ } \right) \ \)進みであることが分かります。
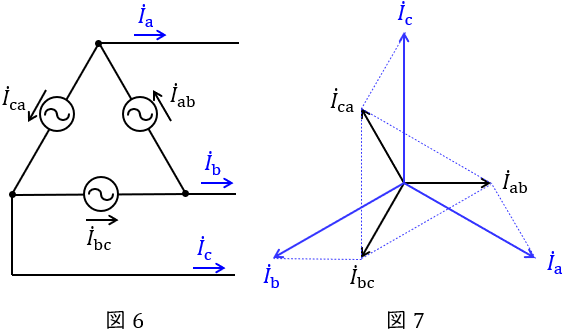
3.\( \ \Delta \ \)結線における相電流と線電流の関係
図6のような三相対称電源がある時,線電流と相電流の関係は図7のベクトル図のようになり,線電流の大きさは相電流の大きさと比較すると,
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\sqrt {3}I_{\mathrm {ab}} \\[ 5pt ]
I_{\mathrm {b}} &=&\sqrt {3}I_{\mathrm {bc}} \\[ 5pt ]
I_{\mathrm {c}} &=&\sqrt {3}I_{\mathrm {ca}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \left( 30^{\circ } \right) \)遅れであることが分かります。
【解答】
(1)コンデンサ設備に使用される放電抵抗と放電コイルの違い
(ポイント)
・いずれもコンデンサを回路から切り離した際,内部に残る電荷を安全に放電させる素子です。
・放電抵抗が\( \ 5 \ \)分以内に\( \ 50 \ \mathrm {[V]} \ \)以下に放電させるのに対し,放電コイルは遥かに小さい\( \ 5 \ \)秒以内に\( \ 50 \ \mathrm {[V]} \ \)以下に放電させることができます。
・コンデンサ設備を再投入する際に\( \ 5 \ \)分待機していなければならないのは,設備として大きなデメリットとなるため,放電コイルを設けます。
(試験センター解答例)
放電抵抗:
コンデンサの両端子間に常時接続される高抵抗の抵抗器で,電源からコンデンサが切り離された場合に残留電荷を\( \ 5 \ \)分以内に\( \ 50 \ \mathrm {[V]} \ \)以下に放電させる。
放電コイル:
コンデンサが回路から切り離された場合に残留電荷を\( \ 5 \ \)秒以内に\( \ 50 \ \mathrm {[V]} \ \)以下に放電させる。鉄心にコイルを巻いた構造で,交流電源に接続されているときは高インピーダンスであるが,残留電荷の直流で励磁されると鉄心が飽和し,急速にインピーダンスが低下することで残留電荷を放電させる。
(2)単相缶形コンデンサの定格電圧\( \ U_{C0} \ \mathrm {[V]} \ \)と\( \ 1 \ \)台当たりの定格容量\( \ Q_{C0} \ \mathrm {[kvar]} \ \)及びコンデンサ群一相分(\( \ 2 \ \)直列\( \ 3 \ \)並列構成)の定格相電圧\( \ U_{C} \ \mathrm {[V]} \ \)
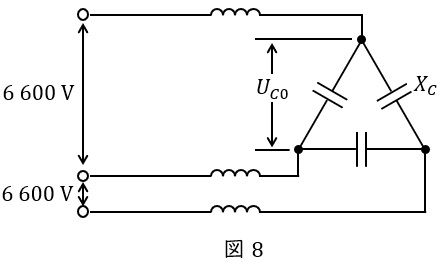
コンデンサのリアクタンスを\( \ X_{C} \ \mathrm {[\Omega ]} \ \)とすると,放電コイルを無視すれば図1の回路は図8のようになり,さらに\( \ \Delta -\mathrm {Y} \ \)変換すると,図9のようになる。
図9より,単相缶形コンデンサの定格電圧\( \ U_{C0} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
\frac {U_{C0}}{\sqrt {3}} &=&\frac {{X_{C}}^{\prime }}{{X_{C}}^{\prime }-X_{L}}\times \frac {6 \ 600}{\sqrt {3}} \\[ 5pt ]
U_{C0} &=&\frac {{X_{C}}^{\prime }}{{X_{C}}^{\prime }-0.06{X_{C}}^{\prime }}\times 6 \ 600 \\[ 5pt ]
&=&\frac {1}{1-0.06}\times 6 \ 600 \\[ 5pt ]
&≒&7 \ 021.3 → 7 \ 020 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
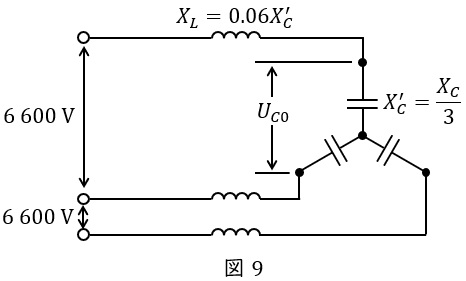
三相定格設備容量が\( \ 1 \ 500 \ \mathrm {[kvar]} \ \)なので,一相あたりの定格設備容量は\( \ 500 \ \mathrm {[kvar]} \ \)となり,図9より線電流を\( \ I \ \mathrm {[A]} \ \)とすれば,
\[
\begin{eqnarray}
500\times 10^{3} &=&\left( {X_{C}}^{\prime }-X_{L}\right) I^{2} \\[ 5pt ]
&=&\left( {X_{C}}^{\prime }-0.06{X_{C}}^{\prime }\right) I^{2} \\[ 5pt ]
&=&0.94{X_{C}}^{\prime } I^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,図9より\( \ Q_{C0}={X_{C}}^{\prime } I^{2} \ \)なので,
\[
\begin{eqnarray}
500\times 10^{3}&=&0.94Q_{C0} \\[ 5pt ]
Q_{C0}&=&\frac {500\times 10^{3}}{0.94} \\[ 5pt ]
&≒&531.91\times 10^{3} \ \mathrm {[var]} → 532 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
また,図2の定格相電圧\( \ U_{C} \ \mathrm {[V]} \ \)も同様に考えればよいので,
\[
\begin{eqnarray}
U_{C} &=&\frac {1}{1-0.06}\times \frac {22 \ 000}{\sqrt {3}} \\[ 5pt ]
&≒&13 \ 512 → 13 \ 500 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ 22 \ \mathrm {[kV]} \ \)回路で得られるコンデンサの三相定格容量\( \ Q_{C22} \ \mathrm {[kvar]} \ \),必要となる直列リアクトルの定格容量\( \ Q_{L} \ \mathrm {[kvar]} \ \)及び定格進相設備容量\( \ Q \ \mathrm {[kvar]} \ \)
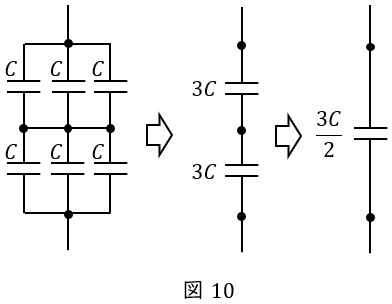
缶形コンデンサ\( \ 1 \ \)台の静電容量を\( \ C \ \mathrm {[F]} \ \)とすると,図9のように\( \ \Delta -\mathrm {Y} \ \)変換したときの静電容量は\( \ 3C \ \mathrm {[F]} \ \)となるから,
\[
\begin{eqnarray}
Q_{C0}&=&2\pi f\cdot 3C \left( \frac {U_{C0}}{\sqrt {3}} \right) ^{2} \\[ 5pt ]
&=&2\pi fC {U_{C0}} ^{2} \\[ 5pt ]
C&=&\frac {Q_{C0}}{2\pi f {U_{C0}} ^{2}} \\[ 5pt ]
&=&\frac {531.91\times 10^{3}}{2\pi \times 50\times 7 \ 021.3 ^{2}} \\[ 5pt ]
&≒&3.434 \ 4\times 10^{-5} \ \mathrm {[F]} \\[ 5pt ]
\end{eqnarray}
\]
となり,図10に示すように,\( \ 2 \ \)直列・\( \ 3 \ \)並列接続のコンデンサの静電容量は\( \ \displaystyle \frac {3}{2}C \ \)であるから,\( \ 22 \ \mathrm {[kV]} \ \)回路で得られるコンデンサの三相定格容量\( \ Q_{C22} \ \mathrm {[kvar]} \ \)は,
\[
\begin{eqnarray}
Q_{C22}&=&3\cdot 2\pi f\cdot \frac {3}{2}C U_{C} ^{2} \\[ 5pt ]
&=&9\pi fC U_{C} ^{2} \\[ 5pt ]
&=&9\pi \times 50\times 3.434 \ 4\times 10^{-5} \times 13 \ 512 ^{2} \\[ 5pt ]
&≒&8.864 \ 5\times 10^{6} \ \mathrm {[var]} → 8 \ 860 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。(2)と同様に考えれば\( \ Q=XI^{2} \ \)の関係から,容量はリアクタンスに比例するので,必要となる直列リアクトルの定格容量\( \ Q_{L} \ \mathrm {[kvar]} \ \)は,
\[
\begin{eqnarray}
Q_{L}&=&0.06Q_{C22} \\[ 5pt ]
&=&0.06\times 8.864 \ 5\times 10^{6} \\[ 5pt ]
&=&5.318 \ 7\times 10^{5} \ \mathrm {[var]} → 532 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
となり,定格進相設備容量\( \ Q \ \mathrm {[kvar]} \ \)は,
\[
\begin{eqnarray}
Q&=&Q_{C22}-Q_{L} \\[ 5pt ]
&=&8.864 \ 5\times 10^{6}-5.318 \ 7\times 10^{5} \\[ 5pt ]
&≒&8.33\times 10^{6} \ \mathrm {[var]} → 8 \ 330 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん