《機械・制御》〈変圧器〉[H29:問2]単相変圧器のV結線に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

図のように\( \ 2 \ \)台の一次定格電圧\( \ \mathrm {6600 \ V} \ \)，二次定格電圧\( \ \mathrm {200 \ V} \ \)，定格周波数\( \ \mathrm {50 \ Hz} \ \)及び定格容量\( \ \mathrm {10 \ kV\cdot A} \ \)の単相変圧器がある。変圧器\( \ \mathrm {ab} \ \)を\( \ \mathrm {a} \ \)相と\( \ \mathrm {b} \ \)相との間に，変圧器\( \ \mathrm {cb} \ \)を\( \ \mathrm {c} \ \)相と\( \ \mathrm {b} \ \)相の間に\( \ \mathrm {V} \ \)結線し，定格電圧，定格周波数の三相交流電源に接続する。次の問に答えよ。ただし，変圧器の巻線抵抗と漏れリアクタンスによる電圧降下は無視し，三相交流電源の相順は\( \ \mathrm {a} \ \)相→\( \ \mathrm {b} \ \)相→\( \ \mathrm {c} \ \)相の順とする。

(1)　図1のように平衡三相抵抗負荷を接続する。\( \ 2 \ \)台の変圧器で抵抗負荷に供給できる最大の電力を求めよ。
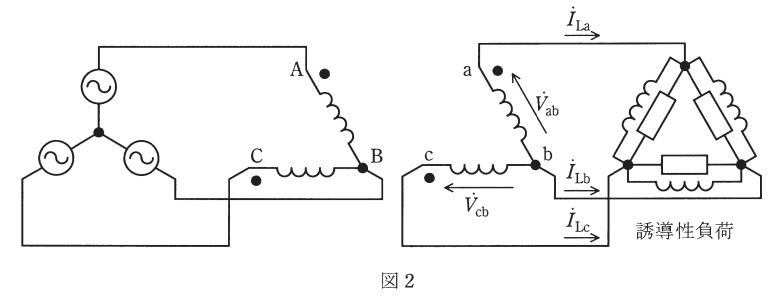
(2)　図2のように三相負荷を接続する。ただし，負荷は三相平衡であるが，誘導性で力率角\( \ \mathrm {30°} \ \)，消費電力は\( \ \mathrm {12 \ kW} \ \)である。変圧器\( \ \mathrm {ab} \ \)及び変圧器\( \ \mathrm {cb} \ \)が伝達する有効電力\(P_{\mathrm {ab}}\)及び\(P_{\mathrm {cb}}\)を求めよ。
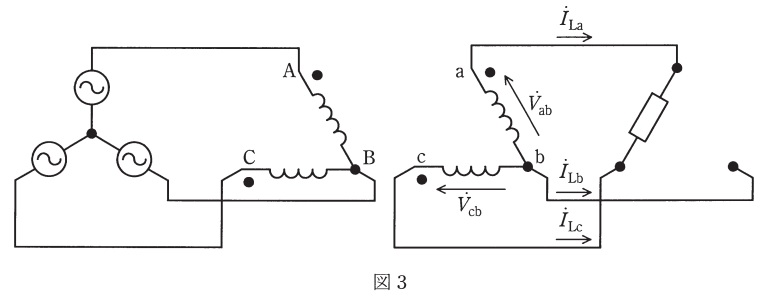
(3)　図3のように，単相負荷抵抗を二次側の\( \ \mathrm {a} \ \)相と\( \ \mathrm {c} \ \)相との間に接続する。\( \ 2 \ \)台の変圧器で抵抗負荷に供給できる最大の電力を求めよ。
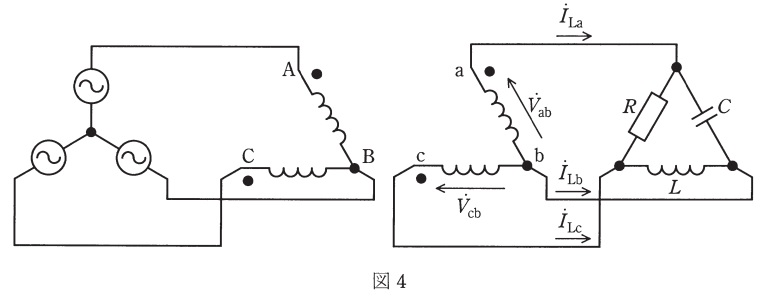
(4)　図4のように，単相抵抗負荷\( \ R \ \)に分路リアクトル\( \ L \ \)及び進相コンデンサ\( \ C \ \)を接続する。\( \ L \ \)及び\( \ C \ \)のリアクタンス\( \ X_{\mathrm {L}} \ \)及び\( \ X_{\mathrm {C}} \ \)を適切に選べば，各変圧器の電圧と電流が同位相，すなわち負荷力率を\( \ 1 \ \)に改善できる。回路の対称性から，\(X_{\mathrm {L}}=X_{\mathrm {C}}\)であるので，力率を\( \ 1 \ \)にできる\( \ X_{\mathrm {L}} \ \)又は\( \ X_{\mathrm {C}} \ \)の\( \ R \ \)に対する比\( \ \displaystyle \frac {X_{\mathrm {L}}}{R} \ \)又は\( \ \displaystyle \frac {X_{\mathrm {C}}}{R} \ \)の一方を求めよ。

【ワンポイント解説】

変圧器の\( \ \mathrm {V} \ \)結線に関する問題です。一種らしく，数字丸暗記では解くことが難しく，変圧器の性質をきちんと理解しておくことが求められます。

【解答】

(1)平衡三相抵抗負荷に供給できる最大電力
二次側の定格電流\( \ I_{\mathrm {n}} \ \)の大きさは，定格容量\( \ P_{\mathrm {n}}=\mathrm {10 \ kV\cdot A} \ \)，定格二次電圧\( \ V_{\mathrm {2n}}=\mathrm {200 \ V} \ \)より，
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{V_{\mathrm {2n}}} \\[ 5pt ] &=&\frac {10000}{200} \\[ 5pt ] &=&50 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるから，平衡三相抵抗負荷に供給できる最大電力\( \ P_{\mathrm {m1}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {m1}}&=&\sqrt {3}V_{\mathrm {2n}}I_{\mathrm {n}}\cos \theta \\[ 5pt ] &=&\sqrt {3}\times 200\times 50\times 1 \\[ 5pt ] &≒&17321 \ \mathrm {[W]}　→　17.3 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)平衡三相誘導性負荷に伝達する有効電力
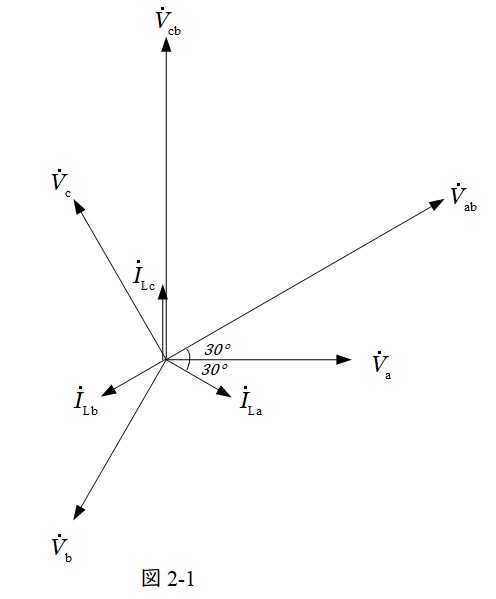
題意に沿って，\( \ \mathrm {a} \ \)点の相電圧\( \ {\dot V}_{\mathrm {a}} \ \)を基準とした各ベクトル図を描くと，図2-1のようになる。
\( \ {\dot I}_{\mathrm {La}} \ \)の大きさは，力率角\( \ \theta \ \)が\( \ \mathrm {30°} \ \)，消費電力\( \ P_{\mathrm {o}} \ \)が\( \ \mathrm {12 \ kW} \ \)であるから，
\[
\begin{eqnarray}
I_{\mathrm {La}}&=&\frac {P_{\mathrm {o}}}{\sqrt {3} V_{\mathrm {2n}} \cos \theta} \\[ 5pt ] &=&\frac {12000}{\sqrt {3}\times 200 \cos 30°} \\[ 5pt ] &=&40 \ \mathrm{[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，変圧器\( \ \mathrm {ab} \ \)が供給する有効電力\( \ P_{\mathrm {ab}} \ \)は図2-1より，\( \ V_{\mathrm {ab}} \ \)と\( \ I_{\mathrm {La}} \ \)の位相差が\( \ 60° \ \)であるので，
\[
\begin{eqnarray}
P_{\mathrm {ab}}&=&V_{\mathrm {ab}}I_{\mathrm {La}}\cos 60° \\[ 5pt ] &=&200\times 40\cos 60° \\[ 5pt ] &=&4000 \ \mathrm{[W]}　→　4.0 \ \mathrm{[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，変圧器\( \ \mathrm {cb} \ \)が供給する有効電力\( \ P_{\mathrm {cb}} \ \)は図2-1より，\( \ V_{\mathrm {cb}} \ \)と\( \ I_{\mathrm {Lc}} \ \)が同相であるので，
\[
\begin{eqnarray}
P_{\mathrm {cb}}&=&V_{\mathrm {cb}}I_{\mathrm {Lc}} \\[ 5pt ] &=&200\times 40 \\[ 5pt ] &=&8000 \ \mathrm{[W]}　→　8.0 \ \mathrm{[kW]}
\end{eqnarray}
\] と求められる。

(3)\( \ 2 \ \)台の変圧器で抵抗負荷に供給できる最大電力
(1)より，負荷へ供給できる最大電流\( \ I_{\mathrm {n}} \ \)は\( \ \mathrm {50 \ A} \ \)であるため，供給できる最大電力\( \ P_{\mathrm {m3}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {m3}}&=&V_{\mathrm {2n}}I_{\mathrm {n}} \\[ 5pt ] &=&200\times 50 \\[ 5pt ] &=&10000 \ \mathrm{[W]}　→　10.0 \ \mathrm{[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)力率を\( \ 1 \ \)にできる\( \ X_{\mathrm {L}} \ \)又は\( \ X_{\mathrm {C}} \ \)の\( \ R \ \)に対する比
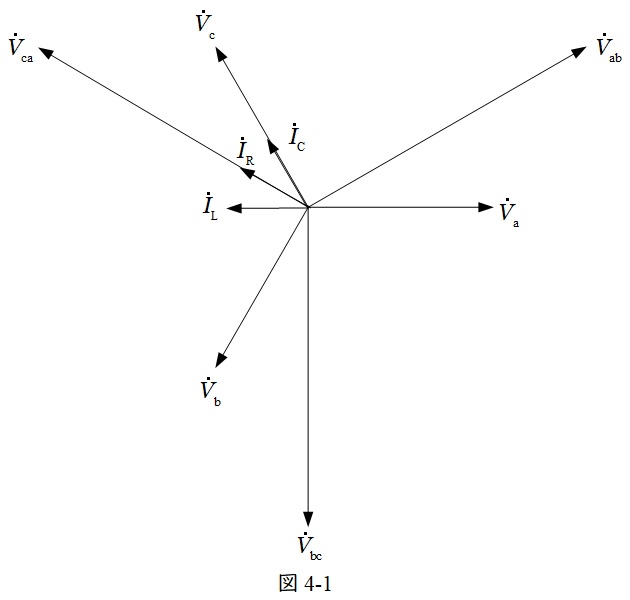
題意に沿って，コンデンサでは電流が\( \ 90° \ \)進み，リアクトルでは電流が\( \ 90° \ \)遅れになることを考慮してベクトル図を描くと図4-1のようになる。
ここで，\( \ {\dot V}_{\mathrm {a}} \ \)を基準とした時の線間電圧\( \ {\dot V}_{\mathrm {ab}} \ \)，\( \ {\dot V}_{\mathrm {bc}} \ \)，\( \ {\dot V}_{\mathrm {ca}} \ \)はそれぞれ，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {ab}}&=&200(\cos 30°+\mathrm {j}\sin 30°) \\[ 5pt ] &=&100\sqrt {3} +\mathrm {j}100 \\[ 5pt ] {\dot V}_{\mathrm {bc}}&=&200(\cos 270°+\mathrm {j}\sin 270°) \\[ 5pt ] &=&-\mathrm {j}200 \\[ 5pt ] {\dot V}_{\mathrm {ca}}&=&200(\cos 150°+\mathrm {j}\sin 150°) \\[ 5pt ] &=&-100\sqrt {3} +\mathrm {j}100 \\[ 5pt ] \end{eqnarray}
\] となるので，コンデンサ，リアクトル，抵抗にそれぞれ流れる電流\( \ {\dot I}_{\mathrm {C}} \ \)，\( \ {\dot I}_{\mathrm {L}} \ \)，\( \ {\dot I}_{\mathrm {R}} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {C}}&=&\mathrm {j}\frac {{\dot V}_{\mathrm {ab}}}{X_{\mathrm {C}}} \\[ 5pt ] &=&\frac {-100+j100\sqrt {3}}{X_{\mathrm {C}}} \\[ 5pt ] {\dot I}_{\mathrm {L}}&=&\frac {{\dot V}_{\mathrm {bc}}}{\mathrm {j}X_{\mathrm {L}}} \\[ 5pt ] &=&\frac {-200}{X_{\mathrm {L}}} \\[ 5pt ] {\dot I}_{\mathrm {R}}&=&\frac {{\dot V}_{\mathrm {ca}}}{R} \\[ 5pt ] &=&\frac {-100\sqrt {3} +\mathrm {j}100}{R} \\[ 5pt ] \end{eqnarray}
\] となる。よって，各変圧器を流れる電流\( \ {\dot I}_{\mathrm {La}} \ \)，\( \ {\dot I}_{\mathrm {Lc}} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {La}}&=&{\dot I}_{\mathrm {C}}-{\dot I}_{\mathrm {R}} \\[ 5pt ] &=&\frac {-100+\mathrm {j}100\sqrt {3}}{X_{\mathrm {C}}} -\frac {-100\sqrt {3} +\mathrm {j}100}{R} \\[ 5pt ] &=&\left( \frac {-100}{X_{\mathrm {C}}}+\frac {100\sqrt {3}}{R}\right) +\mathrm {j}\left( \frac {100\sqrt {3}}{X_{\mathrm {C}}}-\frac {100}{R}\right)
\end{eqnarray}
\] \[
\begin{eqnarray}
{\dot I}_{\mathrm {Lc}}&=&{\dot I}_{\mathrm {R}}-{\dot I}_{\mathrm {L}} \\[ 5pt ] &=&\frac {-100\sqrt {3} +\mathrm {j}100}{R}-\frac {-200}{X_{\mathrm {L}}} \\[ 5pt ] &=&\left( \frac {-100\sqrt {3}}{R}+\frac {200}{X_{\mathrm {L}}}\right) +\mathrm {j}\frac {100}{R}
\end{eqnarray}
\] となる。したがって，各変圧器の電力は，
\[
\begin{eqnarray}
P_{\mathrm {ab}}+\mathrm {j}Q_{\mathrm {ab}}&=&\overline {{\dot V}_{\mathrm {ab}}}\cdot {\dot I}_{\mathrm {La}} \\[ 5pt ] &=&\left( 100\sqrt {3} -\mathrm {j}100\right) \left[ \left( \frac {-100}{X_{\mathrm {C}}}+\frac {100\sqrt {3}}{R}\right) +\mathrm {j}\left( \frac {100\sqrt {3}}{X_{\mathrm {C}}}-\frac {100}{R}\right) \right] \\[ 5pt ] &=&20000\left[ \frac {1}{R}+\mathrm {j}\left( \frac {2}{X_{\mathrm {C}}}-\frac {\sqrt {3}}{R}\right) \right] \end{eqnarray}
\] \[
\begin{eqnarray}
P_{\mathrm {cb}}+\mathrm {j}Q_{\mathrm {cb}}&=&\overline {{\dot V}_{\mathrm {cb}}}\cdot {\dot I}_{\mathrm {Lc}} \\[ 5pt ] &=&-\mathrm {j}200 \left[ \left( \frac {-100\sqrt {3}}{R}+\frac {200}{X_{\mathrm {L}}}\right) +\mathrm {j}\frac {100}{R} \right] \\[ 5pt ] &=&20000\left[ \frac {1}{R}+\mathrm {j}\left( \frac {\sqrt {3}}{R}-\frac {2}{X_{\mathrm {L}}}\right) \right] \end{eqnarray}
\] となる。よって，力率が\( \ 1 \ \)であるためには，\( \ Q_{\mathrm {ab}} \ \)および\( \ Q_{\mathrm {cb}} \ \)が\( \ 0 \ \)となればよいので，それぞれ求めると，
\[
\begin{eqnarray}
\frac {2}{X_{\mathrm {C}}}-\frac {\sqrt {3}}{R}=0　⇔　\frac {X_{\mathrm {C}}}{R}=\frac {2}{\sqrt {3}} \\[ 5pt ] \frac {\sqrt {3}}{R}-\frac {2}{X_{\mathrm {L}}}=0　⇔　\frac {X_{\mathrm {L}}}{R}=\frac {2}{\sqrt {3}}
\end{eqnarray}
\] となる。